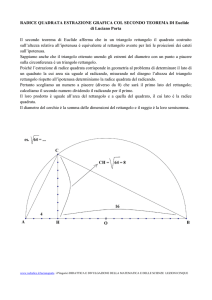
EQUIVALENZA: I TEOREMI DI
PITAGORA E DI EUCLIDE
premessa
L’attività che viene presentata in questa relazione vuole sviluppare il tema relativo
all’equivalenza tra figure piane attraverso il sussidio didattico fornito dal software Cabri.
E una attività che si interpone tra due momenti distinti all’interno del modulo di
geometria riguardante le figure piane.
Lo scopo dell’intervento è infatti duplice: da una parte si vuole consolidare gli
apprendimenti relativi all’equivalenza tra figure piane, verificando le competenze
acquisite in precedenza e dall’altra si intende introdurre i teoremi relativi ai triangoli
rettangoli di Euclide e Pitagora, andando a verificare particolari equivalenze.
Per questo motivo, l’attività si svolgerà in due tempi: durante una prima parte verrà
affrontata una costruzione guidata e poi verrà proposto un lavoro da fare a piccoli
gruppi sull’equivalenza tra figure piane, mentre nella seconda dopo una introduzione
utile per le costruzioni successive, verrà presentata una ulteriore attività da svolgere
sempre a gruppi di due, di introduzione ai teoremi principali sui triangoli rettangoli.
I tempi necessari allo sviluppo delle due fasi comprensive dei vari punti che verranno
presentato in seguito, saranno di tre lezioni di due ore ciascuna.
La scelta dell’argomento è dovuta all’opportunità fornita dal sussidio di avvicinare gli
studenti ad un concetto fondamentale della geometria spesso appreso in maniera
mnemonica, attraverso uno strumento che li costringa a imparare a ragionare,
immaginare, formulare ipotesi, e a cercare strategie per risolvere un problema. Inoltre,
sperimentando e scoprendo nuovi concetti, hanno la possibilità di acquisire nuove abilità
e competenze matematiche spendibili anche in altri contesti.
L’approccio per problemi con cui l’attività si presenta, intende sviluppare le capacità di
porsi problemi e di fare delle congetture, ma anche di astrarre generalizzare e trovare
delle dimostrazioni.
Le attività di gruppo sono proposte nell’ottica del cooperative-learning, quindi con
l’obiettivo di usufruire del confronto tra pari per migliorare l’apprendimento.
I gruppi operativi saranno possibilmente costituiti da due studenti per dare a ciascuno la
possibilità di partecipare in prima persona.
1
Perché i lavori di gruppo siano effettivamente frutto di collaborazioni, l’insegnante avrà
cura di controllare in itinere le attività dialogando e scambiando con ciascuno
impressioni, dubbi e proposte, oltre a richiedere un lavoro conclusivo individuale da
svolgere a casa.
Gli strumenti con cui si affronterà questo intervento sono costituiti, oltre che dal
software Cabri, da schede fornite agli alunni dall’insegnante, che guideranno il lavoro e
allo stesso tempo saranno utili ad una discussione finale volta a sciogliere eventuali dubbi
e difficoltà, ma anche a consolidare gli apprendimenti e all’esercizio nell’uso del
linguaggio specifico.
contesto scolastico
Questa attività può essere proposta in un qualsiasi biennio in cui si affronti un
programma di geometria: gli obiettivi e i nodi concettuali coinvolti risultano interessanti ,
in quanto fondamentali, per numerose situazioni scolastiche dove si affronta la
geometria euclidea .
prerequisiti
Per poter introdurre la prima delle due fasi dell’attività, si suppone che sia stata
affrontata la parte di geometria che dallo studio di rette parallele tagliate da una
trasversale porta ai parallelogrammi , che sia stato sviluppato il concetto di misura di
aree, di equivalenza di figure piane da cui poi ricavare l’espressione di aree delle
principali figure piane.
Si considera nota la conoscenza di base del software Cabri, nel senso che si suppone che
abbiano già provato ad usare ed esercitarsi con i comandi Punti, Rette, Curve, Verifica
proprietà, Misura, Archivi in occasioni in cui si chiedeva loro di operare con costruzioni
con riga e compasso.
obiettivi
gli obiettivi che questa attività si propone sono:
2
saper risolvere problemi con l’ausilio di un software
consolidare le conoscenze e le competenze sul concetto di equivalenza
saper verificare il teorema di Pitagora
saper distinguere le condizioni in cui tale teorema si può applicare
saper verificare il primo e il secondo teorema di Euclide
attraverso la risoluzione di problemi, saper ricostruire dalle conoscenze apprese in
precedenza, i concetti fondamentali proposti dall’attività e generalizzarli
saper lavorare ed apprendere collaborando
acquisire maggior dimestichezza col software
In generale si vogliono raggiungere degli obiettivi metacognitivi che consentano allo
studente di operare consapevolmente con i concetti sopra esposti, sviluppando delle vere
e proprie padronanze cognitive.
Lo scopo del lavoro proposto è che lo studente confermi regole e modelli, scoprendone
limiti e condizioni di validità, confrontando tra loro situazioni, favorendo processi di
analogia, di discriminazione. Con alcuni degli esercizi delle due diverse attività, viene
inoltre prospettato un ampliamento delle regole imparate, cercando di stimolare processi
cognitivi come riflettere, valutare, scegliere, immaginare, generare, intuire..
In questi processi che favoriscono l’autonomia dello studente, il sussidio didattico è
sicuramente un notevole supporto, in quanto rispetto all’approccio tradizionale stimola
la scoperta e la sperimentazione, permettendo di operare modifiche e variazioni alle
costruzioni in modo agevole e veloce.
scaletta prima lezione
presentazione dell’attività e formazione dei gruppi (15’)
richiami sull’equivalenza (5’)
presentazione di un problema col software, in modo da richiamarne l’impiego (20’)
consegna del materiale e risposte ad eventuali domande sull’attività (5’)
svolgimento dell’attività da parte degli studenti (55’)
Come introduzione al lavoro da affrontare, agli studenti viene proposta la seguente
costruzione, in modo tale da richiamare la modalità di utilizzo del software e rispondere
ad eventuali domande sull’argomento.
Trasformare un trapezio ABCD in un triangolo equivalente.
3
La sequenza del processo consisterà in:
disegnare un trapezio: l’insegnante disegna sullo schermo un trapezio ABCD con
base maggiore AB, secondo le fasi (assegnando di volta in volta il nome ai punti
individuati)
- traccia il segmento AB con segmento
- considera il punto C preso sulla retta tracciata da B con retta e traccia la
retta parallela per AB passante per C con retta parallela
- su quest’ultima prende un punto D con punto su un oggetto
- nasconde il segmento AB e la retta CD con mostra/nascondi
- traccia il trapezio con poligono
disegnare un triangolo equivalente al trapezio:
- trova il punto medio M del lato BC con punto medio
- traccia le rette DM e AB con retta e individua il loro punto di intersezione
T con intersezione di due oggetti
- dopo aver nascosto le rette disegna il triangolo ADT con triangolo
verifica dell’equivalenza: verifica che ABCD e ATD sono equivalenti,
misurandone le rispettive aree con Area.
Sarà interessante far osservare come variano le aree e come si mantiene l’equivalenza,
spostando col mouse il vertice C.
materiale per gli studenti
Le due pagine che seguono costituiscono il materiale che verrà distribuito agli studenti
prima dell’inizio dell’attività.
Comprendono non solo gli esercizi da svolgere ma anche spunti di riflessione e richiami
che dovrebbe essere utile allo svolgimento del lavoro.
C’è inoltre una parte dedicata a l’annotazione di elementi utili nella fase di discussione
che per motivi di tempo, avrà luogo la lezione successiva.
4
LABORATORIO DI MATEMATICA
Esercitazione I del __________classe _______
Nome e Cognome ____________________________________________
Nome e Cognome ____________________________________________
1. verificare che due parallelogrammi che abbiano ordinatamente congruenti basi e
altezze, sono equivalenti.
2. trasformare un triangolo assegnato qualsiasi, in uno isoscele avente la stessa base
equivalente.
3. trasformare un parallelogramma ABCD in un rombo ad esso equivalente.
4. trasformare un triangolo generico in un rombo ad esso equivalente.
Durante lo svolgimento dell’esercitazione con l’utilizzo del software Cabri, in aiuto al
procedimento risolutivo dei quesiti assegnati, completare:
a) stabilita una unità di misura, come si misura la superficie di un parallelogramma?
Perché? Come è stata ricavata tale formula?
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
b) come si definisce un triangolo isoscele? Come si calcola la superficie di un triangolo?
____________________________________________________________________
____________________________________________________________________
c) definire il rombo.
Suggerimento per lo svolgimento dell’esercizio 3) : supponendo AB>AD, traccia la retta
CD e la circonferenza con centro A e raggio AB. Considera il punto di intersezione T
con CD: tale punto forma con A e B un triangolo ABT la cui superficie rispetto ad
ABCD corrisponde a.. Si tratta di un triangolo che per costruzione è … e quindi…
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
Naturalmente non è l’unico modo possibile. Per esempio in quale altro modo lo
affronteresti?
____________________________________________________________________
____________________________________________________________________
5
____________________________________________________________________
Provare a risolvere i problemi annotando i passi principali effettuati, includendo :
- cenni sui tentavi falliti
- eventuali domande
- teoremi e definizioni usate
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
6
esame dei problemi proposti e analisi eventuali difficoltà
attività richiamate nei problemi proposti:
1. costruzioni con riga e compasso,
2. verifica di proprietà già dimostrate,
3. scoperta di nuove proprietà mediante la sperimentazione,
4. avvio alla dimostrazione.
Problema
Attività
richiamate
Probabili difficoltà
1,2
1-2
3
1-2-4
Una possibile difficoltà potrebbe verificarsi
inizialmente nell'impostare la costruzione richiesta.
Sono esercitazioni utili anche per consolidare le abilità
nell'utilizzo dello strumento.
Seguendo il suggerimento, potrebbero trovare difficoltà
nell’accorgersi che il triangolo è la metà del rombo
richiesto; una volta stabilito questo devono richiamare
le varie conoscenze sul rombo e sulle costruzioni con
riga e compasso per disegnare la figura richiesta
4
1-2-4
Anche in questo caso la criticità sta nel costruire la
figura equivalente, utilizzando le diverse conoscenze e
abilità acquisite relative al modulo trattato.
scaletta seconda lezione
Nella seconda lezione verranno ripresi i concetti affrontati la volta precedente,
esaminando la risoluzione degli esercizi proposti.
Verranno chiamati alcuni ragazzi a presentare la loro attività e si discuteranno i diversi
approcci e le difficoltà rilevate, utilizzando come guida la scheda che avevano ricevuto la
lezione precedente.
Si concedono alcuni minuti per sistemare gli esercizi incompleti o errati nello
svolgimento, per procedere poi ad introdurre l’attività successiva.
7
parte introduttiva di cui sopra (30’)
creazione di una macro (15’)
distribuzione materiale e formazione dei gruppi (5’)
seconda attività (50’)
Per realizzare le varie verifiche richieste dai problemi che seguono , è utile costruire una
macro che permetta di tracciare un quadrato di lato assegnato. Questa è anche una
occasione per introdurre un processo che può tornare utile anche in altre attività.
Lo schema che verrà seguito dall’insegnante nel condurre ogni studente a tale
costruzione, è il seguente:
- costruire un quadrato
si disegna un segmento AB con segmento ; si traccia la circonferenza di centro A
e passante per B con circonferenza e la retta per A perpendicolare ad AB con
retta perpendicolare. Si determinano i punti di intersezione di tale retta con la
circonferenza con intersezione di due oggetti e sia D quello appartenente alla
circonferenza superiore . Si traccia la retta per B perpendicolare ad AB e quella
per D perpendicolare ad AD. Denominiamo con C il punto di intersezione e
disegniamo ABCD con la casella poligono.
- creare la macro
si clicca sulla casella macro nella bara degli strumenti e poi si sceglie oggetti
iniziali e si indica con il cursore il segmento AB. Passando poi a oggetti finali si
indica col cursore il quadrato ABCD; infine si attiva definizione della macro che
mostra una finestra di dialogo, dove nel riquadro nome della costruzione
scriviamo “quadrato di lato assegnato” ; nel riquadro nome per il primo oggetto
finale scriviamo “questo quadrato”, in messaggio di aiuto invece “disegna un
quadrato di lato assegnato”. Dopo aver salvato passiamo alla verifica.
- verificare la macro
disegniamo un segmento, clicchiamo sulla casella macro nella tendina compare
anche la voce “quadrato di lato assegnato” dopo averla selezionata per il segmento
disegnato , viene tracciato il quadrato che ha per lato quel segmento.
materiale per gli studenti
I due fogli seguenti costituiranno il materiale fornito agli studenti per la seconda attività.
8
LABORATORIO DI MATEMATICA
Esercitazione II del __________classe _______
Nome e Cognome ____________________________________________
Nome e Cognome ____________________________________________
1. costruisci un triangolo rettangolo ABC di ipotenusa AB. Utilizzando la macro
“quadrato di lato assegnato”, traccia i quadrati di lati AB, BC, AC e verifica la
relazione espressa dal teorema di Pitagora.
2. costruisci un segmento AB , il suo asse a su cui prendi un punto C; costruisci ora i
quadrati su AB, BC, AC e verifica che non vale la relazione secondo cui il
quadrato su AB è equivalente alla somma degli altri quadrati costruiti su BC e AC.
Muovendo C sull’asse verifica che vale solo se l’angolo ABC è di 90° (per
misurare l’angolo usa “misura dell’angolo”della casella “misura”).
3. costruisci un triangolo rettangolo e verifica che il quadrato costruito su un cateto è
equivalente al rettangolo che ha per lati l’ipotenusa e la proiezione del cateto
sull’ipotenusa (primo teorema di Euclide).
4. costruisci un triangolo rettangolo e verifica che il quadrato costruito sull’altezza
relativa all’ipotenusa è equivalente al rettangolo che ha per lati le proiezioni dei
cateti sull’ipotenusa (secondo teorema di Euclide).
5. disegna un rettangolo ABCD e costruisci un quadrato equivalente ad esso
utilizzando il primo teorema di Euclide (N.B. : tutti i triangoli inscritti in una
semicirconferenza sono rettangoli!).
6. disegna un rettangolo ABCD e utilizza il secondo teorema di Euclide per costruire
un quadrato ad esso equivalente.
7. se sul triangolo rettangolo ABC costruiamo semicirconferenze di diametro AB,
BC, AC, e applichiamo l’equivalenza espressa dal teorema di Pitagora alle
semicirconferenze piuttosto che ai quadrati costruiti sui lati, tale relazione è ancora
verificata? E se sostituiamo i quadrati con triangoli equilateri?
Per lo svolgimento dell’esercitazione con l’utilizzo del software Cabri, in preparazione al
procedimento risolutivo dei quesiti assegnati, completare:
9
a) scrivi la relazione espressa dal teorema di Pitagora per il triangolo ABC, specificando a
quali triangoli è possibile applicarla.
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
b) scrivi le relazioni espresse dai teoremi di Euclide per il triangolo ABC rettangolo in C,
avente per base l’ipotenusa AB e per proiezione di C sull’ipotenusa, il punto H.
____________________________________________________________________
____________________________________________________________________
c)completa: il primo teorema di Euclide dice che un rettangolo le cui dimensioni
corrispondono a….è equivalente ad un quadrato il cui lato è…
____________________________________________________________________
____________________________________________________________________
d) completa: il secondo teorema di Euclide dice che un rettangolo le cui dimensioni
corrispondono a….è equivalente ad un quadrato il cui lato è…
____________________________________________________________________
____________________________________________________________________
e) come si può generalizzare il teorema di Pitagora?
____________________________________________________________________
____________________________________________________________________
Provare a risolvere i problemi annotando i passi principali effettuati, includendo :
- cenni sui tentavi falliti
- eventuali domande
- teoremi e definizioni usate
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
10
esame dei problemi proposti e analisi eventuali difficoltà
attività richiamate nei problemi proposti:
1. costruzioni con riga e compasso,
2. verifica di proprietà già dimostrate,
3. scoperta di nuove proprietà mediante la sperimentazione,
4. avvio alla dimostrazione.
Problema
Attività
richiamate
Probabili difficoltà
1,2,3,4
1-2-3-4
5,6
1-2-4
I primi quattro esercizi non presentano particolari
difficoltà: richiedono piuttosto di acquisire abilità nelle
costruzioni con riga e compasso, che in ogni caso
presuppongono competenze nell’organizzare un
processo di precise operazioni in sequenza, e scoprire
relazioni mediante sperimentazione.
Questi quesiti permettono di consolidare le conoscenze
nell’uso del software.
Potrebbero incontrare difficoltà nella costruzione
richiesta e nel riconoscere le condizioni poste dal
problema, cioè nell’impostare la figura associando le
dimensioni del rettangolo a quelle utili del triangolo di
riferimento.
7
1- 3-4
Potrebbero incontrare difficoltà nella costruzione
richiesta. Definendo nuove macro per la
semicirconferenza e per il triangolo equilatero,
verrebbe sicuramente semplificato il processo. Il
docente potrebbe decidere eventualmente di suggerire
questa ipotesi di lavoro.
11
scaletta terza lezione
completamento dell’attività iniziata la lezione precedente (50’)
correzione e discussione relativa ai temi affrontati nell’attività (35’)
formalizzazione dei concetti fondamentali interessati dal lavoro svolto (15’)
Viene dedicata alla seconda attività la prima unità didattica della terza lezione poiché si
ritiene che il tempo fornito la lezione precedente, non sia sufficiente al completo
svolgimento della stessa .
Con la collaborazione di alcuni studenti chiamati ad esporre il lavoro svolto in gruppo, e
basandosi sulle schede ricevute durante l’attività, vengono affrontate eventuali difficoltà
o dubbi riscontrati nello sviluppo del lavoro assegnato.
Vengono in particolar modo sottolineate le nuove scoperte e le sperimentazioni
effettuate dagli studenti.
L’insegnante coglie l’occasione per formalizzare alla lavagna le relazioni ottenute o
verificate durante il lavoro di gruppo: una volta rivista tutta l’attività e dopo aver
concesso del tempo per completare e sistemare gli appunti, utilizza come punto di
partenza per la lezione di geometria relativa ai teoremi di Pitagora e di Euclide, le
considerazioni raccolte durante l’ultima attività.
Come lavoro individuale da fare per casa viene assegnato il compito di riordinare sotto
forma di breve relazione scritta i punti salienti incontrati nello svolgimento delle due
attività.
12
13