somma 17 pari

Elisa Gonizzi
N° matricola: 138861
Lezione del 17-01-2002 14:30-16:30
RISOLUZIONE DI ESERCIZI IN PREPARAZIONE
ALLA PROVA SCRITTA D’ESAME
Breve premessa:
Elementi di similitudine e differenze tra:
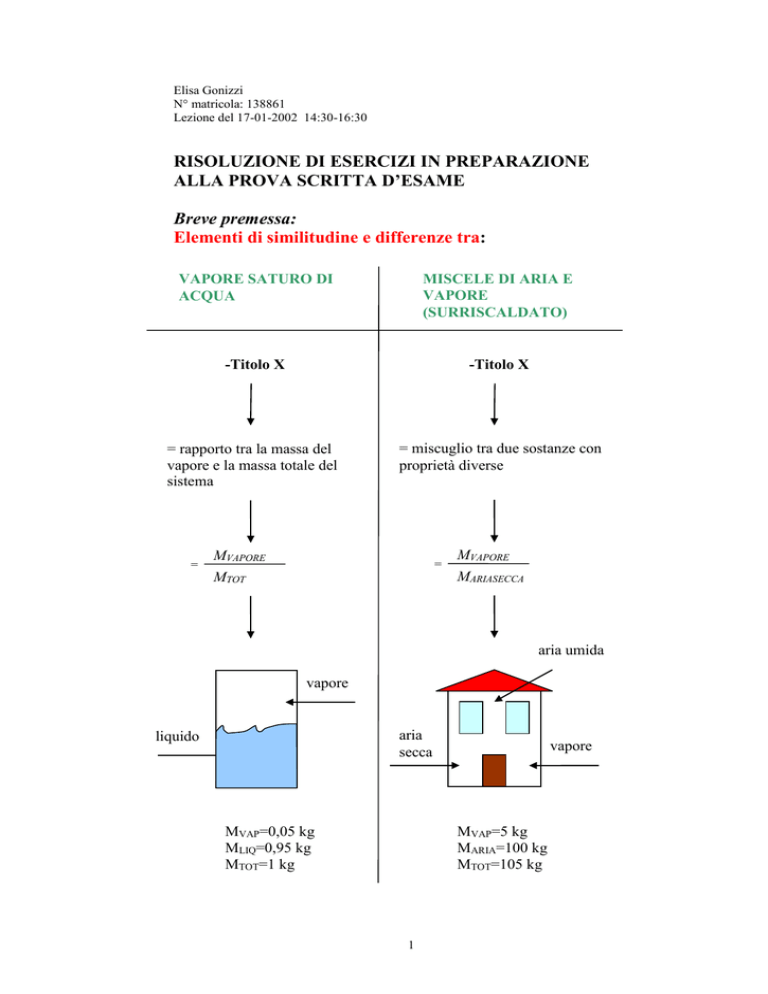
VAPORE SATURO DI
ACQUA
MISCELE DI ARIA E
VAPORE
(SURRISCALDATO)
-Titolo X
-Titolo X
= rapporto tra la massa del
vapore e la massa totale del
sistema
= miscuglio tra due sostanze con
proprietà diverse
=
MVAPORE
MTOT
=
MVAPORE
MARIASECCA
aria umida
vapore
aria
secca
liquido
MVAP=0,05 kg
MLIQ=0,95 kg
MTOT=1 kg
vapore
MVAP=5 kg
MARIA=100 kg
MTOT=105 kg
1
Lezione del 17-01-2002 14:30-16:30
x
kgV
0,05
 0,05
1
kgTOT
x
kg
5
 0,05 V
100
kg A
Si annulla
Due esercizi del compito in data 1-02-2001:
1° esercizio – Termodinamica (tolleranza +/- 5% (problema facile
perché di piccola tolleranza, cioè si dovranno risolvere calcoli derivanti da poche
formule))
pa
Z2
Z1
Aria
0
Q=1kcal
2
Lezione del 17-01-2002 14:30-16:30
Aria secca è contenuta entro uno stantuffo (quindi non c’è vapore), su cui grava
la pressione atmosferica ed un peso avente massa M pari a 100+AB kg che mantiene
costante la pressione al suo interno. L’area dello stantuffo A è pari a 100+CD cm 2 .
La temperatura iniziale T 1 del fluido entro lo stantuffo è pari a 20+EF °C. L’altezza
iniziale dello stantuffo, z 1 , è pari a 100mm. Al fluido viene comunicata dall’esterno
una quantità di calore Q pari ad 1 kcal. Il fluido si espande, sollevando il peso.
Trovare:
(1) - Temperatura finale T 2 ;
(2) - Altezza finale dello stantuffo z 2 .
Nota: Inserire i dati in base al proprio numero di matricola.
Esempio di svolgimento dell’esercizio prendendo in considerazione il
numero di matricola 123456 (ABCDEF)
Dati:
-
M=100+AB= 100+12=112 kg;
A=100+CD= 100+34=134 cm 2 ;
T 1 =20+EF= 20+56=76 C ;
z 1 = 100 mm;
Q=1 kcal (=4187 J).
La prima importante osservazione iniziale è che la trasformazione avviene a
pressione costante, è utile quindi cominciare l’esercizio disegnando un grafico
pertinente:
p
1u
L
1
2
3
v
Lezione del 17-01-2002 14:30-16:30
Iniziamo con calcolare il valore della pressione totale che rimarrà quindi costante
durante tutta la trasformazione:
(accelerazione di gravità
2
pari a 9,81 m/s )
p
tot = p
A+
M g
112kg  9,81m / s 2
= 101.325Pa 
 183.319 Pa
134  10 4 m 2
A
(pressione atmosferica
con valore fisso di 101.325 Pa)
Dall’equazione sui gas perfetti noi sappiamo che
p1V1  M A  R  T1
elementarmente si calcola il volume V1 facendo il prodotto tra la base dello stantuffo
e la sua altezza iniziale:
V1  A  z1  0,0134m 2  0,1m  0,00134m 3
e quindi si può ricavare M A 
p1  V
R  T1

183319 Pa  0,00134m 3
 0,002455kg
287  76  273
(La temperatura è stata trasformata in gradi Kelvin)
Sapendo inoltre che la quantità di calore Q è
M A  C p T2  T1   Q , dove C p è il calore specifico a pressione costante (pari a
1000),
allora T2  T1 
Q
4187 J
 1626,37C
 76C 
0,002455kg 1000
M A C p
4
Lezione del 17-01-2002 14:30-16:30
1626,37 C risulta essere la temperatura finale T2 , risposta al primo requisito del
problema.
Ora per trovare l’altezza finale dello stantuffo z 2 e rispondere perciò alla seconda
domanda del problema bisogna sempre rifarsi all’equazione dei gas perfetti,
prendendo questa volta in considerazione V 2 e la temperatura finale T2 , ricordando
che la pressione è comunque costante:
p 2 V2  M A  R  T2
da questa equazione si ricava poi
M  R  T2 0,002455kg  287  273  1626,37C 
V2  A

 0,0073002m 3
p
183319Pa
e ricordando di nuovo che un volume si calcola moltiplicando un’area per la sua
altezza si può facilmente trovare l’altezza finale dello stantuffo:
z2 
V2 0,0073002m 3

 0,544m
A
0,0314m
L’esercizio sarebbe adesso completato ma dato che la tipologia di problema
prevista per l’anno accademico 2001-2002 è in parte cambiata si propongono
due ulteriori requisiti in aggiunta ai precedenti, in tal modo l’esercizio sarà
veramente utile per la preparazione del nuovo esame
(3) - Calcolare il lavoro netto L’ sollevando il grave;
(4) - Valutare la variazione di entropia.
Si inizia rispondendo alla prima delle due ultime domande, si calcola quindi il lavoro
applicando la seguente formula:
L'  M  g  z  112kg  9,81 m s 2  0,444m  488J
dove g è l’accelerazione di gravità e z è la variazione dell’altezza dello stantuffo.
Lezione del 17-01-2002 14:30-16:30
Si può verificare l’esattezza del risultato sapendo che il lavoro L' è calcolabile anche
nel seguente modo:
5
Lezione del 17-01-2002 14:30-16:30


L'  V2  V1    p tot  p A   0,0073002m 3  0,00134m 3  183319 Pa  101325Pa   488 J
Si procede col rispondere alla seconda domanda:
In precedenza si era già definita la quantità di calore Q; ora tale valore lo si calcolerà
in infinitesimi:
dQ  M  C p  dT
C p è il calore specifico dell’aria.
Ora si può calcolare la variazione di entropia e rispondere alla quarta domanda:
2
S 2  S1  
1
2
T
dQ 2
dQ
dQ
  M C p 
 M C p  
 M  C p  log 2 
T
T
T
T1
1
1
 0,002455kg 1000  log
273  1626,37C
 4,159 J k
273  76C
2° Esercizio – Termodinamica (tolleranza +/- 5%)
pa
Z2
Z1
H2O
0
Q=1kcal
6
Lezione del 17-01-2002 14:30-16:30
Risolvere nuovamente l’esercizio n. 1, ma sostituendo vapore di acqua saturo
all’aria secca. In questo caso non è assegnata la temperatura iniziale T1, ma è invece
assegnato il titolo x1, che vale 0,1+F/74.
Trovare:
(1) - Titolo finale;
(2) - Altezza finale dello stantuffo z2.
Esempio di svolgimento dell’esercizio prendendo sempre in
considerazione il numero di
matricola 123456 (ABCDEF)
Dati:
-
M=100+AB= 100+12=112 kg;
A=100+CD=100+34=134cm2;
z1=100mm;
Q=1kcal (=4187J);
x 1=0,1+F/74=0,181.
Come per l’esercizio precedente è utile iniziare disegnando un altro grafico
pertinente:
1u
1,8
1
2
v
In questo caso la trasformazione avviene sia a pressione che a temperatura costante
quindi è sia isobara che isoterma; i due valori sono perciò i seguenti:
p  183319Pa  TSAT  117C
Bisogna qui calcolare il salto di entalpia in funzione del vapore saturo e quindi:
7
Lezione del 17-01-2002 14:30-16:30
H 2  H1  Q  4187J
h x  h L  x 2 hd
Si ricava poi l’entalpia specifica
Dove h L è l’entalpia del liquido e h d (anche chiamato r) è il vapore latente di
vaporizzazione ed è una grandezza tabellata
La differenza di entalpia è perciò


 
M acqua  hL2  x 2  hd  hL1  x1  hd  4187 J
e quindi facendo le dovute semplificazioni e raccoglimenti risulta
M acqua  hd  x 2  x1   4187 J
Ricordando che V1 =0,00134 m 3
M acqua 
V1
0,00134m 3

 0,00712kg
v 0,17839 m 3
kg
poiché v  v1  v d  0,001058  0,7093  0,1739
m3
kg

volume specifico
Il titolo x 2 è facilmente calcolabile e si può quindi rispondere al primo quesito:
x 2  x1 
Q
M acqua  R
 0,25 
4187 J
 0,502
0,007512  2211000
sapendo inoltre che
m3
v 2  v1  x 2 v d  0,001058  0,502  0,7093  0,3571
kg
e
V2  M acqua  v2  0,007512  0,3571  0,002683m3
allora si può trovare l’altezza dello stantuffo e rispondere perciò anche alla
seconda richiesta:
z2 
V2
 0,200m
V1
8
Lezione del 17-01-2002 14:30-16:30
L’esercizio sarebbe adesso completato ma dato che la tipologia di problema
prevista per l’anno accademico 2001-2002 è in parte cambiata si propongono
due ulteriori requisiti in aggiunta ai precedenti, in tal modo l’esercizio sarà
veramente utile per la preparazione del nuovo esame
(3) - Trovare il lavoro netto L;
(4) - Valutare la variazione di entropia.
Il lavoro netto si può calcolare applicando la stessa formula usata per l’esercizio
precedente, rispondendo così alla terza domanda:
L  M  g  z  L  112kg  9,81
m
 0,100m  109,87J
s2
Per trovare ora la variazione di entropia basta ricordare che essa è ricavabile dalla
seguente formula:
S  M acqua S d x 2  x1 
dove S d è l’entropia differenziale ed è calcolabile nel seguente modo:
Sd 
R
2211000
J
 Sd 
 5669
117  273
T
kg  K
(la temperatura è stata convertita in gradi Kelvin)
Sostituendo il valore trovato dell’entropia differenziale alla formula dell’entropia si
ottiene la risposta alla quarta domanda:
S  0,007512kg  5669
J
0,502  0,25  1073J/K
kg  K
9
Lezione del 17-01-2002 14:30-16:30
Un esercizio del compito in data 28-02-2001:
Esercizio di termodinamica (tolleranza +/- 15%)
MARIA
MACQUA
Entro un ambiente di volume V pari a 100+CD m3 si trova aria umida con
temperatura T1 pari a 20+E C ed umidità relativa  1 pari a 30+F%. Nell’ambiente
viene introdotta una massa di acqua M 2 , alla temperatura T1 , cosicché l’umidità
cresce ad un valore  2 pari a 60+F%. Ovviamente la temperatura cala, mancando
qualsiasi apporto di calore esterno. Determinare:
-
Massa di aria contenuta nell’ambiente;
Massa di acqua M2 da aggiungere.
Esempio di svolgimento dell’esercizio prendendo in considerazione
sempre il numero di matricola 123456 (ABCDEF)
Dati:
-
-
V=100+CD=134m3;
T1=20+E C =25 C ;
1=30+F%=36%;
2=60+F%=66%.
10
Lezione del 17-01-2002 14:30-16:30
Come utile osservazione iniziale è bene capire che la massa del volume dopo che è
stata introdotta l’acqua sarà la somma tra la massa del volume iniziale e la massa
dell’acqua introdotta, cioè
MV2=MV1+Macqua
Per calcolare la massa di aria contenuta nell’ambiente si ricorre all’equazione dei gas
perfetti nello stato fisico finale:
p A V  M A  R A  T1
p A V
R A  T1
e quindi M A 
Per la legge di Dalton , affermante che la somma delle pressioni parziali è uguale alla
pressione totale, la pressione dell’aria p A è uguale alla differenza tra la pressione
totale p TOT e la pressione parziale del vapore pV1 , cioè
p A  p TOT  pV1
Sapendo a sua volta che la formula del grado idrometrico  è

pV
 pV1   1  p SAT1  pV1  0,36  0,031709  0,01141BAR
p SAT

(pressione del vapore saturo, pari a 0,031709BAR)
allora p A  101325 1141  100184Pa
e quindi si può rispondere alla prima domanda definendo la massa dell’aria:
MA 
100184Pa 134m 3
 157kg
287  273  25
Il sistema è a energia costante e l’entalpia si è conservata quindi
2
H 2  H1  Q   vd  p
1
e quindi
11
Lezione del 17-01-2002 14:30-16:30
H2  M A  J 2
e
H 1  M A  J 1  M acqua  hL
eguagliando H 2 eH1 e facendo gli opportuni raccoglimenti si ottiene
M A J 2  J 1   M acqua  hL
J 2 e J 1 sono l’entalpia negli stadi finali ed iniziali mentre h L è l’entalpia del
liquido, esso si calcola nel seguente modo:
hL  C 2  t1  4,187  25  104,675
kJ
kg
C2 è il calore specifico dell’acqua.
L’entalpia specifica dell’aria umida J è data dalla formula
J  t  x2500  1,9  t 
Si può subito calcolare l’entalpia iniziale dopo aver trovato il titolo x1 in relazione
con il grado igrometrico  :
  p SAT1
0,36  0,031709
x1  0,622 
 0,622 
 0,007
pTOT    p SAT1
1,013  0,36  0,031709
quindi J 1  25  0,0072500  1,9  25  43,05
kJ
kg
Il valore della massa dell’acqua si può ricavare dalla seguente formula:
M acqua  M A   x 2  x1   0,597kg (risultato sbagliato!)
Ora però calcoliamo anche il valore dell’entalpia specifica nello stato finale:
J 2  J1 
M acqua
MA
 hL
J 2  t 2  x 2  2500  1,9  t 2 
12
Lezione del 17-01-2002 14:30-16:30
Proviamo inoltre a trovare la temperatura t2:
t2  1  x2  1,9  J 2  x2  2500
t2 
J 2  x 2  2500
 15,9C
1  1,9  x 2
Come per gli altri esercizi è utile disegnare un grafico pertinente:
x
0,66
2
0,36
2
19,5°C
1
22°C
25°C
T
La temperatura finale trovata ha un margine di errore molto elevato rispetto alla
temperatura presa come ipotesi all’inizio dell’esercizio quindi bisognerà calcolare
valori intermedi cosicchè il sistema non oscillerà. Dopo vari tentativi una esatta
approssimazione della temperatura risulta essere 19,55°C e quindi sostituendo tale
valore nelle formule precedenti si otterrà il giusto risultato della massa d’acqua, cioè
0,336kg.
13