ponzi127699

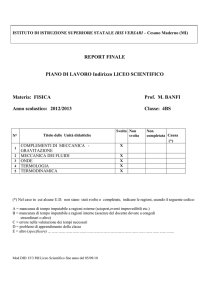
Alessandro Ponzi - matr. 127699 – Lezione 19/11/2001 – Ora 14.30 – 16.30
INTRODUZIONE : L’ACUSTICA
Lo studio di fenomeni acustici, dal punto di vista fisico, è strettamente legato ad altri
settori della scienza quali la fisiologia e la psicologia. La prima di queste studia il
meccanismo di percezione dei suoni e gli organi dell’udito l’altra studia le sensazioni
sonore in relazione agli stati d’animo prodotti in chi ascolta.
Già gli antichi filosofi greci (in particolare Aristotele) avevano osservato che quando
un corpo emette dei suoni si trova in uno stato di vibrazione, movimento che si
comunica all’aria circostante provocando onde paragonabili ai cerchi prodotti sulla
superficie di uno specchio d’acqua dalla caduta di un sasso. Si può dunque dire che
l’acustica studia i suoni e le onde sonore. Noi ci soffermeremo nello studio di queste
ultime, in particolare nella stesura dell’equazione di D’Alambert mostrando una sua
applicazione ed infine parleremo di Densità dell’energia sonora.
Nota storica : Jean Le Rond D’Alambert
Matematico e filosofo francese vissuto a Parigi tra il 1717 ed il 1783, membro
Dell’Academia a soli 20 anni scrisse varie opere ed esegui vari studi tra i quali il
moto delle corde vibranti dando una formulazione rigorosa del problema matematico
di queste :
“Il moto di una corda che vibra è descritto da un equazione differenziale alle
derivate parziali del 2º
ordine nelle variabili spazio e tempo, detta equazione di D’Alambert”
L’equazione di D’Alambert
Iniziamo col posizionare un volumetto di fluido (studieremo onde che si propagano
dell’aria) in un sistema di riferimento cartesiano tridimensionale :
dz
z
x
y
dy
dx
Figura 1
Le dimensioni del volumetto, scomposte nelle rispettive direzioni, danno il volume di
questo :
dV  dx  dy  dz
Conoscendo la relazione che lega la massa di un corpo con il suo volume
(massa=densita·volume) otteniamo, appunto, la massa del volumetto di fluido,
infatti :
-1-
Lezione 19/11/2001 – Ora 14.30 – 16.30
dM    dV    dx  dy  dz
(dove con  indichiamo la densità del fluido)
Ricaveremo l’equazione di D’Alambert dalla Legge di Newton :
F  ma
(forza=massa · accelerazione)
quindi mancano le forze in gioco e l’accelerazione, ricaviamo queste grandezze
partendo dall’accelerazione.
In una dimensione :
a
du
dt
portando tale relazione in un sistema di riferimento tridimensionale si avrà che :
a
dux duy duz


dt
dt
dt
(dove con ux,uy,uz indichiamo le velocità, delle particelle di fluido, riferite alle
rispettive direzioni figuranti a pedice)
Abbiamo cosi ottenuto la relazione :
du
 du
du 
dF  dM  x  y  z 
dt
dt 
 dt
[ Mettiamo in risalto il fatto che nell’equazione dell’accelerazione la velocità sarebbe
U detta velocità d’assieme totale
del sistema. Questa ha una componente detta
velocità acustica, (scomposta nelle componenti direzionali), da noi utilizzata ed un
componente, termine di trasporto, ritenuta da noi nulla in quanto facciamo l’ipotesi
che il fluido sia fermo, quindi a velocità nulla.]
Ci serve ora una espressione per la forza dF.
Sapendo che una forza può essere definita come una pressione esercitata su di una
superficie possiamo scrivere :
F  p A
(dove p è la pressione esercitata sulla superficie A)
Ora pensando ad una faccia del volumetto , preso ad esempio nella direzione x, e
bilanciando le forze in gioco si ha :
-2-
Lezione 19/11/2001 – Ora 14.30 – 16.30
x
Px
x+dx
Px+dx
A
x
Figura 2
La forza complessiva diviene :
dF x  ( Px  Px  dx )  dA  ( Px  Px  dx )  dy  dz
sfruttando il Teorema del Differenziale :
Px  dx  Px 
dP
 dx
dx
si ha :
Fx  
dP
 dV
dx
e ragionando lungo le tre direzioni :
 dP ˆ dP ˆ dP ˆ 
dF  
i 
 j
k  dV
dy
dz 
 dx
Eguagliando l’equazione con la Legge di Newton
du
 du
du 
dF    dV   x  y  z 
dt
dt 
 dt
si ottiene :
 dux duy duz 
 dP ˆ dP ˆ dP ˆ 


i


j

k

dV



dV

 dt  dt  dt 
 dx
dy
dz 



Infine, introducendo il gradiente della pressione, semplificando i termini comuni
(dV) avremo :
1ª equazione 
 P   
dU
dt
Arrivati a questo punto, ricordando che il volumetto è composto da un fluido, di
questo fluido ci interessa come la sua densità  vari al variare della pressione.
-3-
Lezione 19/11/2001 – Ora 14.30 – 16.30
Pensando ad un gas perfetto (il nostro caso il fluido) introdotto in un pistone
sottoposto, quindi, ad una pressione
P  P0  P 
P0+P’
p
P0
Gas
V0
v
Figura 3
Si nota che applicando una pressione P’ al gas il sistema oscilla attorno al punto di
equilibrio (p,v), lungo la tg a questo. Possiamo cosi ricavare la relazione tra pressione
e densità :

P  P0 V0   
e la pendenza della retta tangente è :
dP
d
essendo P0 = cost questo implica dP0 = 0 quindi d = d’.
Trascurando i termini di 2º ordine e semplificando i termini reciproci
( V0
 1
0
 1
) si ottiene :
dP  P0  V0    d

dP
 P0  V0  
d
introducendo l’equazione di stato dei gas perfetti :
P0  V0  R  T
abbiamo :
dP
 RT  c ²
d
2ª equazione 
-4-
Lezione 19/11/2001 – Ora 14.30 – 16.30
essendo c la velocità del suono ( c 
RT )
Questo risultato ci dice che il gas è tanto meno comprimibile quanto più la
propagazione avvine velocemente.
Abbiamo cosi due equazioni :
 P   
1.
2.
dU
dt
dP
 RT  c ²
d
in tre incognite P,u,.
L’equazione delle onde acustiche è legata a queste due.
È essenziale introdurre il Potenziale di velocità  :
  u
Risolvendo le equazioni precedenti utilizzando il Potenziale di velocità :
 P   0 
Perché queste siano uguali deve essere:
 P  0
d
dt
d
.
dt
d
   0  div( u)
dt
sostituendo si ha:
d
   0   ²
dt
Moltiplicando questa per c ² 
dP
d
ed inserendo  P   0
otteniamo un
dt
d
equazione differenziale di 2º grado detta equazione di D’Alambert :
d ²
 c ² ² 
dt
Questa equazione può essere risolta attraverso una :
-5-
Lezione 19/11/2001 – Ora 14.30 – 16.30
 Soluzione analitica (casi risolubili come onde piane progressive, onde piane
stazionarie, onde sferiche).
 Soluzione numerica (utilizzando metodi discreti tipo il metodo degli elementi
finiti o quello delle differenze finite dove si discretizza rispettivamente lo
spazio ed il tempo).
Si può concludere dicendo che :
”Risolvere l’equazione delle onde significa risolvere un
campo scalare del Potenziale della velocità”
Applicazione : intensimetro
L’intensimetro è uno strumento acustico che ricava l’intensità sonora ,o meglio la
velocità sonora utilizzata per calcolare l’intensità, tramite la pressione esercitata dal
suono cioè dalle particelle portatrici del suono, su microfoni (nel nostro caso due)
posizionati in un certo modo.
Noi useremo una coppia di microfoni che , ovviamente, devono essere uguali il più
possibile tra loro per avere un appropriato studio della variazione di pressione.
P1
P2
d
Figura 4
A livello circuitale si collegano le uscite dei microfoni ad un operazionale avente , a
sua volta, l’uscita collegata ad un integratore che presenterà, in uscita, un segnale
proporzionale alla componente cartesiana associata alla posizione dei microfoni,
della velocità. Per avere le tre componenti di uno spazio tridimensionale avremo
bisogno di tre coppie di microfoni posizionati lungo i tre assi cartesiani dello spazio
3D.
-6-
Lezione 19/11/2001 – Ora 14.30 – 16.30
+
P1
Integratore
Integratore
_
P2
Ux
Operatore
Figura 5
Ricaviamo l’intensità del suono lungo l’asse x .
I x  ux  P
Dove P 
P1  P2
.
2
Quello che ci manca è la ux ,qui entra in gioco l’intensimetro.
Utilizziamo l’equazione di Eulero
 P   0
du
dt
approssimando il metodo discreto delle differenze finite ed integrando otteniamo :
ux 
0
d
 (P
1
 P2 )dt
Supponendo il segnale sinusoidale si ha :
 Pdt  P  sen wtdt  P
max
max
1
sen wt
jw
cioè l’integratore non è altro che un filtro che divide per  (pulsazione), sfasando il
segnale di 90º e scende di 6dB per ottava.
È ora utile l’equazione di D’Alambertt per onde piane progressive.
In un onda piana progressiva tutte le particelle di un piano si muovono in un’unica
direzione con uguale velocità e pressione, una sorgente di questo moto può essere un
pistone che , in modo armonico, si muove all’interno di un tubo.
Figura 6
-7-
Lezione 19/11/2001 – Ora 14.30 – 16.30
Le condizioni al contorno sono date dall’ipotesi che all’istante t=0 lo spostamento sia
nullo (s=0) e la velocità sia massima (u=umax).
L’equazione di D’Alambert per un onda piana progressiva è :
   max  cos( wt  kx )
dove k=w/c è il numero d’onda.
Utilizzando la notazione di Eulero, la rappresentazione della precedente formula si
può scrivere :
  max  e j ( wt kx ) 
in quanto solo la parte reale della formula è coerente in un contesto fisico. Spesso
comunque Re viene omesso.
Nel nostro caso, essendo in una dimensione, si ha :
u   
d
dx
quindi
u   jkmax  e j ( wt kx )
Imponendo le condizioni al contorno si ha:
u  umax  e j ( wt kx )

u( x, t )  umax  e j ( wt kx )
E la Pressione ?
Sappiamo che :
P   0
d
dt
allora possiamo scrivere
P   j   0    max  e j ( wt kx )
perciò :
P ( x , t )   0  c  u( x , t )
e volendo calcolare l’intensità relativa :
-8-
Lezione 19/11/2001 – Ora 14.30 – 16.30
i  P  u  0  c  umax ²  e 2 j ( wt kx )
Infine facendo una media temporale dell’intensità istantanea si ricava il valore di
intensità acustica detta anche intensità media :
1T
1
V 
I   i ( t )dt   0  c  umax ²  
T0
2
 m² 
Densità dell’energia sonora
La propagazione di un’onda, in un mezzo qualsiasi, e precisamente la variazione di
velocità e pressione a livello locale, comporta anche la propagazione di energia.
Per misurare tale energia si introduce il coefficiente di densità di energia che dà una
misura dell’energia per unità di volume :
D
E J 
V  m ³ 
Se torniamo a pensare ad un pistone in un cilindro, detta A l’area del pistone avremo
che :
V  A c  t
E  A I  t
Prendendo t=1 secondo e sostituendo tali grandezze nella definizione di densità di
energia ricaviamo che :
D
I
c
Potendo scrivere l’intensità dal punto di vista energetico come un contributo
potenziale ed un contributo cinetico :
I
1
E pot  Ecin   1  PRMS ²   0  c  uRMS ²
2
2  0  c

possiamo ricavare l’equazione di densità di energia con i contributi energetici :
D

1  PRMS ²
  0  uRMS ² 

2  0  c²

-9-
Lezione 19/11/2001 – Ora 14.30 – 16.30
Si può cosi affermare che :
“La densità dell’energia sonora è per definizione costante”.
Certo le sue componenti potenziale e cinetica si travasano tra loro, compensando le
proprie variazioni.
Notiamo che nel caso di un onda piana progressiva
c
I
D
U
I
D
e nel caso generale
dove U è diverso da c, cioè si può dire che :
”la velocità dell’energia è minore o uguale della velocità del suono”
dove l’uguaglianza vale solo nel caso di onde piane progressive.
Da quanto detto, per conoscere le caratteristiche del sistema da analizzare, in acustica
si ha che :
 dal punto di vista fisico è necessario rilevare i valori di velocità e di pressione.
 dal punto di vista energetico è necessario rilevare i valori di intensità sonora e di
densità di energia.
Introduciamo per finire il livello di densità.
Ogni grandezza acustica è misurata in dB. Introduciamo alcuni livelli :
PRMS ²
Prif  2  105 Pa
Prif ²
v ²
P
 livello di velocità Lv  10 log RMS
v0  0  5  108 m / s
v0 ²
0  c
I
 livello di intensità LI  10 log
I 0  1  1012W / m ²
I0
I
D
 livello di densità LD  10 log
D0  0  2.94  1015 J / m ³
D0
c
 livello di pressione L p  10 log
Per un onda piana progressiva tutti questi livelli sono uguali tra loro, in generale il
livello di intensità è più piccolo o al più uguale a quello di densità :
LI  LD
-10-
Lezione 19/11/2001 – Ora 14.30 – 16.30
il livello di pressione può superare il livello di densità al più di 3 dB tanto come
quello di velocità.
Si definisce indice di reattività del nostro corpo la differenza che vi è tra il livello di
densità e quello di intensità :
LD  LI
quanto più è reattivo il nostro corpo tanto più questo indice è grande.
Spesso si indica l’indice di reattività come la differenza tra il livello di pressione e
quello di intensità :
LP  LI
ma questo è sbagliato in quanto questa differenza potrebbe essere negativa , un indice
negativo indicherebbe che un campo si può propagare più velocemente di un onda
piana progressiva, per quanto detto prima questo è impossibile.
-11-
Lezione 19/11/2001 – Ora 14.30 – 16.30
Appendice
Vibrazione : movimento oscillatoria di particelle attorno alla posizione di equilibrio.
Onde : si osserva spesso che le perturbazioni di una data grandezza fisica, in una
certa regione dello spazio, si trasmette alle regioni circostanti. Questo
comportamento, comune a molti fenomeni fisici, è noto come propagazione delle
onde. La propagazione del suono, della luce, delle vibrazioni di un corpo elastico
sono esempi di questo comportamento.
Accelerazione : variazione di velocità che un copro subisce in un certo intervallo di
tempo.
Legge di Newton : ogni corpo mantiene il suo stato di quiete o di moto rettilineo
uniforme finché forze esterne, agendo su di esso, non lo costringono a mutare il suo
stato. La forza, quindi, può essere espressa come la massa del corpo moltiplicata per
l’accelerazione che subisce tale corpo.
Equazione di stato dei gas perfetti : dette p la pressione, v il volume specifico, T la
temperatura espressa in Kelvin, R0 costante universale (=8314 J/mol K) , la massa
molare degli elementi componenti il gas si ha :
p  v    R0  T
Potenziale : grandezza scalare tridimensionale tale che il suo gradiente è uguale ad
un vettore dato,nel nostro caso la velocita.
-12-