Inferenza statistica

Inferenza statistica nel modello lineare : regressione semplice
Volendo costruire un modello che spieghi il Peso (espresso in kg) in funzione dell’Altezza (espressa in cm) si è
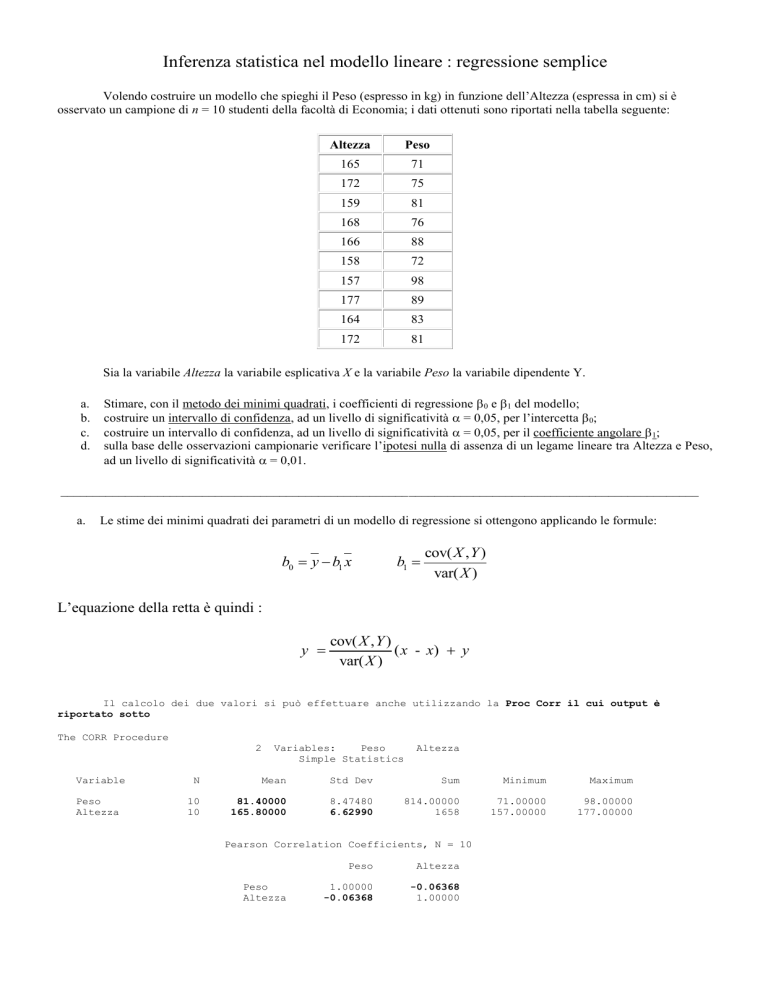
osservato un campione di n = 10 studenti della facoltà di Economia; i dati ottenuti sono riportati nella tabella seguente:
Altezza
Peso
165
71
172
75
159
81
168
76
166
88
158
72
157
98
177
89
164
83
172
81
Sia la variabile Altezza la variabile esplicativa X e la variabile Peso la variabile dipendente Y.
a.
b.
c.
d.
Stimare, con il metodo dei minimi quadrati, i coefficienti di regressione 0 e 1 del modello;
costruire un intervallo di confidenza, ad un livello di significatività  = 0,05, per l’intercetta 0;
costruire un intervallo di confidenza, ad un livello di significatività  = 0,05, per il coefficiente angolare 1;
sulla base delle osservazioni campionarie verificare l’ipotesi nulla di assenza di un legame lineare tra Altezza e Peso,
ad un livello di significatività  = 0,01.
___________________________________________________________________________________________________
a.
Le stime dei minimi quadrati dei parametri di un modello di regressione si ottengono applicando le formule:
b0  y  b1 x
b1 
cov( X , Y )
var( X )
L’equazione della retta è quindi :
y 
cov( X , Y )
( x - x)  y
var( X )
Il calcolo dei due valori si può effettuare anche utilizzando la Proc Corr il cui output è
riportato sotto
The CORR Procedure
2
Variable
Peso
Altezza
Variables:
Peso
Simple Statistics
Altezza
N
Mean
Std Dev
Sum
Minimum
Maximum
10
10
81.40000
165.80000
8.47480
6.62990
814.00000
1658
71.00000
157.00000
98.00000
177.00000
Pearson Correlation Coefficients, N = 10
Peso
Altezza
Peso
Altezza
1.00000
-0.06368
-0.06368
1.00000
Un modo per effettaure i calcoli necessari senza utilizzare SAS sono contenuti nel seguente schema:
Totale
xi
yi
xi2
yi2
xi yi
165
71
27.225
5.041
11.715
172
75
29.584
5.625
12.900
159
81
25.281
6.561
12.879
168
76
28.224
5.776
12.768
166
88
27.556
7.744
14.608
158
72
24.964
5.184
11.376
157
98
24.649
9.604
15.386
177
89
31.329
7.921
15.753
164
83
26.896
6.889
13.612
172
81
29.584
6.561
13.932
1.658
814
275.292
66.906
134.929
Le formule da utilizzare sono le seguenti :
1 n

cov( X , Y )    xi yi   x y
n  i 1

n
2
1

var( X )    xi2   x
n  i 1 

L’equazione della retta di regressione è quindi:
Y  94.9 – 0.081 X
Per la determinazione degli intervalli di confidenza i calcoli sono contenuti nello schema seguente:

yi  y i

2
xi
yi
y i  94.9 – 0.081 xi
165
71
81,46512
109,5187
172
75
80,89535
34,75516
159
81
81,95349
0,909136
168
76
81,22093
27,25812
166
88
81,38372
43,77515
158
72
82,03488
100,6988
157
98
82,11628
252,2927
177
89
80,48838
72,44774
164
83
81,54651
2,11263
172
81
80,89535
0,010951
814
814
643,779
Totale 1.658
L’errore standard della regressione, dato dalla radice quadrata della varianza residua, è:
S
b.
1 n
1
2
 yi  yi    643, 779  8,97064

n  2 i 1
8
L’intervallo di confidenza per 0 è:


  0  t ,n2 * SE ( 0 );  0  t ,n2 * SE ( 0 )  =

2
2

=
c.
94.9  2.36*74.83,94.9  2.36*74.83  77.67, 267.46
L’intervallo di confidenza per 1 è:


  1  t ,n2 * SE (  1 );  1  t ,n2 * SE (  1 )  =

2
2

=
0.081395  2,36*0.451, 0.081395  2,36*0.451  1.12144,0.9587
Si osservi che per  = 0,05 e n – 2 = 8 gradi di libertà è:
t
2
d.
 t0.025,8  2.36
,n 2
Dove si trovano questi valori nell’output SAS?
The REG Procedure
Dependent Variable: Peso
Number of Observations Read
10
Analysis of Variance
DF
Sum of
Squares
Mean
Square
1
8
9
2.62093
643.77907
646.40000
2.62093
80.47238
Root MSE
Dependent Mean
Coeff Var
8.97064
81.40000
11.02044
Source
Model
Error
Corrected Total
R-Square
Adj R-Sq
F Value
Pr > F
0.03
0.8613
0.0041
-0.1204
Parameter Estimates
Variable
DF
Parameter
Estimate
Intercept
Altezza
1
1
94.89535
-0.08140
Standard
Error
74.83282
0.45102
t Value
Pr > |t|
1.27
-0.18
0.2404
0.8613
SE ( 1 )
0
SE (  0 )
1
SE ( 1 )
e.
L’ipotesi da verificare è:
 H 0 : 1  0

 H1 : 1  0
A tal fine si può utilizzare la statistica test:
T
1
SE ( B1 )
Se l’ipotesi nulla è vera, T si distribuisce, al variare del campione come una variabile casuale t di Student con n – 2 gradi di
libertà.
Il valore empirico della statistica – test è:
T
0.81395
 0.1805
0.451
Per n – 2 = 8 gradi di libertà e per /2 = 0,005 è:
t0.005,8  3.355
Essendo t  t
2
,n2
si rifiuta l’ipotesi di assenza di dipendenza lineare della variabile Peso (Y) dalla variabile Altezza (X), ad
un livello di significatività  = 0,01.