Area di un grafico

Area di un grafico
L’integrale definito

b
a

b
a
f ( x)dx rappresenta l’area sottesa dal grafico di f(x) e si calcola
f ( x)dx  F (b)  F (a) dove F(x) rappresenta la primitiva.
Questo quando la funzione f(x) è sempre positiva o nulla.
2
p.e.

2
1
x3
2
13
86
1 3 2 2 4
( x  1)dx   x  (  2)  (  1)  (
)(
)  
3
3
3
3
3
3 3 3
1
3
2
Se f(x)<0 allora Area 

b
a
1
b
f ( x)dx  F (b)  F (a)    f ( x)dx  ( F (b)  F (a))
a
x3
1
03
1 3
2
)  0   allora l’area è data da 2/3
p.e.  ( x  1)dx   x  (  1)  (  0)  (
0
3
3
3
3
3
0
1
3
2
Quando una funzione è sia positiva che negativa in un intervallo, allora spezzo l’integrale in
intervalli di valori positivi e negativi mettendo il meno davanti a quest’ultimi.
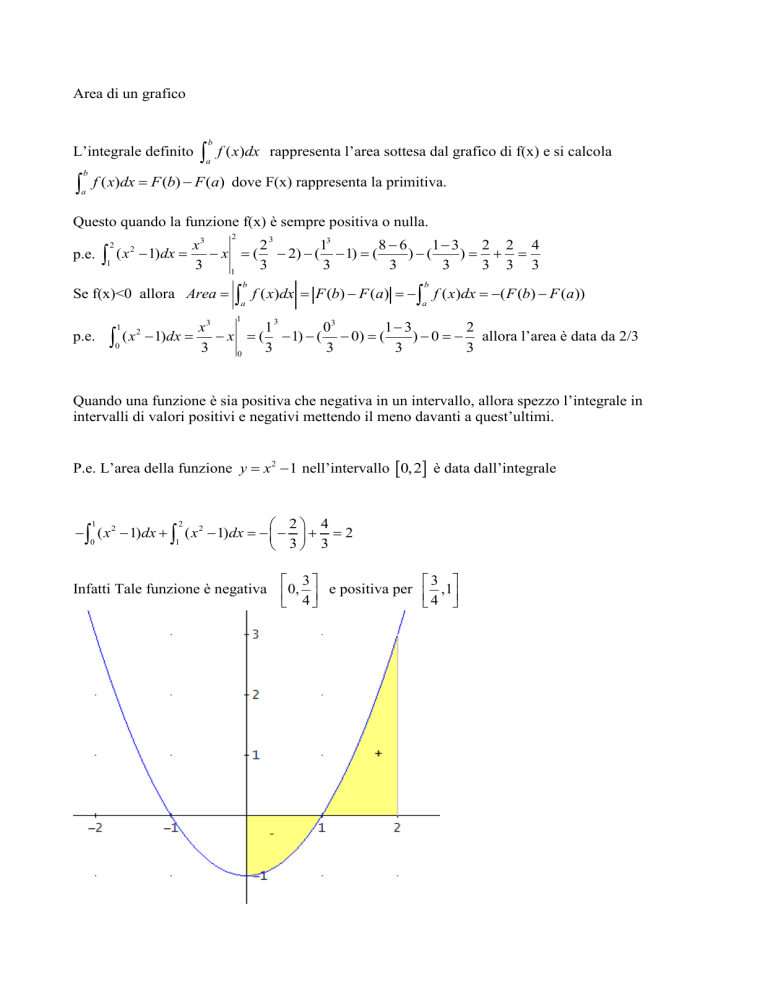
P.e. L’area della funzione y  x 2  1 nell’intervallo 0, 2 è data dall’integrale
1
2
 2 4
  ( x 2  1)dx   ( x 2  1)dx        2
0
1
 3 3
 3
3 
Infatti Tale funzione è negativa  0,  e positiva per  ,1
 4
4 
Area compresa tra due funzioni
Date le funzioni y=f(x) e y=g(x) con g ( x)  f ( x) l’area compresa tra le due funzioni in un
intervallo  a, b è data da
b
b
b
a
a
a
Area   f ( x)dx   g ( x)dx   ( f ( x)  g ( x))dx
Area tra tre o più funzioni
L’area di tre funzioni y  f ( x) y  g ( x) y  h( x) che si intersecano nei punti a,b, c
f h  a
f g b
g h  c
b
c
a
a
b
c
È data da Area   f ( x)dx   g ( x)dx   h( x)dx
Il verso di percorrenza è orario e l’ultimo indice superiore coincide con il primo indice inferiore
a=a.
Integrali impropri
In cui un estremo, o entrambi gli estremi, non sono punti in cui la funzione è continua.
Se p.e. dato l’intervallo  a, b , la funzione non è continua in b allora si sceglie un punto 
Interno all’intervallo e si prende per integrale:

lim  f ( x)dx  lim( F ( )  F (a))
 b a
 b
analogamente per a
a
lim  f ( x)dx  lim( F (b)  F ( ))
 a 
 a
È possibile che tale estremo sia infinito allora
lim

b
b  a
p.e.



f ( x)dx  lim ( F (b)  F (a)) oppure
b 
lim

b
a  a
f ( x)dx  lim ( F (b)  F (a))
a 

1
1

b
dx  2
dx  lim 2arc tan x 0  lim (2arc tan b  ar c tan 0)  lim 2ar tan b  2  
2
0
b 
b 
b 
x 1
x 1
2
2
Volume di solidi generati da curve in rotazione attorno agli assi.
Se considero un grafico y  f ( x) nell’intervallo  a, b con f ( x)  0 e lo faccio ruotare attorno
all’asse x , ottengo una superfice, dove le sezioni perpedicolari a x sono tante circonferenze.
Per calcolare il Volume di tale superficie considero l’intevallo,  x, x  x e calcolo il volume di
Tale sezione che sarà  f 2 ( x)x , sommando tutte queste sezioni tra a e b ottengo il volume:
b
Volume    f 2 ( x)dx
a
P.e. se ho una retta y=x facendo ruotare la parte nell’intervallo
3
cono Volume    x 2 dx 
0
0,3 ,ottengo il volume del
3
x3
27

 9
30
3
Se la funzione ruota attono all’asse y considero la funzione in funzione di y x  g ( y )
b
E Volume    g 2 ( y)dy
a