LA DIPENDENZA STATISTICA
LA TEORIA DELLA CORRELAZIONE
In una indagine statistica si cerca spesso di scoprire se fra due variabili
statistiche esiste o meno un legame e, ammesso che esista, si vuole sapere
qual è l’intensità di questo legame.
Il primo passo utile per indagare qualitativamente il legame fra due variabili x
e y, consiste nel disegnare il diagramma di dispersione.
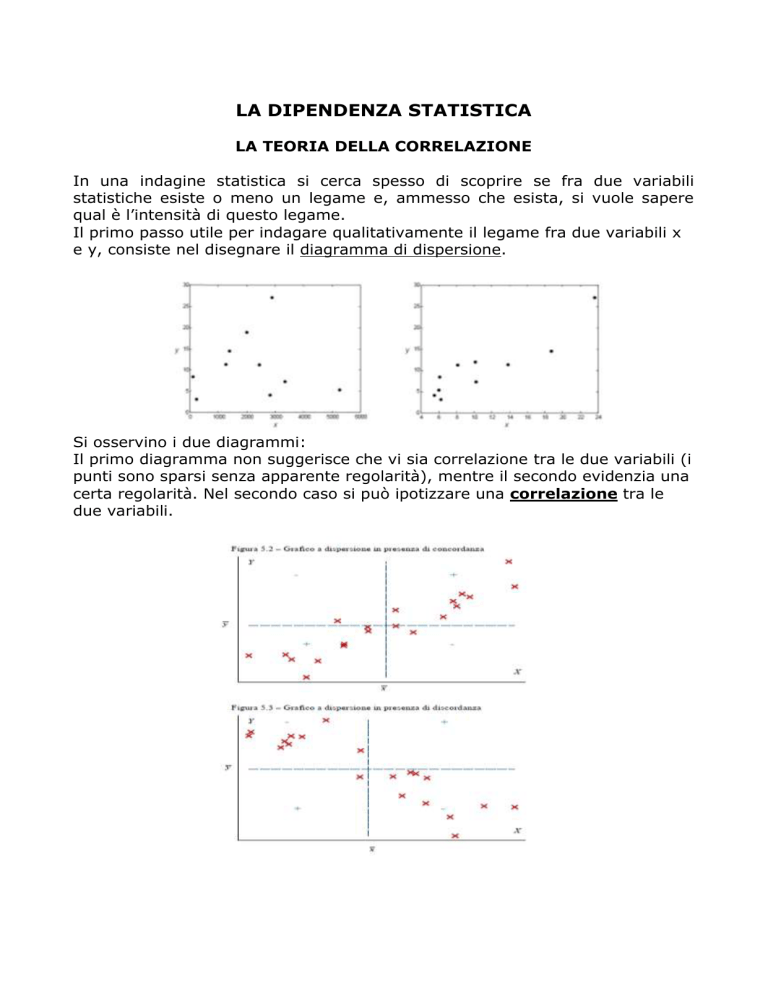
Si osservino i due diagrammi:
Il primo diagramma non suggerisce che vi sia correlazione tra le due variabili (i
punti sono sparsi senza apparente regolarità), mentre il secondo evidenzia una
certa regolarità. Nel secondo caso si può ipotizzare una correlazione tra le
due variabili.
Covarianza
La covarianza consente di verificare se fra due variabili statistiche X e Y esiste
un legame lineare e, in caso affermativo, se vi è concordanza oppure
discordanza. Siano date le osservazioni
(x1,y1), (x2,y2), …, (xn,yn).
rilevate su n unità statistiche e si indichino con
le medie di X e Y rispettivamente. La covarianza è data da
Calcolo del coefficiente di correlazione
Il segno della covarianza, quando essa è diversa da zero, indica se vi è
concordanza o discordanza ma il suo valore dipende dall’unità di misura e
pertanto non dà informazioni sull’intensità del legame lineare.
Un indice in grado di fornire tale informazione è il coefficiente di correlazione.
Siano X e Y due variabili statistiche, il coefficiente di correlazione è dato da
ed è un indice dell’intensità del legame lineare.
Sostituendo l’espressione della covarianza e degli scarti quadratici medi nella
formula del coefficiente di correlazione si ottiene
Il
coefficiente
di
correlazione
assume
valori
nell’intervallo
Corr(X,Y)
(−1,1). Il coefficiente
di correlazione vale 1
in valore assoluto se
fra le variabili vi è
perfetta dipendenza
lineare .Quando vi è indipendenza tra le due variabili le osservazioni si
dispongono in modo casuale fra le quattro porzioni del grafico a dispersione e
pertanto non vi è né una prevalenza di prodotti degli scarti positivi né una
prevalenza di prodotti degli scarti negativi. In questo caso la covarianza è
nulla.
Infine la covarianza può essere nulla anche quando vi dipendenza fra le
variabili, ma la dipendenza è non lineare.












