Diapositiva 1

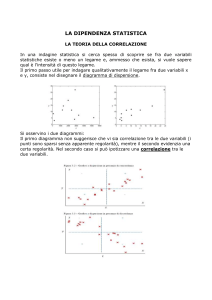
SIGNIFICATIVITÀ STATISTICA
DEL COEFFICIENTE DI CORRELAZIONE
Occorre però sempre verificare se la correlazione sia l’effettiva espressione di
un’associazione tra le variabili oppure sia frutto della variabilità casuale. Poiché anche il
coefficiente di correlazione, come altre statistiche, è soggetto alla fluttuazione di
campionamento, è necessario verificare l’ipotesi zero di nessuna correlazione delle due
variabili nella popolazione, H 0    0. Anche per il coefficiente r esistono delle tavole (Tabella
1) che, in rapporto ai gradi di libertà (che per la correlazione sono il numero di coppie meno
2), forniscono il valore critico al desiderato livello di significatività. In mancanza della tabella
dei valori critici, è previsto il ricorso alla distribuzione del t di Student, applicando il seguente
algoritmo:
t  r
n2
1 r2
che permette di definire per ogni valore di r il corrispondente livello di probabilità utilizzando
le tabelle del t sempre con n – 2 gradi di libertà.
La correlazione, r =+ 0.86, tra azoto ureico e pressione per 13 gradi di libertà (g.l. = 15 – 2)
supera il valore critico 0.6411 al livello  = 0.01 e permette il rifiuto dell’ipotesi nulla. A
identica conclusione si perviene con la trasformazione t: il valore ottenuto, r = 6.076, supera
il valore critico 3.012. Lo stesso vale per la correlazione tra colesterolo e creatinina (r = –
0.85); non deve trarre in inganno il segno negativo, che riguarda il tipo di correlazione, ma
che non influisce sulla significatività, unicamente dipendente dal grado di associazione.
Elementi di Statistica medica
Pasquale Bruno Lantieri, Domenico Risso, Giambattista Ravera
Copyright © 2007 – The McGraw-Hill Companies s.r.l.
Il coefficiente di correlazione ci fornisce ulteriori informazioni: il suo quadrato prende
il nome di coefficiente di determinazione, ed equivale alla proporzione di variabilità
congiunta. Nel nostro esempio di correlazione tra azoto ureico e pressione, r2 =
0.862 = 0.74 indica che il 74% della variazione pressoria è spiegata dall’azoto ureico
e viceversa, cioè esiste una variabilità comune del 74%, mentre il rimanente 26% di
variabilità è legato ad altri fattori che non si è in grado di spiegare con la sola
correlazione.
Di seguito si riportano alcuni ulteriori aspetti da sottolineare e da ricordare:
• se la relazione tra due variabili non è lineare, il coefficiente di correlazione non è
una misura appropriata della forza di relazione;
• il coefficiente di correlazione può essere pesantemente influenzato da osservazioni
particolarmente scostate dalle altre;
• a rigori, la correlazione stimata vale solo per gli intervalli di valori considerati nel
calcolo in quanto al di fuori del “range” dei valori sperimentali, la relazione potrebbe
essere diversa; l’estrapolazione non dovrebbe mai essere eseguita o quantomeno i
risultati dovrebbero essere valutati con estrema cautela.
Elementi di Statistica medica
Pasquale Bruno Lantieri, Domenico Risso, Giambattista Ravera
Copyright © 2007 – The McGraw-Hill Companies s.r.l.
Elementi di Statistica medica
Pasquale Bruno Lantieri, Domenico Risso, Giambattista Ravera
Copyright © 2007 – The McGraw-Hill Companies s.r.l.