Tema d'esame (come esercizio) n.3
1. Chiarire come sia possibile, note le elasticità e un punto di equilibrio di mercato,
ricostruire le curve di domanda e di offerta.
Le curve di domanda e di offerta, conoscendo l’elasticità e il punto di equilibrio di mercato,
possono essere ricostruite nel seguente modo. Per semplicità si vengono ipotizzate delle curve
di domanda e di offerta lineari.
Prima di procedere con la ricostruzione delle due curve è bene spiegare il concetto di elasticità.
Per elasticità si tratta della variazione percentuale di una variabile prodotta dall’incremento di un
punto percentuale di un’altra variabile.
Sapendo che le curve di domanda (Qd) e di offerta (Qo) lineare sono espresse nel seguente
modo: Qd= a-bP e Qo= c+dP
Inoltre l’elasticità rispetto al prezzo della domanda e dell’offerta può essere espressa come:
E = (P/Q)(AQ/AP)
AQ/AP nelle curve lineari è costante. Pertanto si può sostituire il valore marginale nella formula
dell’elasticità con d per l’offerta e con –b per la domanda. Di conseguenza le formule sono le
seguenti:
ED= -b(P*/Q*)
EO= d(P*/Q*)
P* e Q* sono rispettivamente il prezzo e la quantità di equilibrio per i quali disponiamo di dati e
ai quali vogliamo adattare le curve. Poiché abbiamo come termini noti EO, ED, P* e Q*
possiamo sostituirli nell’equazione e trovare le incognite –b e d.
I valori –b e d trovati li possiamo utilizzare per risolvere le equazione della curva di domanda e
di offerta sopra indicate trovando le incognite a e c.
bene
2. Qual è lo scopo della costruzione precedente? Considerare anche degli esempi.
Lo scopo della costruzione precedente è quello di analizzare e prevedere gli effetti delle
variazioni delle condizioni del mercato come ad esempio la fluttuazione di variabili come il PIL, i
costi di produzione. Ad esempio possiamo studiare il comportamento dei prezzi del rame,
analizzando quali potrebbero essere gli effetti nel caso vi fosse un calo della domanda pari ad
20%. Quindi spostiamo la curva di domanda del 20% verso sinistra, riducendo cosi la quantità
domandata ad un 80% del livello normale, per ogni valore di prezzo. Per tanto per calcolare la
nostra curva di domanda possiamo procedere come segue. Q= 0,8 (a-bP).
Si può quindi dedurre che l’offerta rimane invariata.
Infine eguagliando la quantità offerta e la quantità domandata si può ricavare il prezzo con una
riduzione del 20%.
Bene, veda anche l’esempio del petrolio cogliendo qual sia il contenuto di cambiamento in quel
caso
3. E' ragionevole utilizzare curve di domanda e offerta lineari? Con riferimento alla
domanda, considerare vantaggi e svantaggi, anche con riferimento alla misura
dell’elasticità.
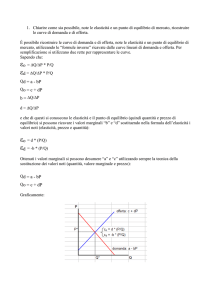
È ragionevole utilizzare curve di domanda e offerta lineari in quanto essendo delle rette
semplificano i calcoli ma rappresentano la realtà solamente approssimativamente. Questo è
possibile notarlo soprattutto per i casi estremi, infatti dal grafico sotto riportato si evince che ad
un prezzo pari a 0 la quantità domandata è 8 e viceversa ad un prezzo 4 la quantità domandata
è 0. Nella realtà non è cosi in quanto ad un prezzo zero la quantità domandata sarebbe infinita
ed ad un prezzo 4 è impossibile che non vi siano quantità domandate.
Bene, affronti anche l’aspetto della elasticità variabile su una retta di domanda: è un vantaggio o no per
l’uso di quella funzione?
Valutazione complessiva D