1. Chiarire come sia possibile, note le elasticità e un punto di equilibrio di mercato, ricostruire
le curve di domanda e di offerta.
È possibile ricostruire le curve di domanda e di offerta, note le elasticità e un punto di equilibrio di
mercato, utilizzando le “formule inverse” ricavate dalle curve lineari di domanda e offerta. Per
semplificazione si utilizzano due rette per rappresentare le curve.
Sapendo che:
εo = ∆Q/∆P * P/Q
εd = ∆Q/∆P * P/Q
Qd = a - bP
Qo = c + dP
b = ∆Q/∆P
d = ∆Q/∆P
e che di questi si conoscono le elasticità e il punto di equilibrio (quindi quantità e prezzo di
equilibrio) si possono ricavare i valori marginali “b” e “d” sostituendo nella formula dell’elasticità i
valori noti (elasticità, prezzo e quantità):
εo = d * (P/Q)
εd = -b * (P/Q)
Ottenuti i valori marginali si possono desumere “a” e “c” utilizzando sempre la tecnica della
sostituzione dei valori noti (quantità, valore marginale e prezzo):
Qd = a - bP
Qo = c + dP
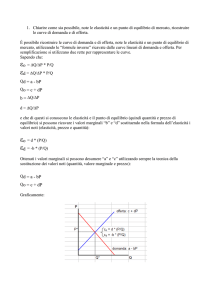
Graficamente:
2. Qual è lo scopo della costruzione precedente? Considerare anche degli esempi.
Lo scopo della costruzione precedente è quello di capire e prevedere gli effetti di cambiamenti sul
mercato. Questi cambiamenti potrebbero essere ad esempio il prezzo di un determinato bene e il
reddito percepito dal consumatore. La costruzione precedente può servire per studiare come un
aumento o una diminuzione del prezzo o del reddito influiscano sul mercato facendo spostare una o
entrambe le curve.
Consideriamo quanto detto con un esempio sulla domanda e offerta di lungo periodo nel mercato
del rame, prendendo in analisi l’incidenza del prezzo nel mercato.
Noti i seguenti dati:
Q = 12 milioni di tonnellate l’anno
P = 2 $/Kg
εo = 1,5
εd = -0,5
e tenendo presente le equazioni esposte al quesito n. 1, che per praticità ricordo di seguito:
εo = ∆Q/∆P * P/Q
εd = ∆Q/∆P * P/Q
Qd = a - bP
Qo = c + dP
b = ∆Q/∆P
d = ∆Q/∆P
si ricavano dapprima i valori marginali “b” e “d”:
εd = ∆Q/∆P * P/Q
- 0,5 = - b * (2/12)
b=3
εo = ∆Q/∆P * P/Q
1,5 = d * (2/12)
d=9
e in seguito i valori di “c” e “d”:
Qd = a - bP
12 = a – 3 * (2)
a = 18
Qo = c + dP
12 = c + 9 * (2)
c = -6
A questo punto si ottengono le due curve lineari:
Domanda:
Q = 18 – 3P
Offerta:
Q = -6 + 9P
Come accennato precedentemente oltre al prezzo è presente un’altra variabile che influisce sul
mercato: il reddito. Quindi considerando la curva di domanda anche in funzione del reddito questa
diventerebbe:
Q = a – bP + fRD
In cui RD è un indice del reddito aggregato pari a 1 e l’elasticità della domanda rispetto al reddito è
1,3.
Tenendo presente che:
εd = ∆Q/∆RD * RD/Q
si utilizza come ai punti precedenti la tecnica della sostituzione dei valori noti e si ottiene in primo
luogo f:
1,3 = f * (1/12)
f = 15,6
ed infine “a”:
12 = a – 3*(2) + 15,6*(1)
a = 2,4
Ottenendo così la curva di domanda.
Il reddito è un aspetto marginale; i due esempi importanti del capitolo sono quello in cui
modifichiamo la curva di domanda del rame e quello della curva di offerta del petrolio; si tratta di
riportarli come concetti, non come formule e valori numerici, il giorno dell’esame non avrebbe i
dati che ad esempio usato qui sopra.
3. E' ragionevole utilizzare curve di domanda e offerta lineari? Con riferimento alla domanda,
considerare vantaggi e svantaggi, anche con riferimento alla misura dell’elasticità.
Sì, è ragionevole utilizzare curve di domanda e offerta lineari in quanto è possibile eseguire calcoli
su quantità, prezzo ed elasticità in modo più comodo e semplice. Tuttavia, queste non rappresentano
in modo preciso la realtà, la rappresentano solo approssimativamente.
Per comprendere meglio come l’utilizzo di una retta per la curva di domanda non rappresenti del
tutto la realtà basta osservare il grafico sotto riportato.
Come si può notare,ad un prezzo uguale a zero, la quantità domandata è 8.
È evidente che in una situazione reale ciò è difficile che accada in quanto ad un prezzo zero, la
quantità domandata sarà sicuramente maggiore, ed è altrettanto impensabile che ad un prezzo 10
non vi siano quantità domandate.
Anche per quanto concerne l’elasticità non costante su una retta, è improbabile che nella realtà
questa risulti a zero in prossimità di un prezzo zero, e infinta al prezzo 10.
Questo accade perché applicando la formula dell’elasticità:
εd = ∆Q/∆P * P/Q qualora si divida per un prezzo zero l’elasticità sarà infinita, qualora si divida
per una quantità a zero si otterrà zero.
… ma il fatto che l’elasticità sia variabile, crescendo con i prezzi, può essere un punto di forza di
questo tipo di rappresentazione.
Così com’è ora, il compito riceverebbe la valutazione D, ma la risposta 2 non sarebbe fattibile
realisticamente.