capitalizzazione - Istituto Fermi Polo Montale

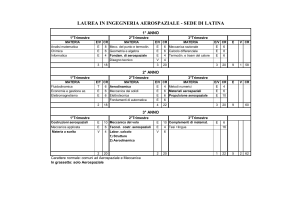
CAPITALIZZAZIONE SEMPLICE
M  C1  it 
Gli interessi maturano durante tutto il periodo considerato e di conseguenza sono direttamente proporzionali ad esso,
pertanto essi verranno conteggiati al termine del contratto.
C
0
i
M
t
I  Cit
Interesse maturato > 0
Durata t
t
Intero  anni
I
 N  0  
Ci
Decimale  anni, m, gg
Tasso d’ interesse i
i
I  M C  M  C
I
 n  0  n  1
Ct
CAPITALIZZAZIONE COMPOSTA
M  C (1  i) t
Gli Interessi maturano ogni anno e quindi M > C e l’ andamento è esponenziale, per t = 0 La curva passa per C .
Per determinare il tasso (i) e la durata (t) si parte da
(1  i)t 
M
K 0
C
Per determinare i oppure t si deve ricorrere al logaritmo
t
t...n int ero  anni
log K

log( 1  i) t....ndecimale  anni, mesi, giorni
t  1...si..ha..semplice
Si evidenzia dai grafici che t  1...si..ha..sia..semplice..che..composta.

t  1..si..ha..composta

 log K
i  ant log 
 t
Ovvero
i  10

  1  n....0  n  1

(log(
log K
)
t
1
Schema tasso periodale
Da ricordare
Tasso periodale i k dove K è il numero di periodi in 1 anno , esempio :
1
12
 6....mesi...  ...semestre
2
12
K  3  3.. periodi  .. 
 4...mesi..  .....quadrimest re
3
K  2  2... periodi  . 
Durata periodale k a
Se k = n ° periodi in 1 anno si ha la durata = k * n ° anni : esempio
3 anni = k 3 periodi. Se k = 4 (trimestre) si hanno 3 * 4 = 12 trimestri
6 anni = k 6 periodi Se k = 2 ( semestri) si hanno 6 * 2 = 12 semestri
Trasformazione di tasso periodale in tasso annuo
i  k  ik
dato tasso quadrimestrale i 3 = 2 % , k = 3 , i = ( 2*3)% = 6 %
Trasformazione di tasso annuo in tasso periodale
ik 
1
i
k
dato tasso annuo i = 4 % e periodo semestrale k = 2 si ha
i = (1/2 * 6) % = 3%
Tale relazione deriva dalla considerazione dei tassi equivalenti in capitalizzazione semplice e conseguenti passaggi
algebrici. Si ha la relazione
M  C (1  i  n)  C (1  ik  kn)
Si effettuano i passaggi algebrici ricorrendo ai principi di equivalenza
Durata è di tipo frazionario
Se la durata è di tipo frazionario occorre fare molta attenzione in quanto sono presenti mesi e giorni: per gli
anni è già stato visto e si moltiplica per k , il problema sono i mesi ed i giorni. Bisogna tener presente il periodo
che si considera (bimestre, trimestre, quadrimestre ecc ) ed i mesi che si hanno nella durata: esempio trimestre ( 3
mesi) ed i mesi sono 4 ( della durata) quindi si ha 4 = 3 + 1 = 1 trimestre + 1 mese e tale trimestre viene aggiunto a
quelli trovati con gli anni ….. Facciamo un esempio pratico: la durata effettiva è di 3 anni, 4 mesi e 13 giorni, il
periodo da considerare è il trimestre ( k = 12/3 = 4 ) si avrà quindi :
da
trimestri  ka  4  3  12  mesi..4  4  3  1  1..trimestre  1..messe che
..
12  1  13..trimestri.
per il restante tempo ( 1 mese e 13 giorni ) si considera la frazione di trimestre = 3 * 30 = 90 gg
quindi
1.mese  30...giorni  30  13  43..giorni quindi

43
 0.4777777777
90
e la durata in trimestri sarà di 13.47. Fare quindi MOLTA attenzione !!
Anche se si considera il periodo frazionato e quindi il tasso periodale le formule non mutano e neppure le
regole che si sono viste per la durata annua. La tipologia dei contratti resterà sempre la medesima ed anche gli
intervalli di validità. Attenzione solamente al fatto che si parla di bimestre, trimestre ecc e quindi di frazione di
bimestre, trimestre ecc … il punto di indifferenza per la capitalizzazione sarà di 1 periodo ( 1 trimestre..)
2