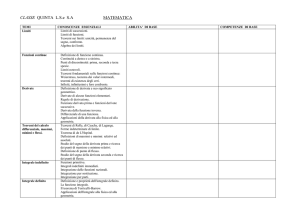
PRINCIPALI DERIVATE
PRINCIPALI PRIMITIVE
D(k)=0
D(x)=1
dx x c
x a 1
c
a 1
ax
x
a
dx
c
ln a
D(xa)=a xa-1
a
x dx
D(ax)= ax lna
D(ex)= ex
D(logax)=
e dx e
x
1
x ln a
x
c
1
x a dx ln x a c
D(sinx)=cosx
cos xdx sin x c
D(cosx)=-sinx
sin xdx cos x c
1
1 tg 2 x
cos 2 x
1
D(arsinx)=
1 x2
1
D(artgx)=
1 x2
D(tgx)=
D(f(x)+g(x))=f '(x)+g '(x)
D(k·f(x))=k·f '(x)
D(f(x) ·g(x))=f '(x) ·g(x)+f(x) ·g '(x)
D
1
f '( x)
2
f ( x)
f ( x)
D
f ( x) f '( x) g ( x) f ( x) g '( x)
2
g ( x)
g ( x)
D{f(g(x))}=f '(g(x))·g '(x)
D a f ( x ) a f ( x ) f '( x) ln a
D f ( x) f ( x)
D{ln(f(x))}=
1
f '( x)
f ( x)
f '( x)
STUDIO DI FUNZIONE
1. Insieme di esistenza
2. Limiti agli estremi di tale insieme
3. Studio del segno e delle intersezioni con gli assi
4. Calcolo derivata prima y'
y'>0 funzione crescente sugli intervalli contenuti nell'ins. Esist.
y'<0 funzione decrescente sugli intervalli contenuti nell'ins. Esist.
5. (se richiesta) Calcolo derivata seconda y"
y">0 concavità rivolta verso l'alto
y"<0 concavità rivolta verso il basso
6. Ricerca di asintoti obliqui se lim f ( x) . As. Obl. y=mx+q se
x
f ( x)
finito e diverso da zero;
x
lim f '( x) se
m lim
x
7. Calcolo
q= lim f ( x) mx finito
x
x a ,a ,a
7.1 a= estremo I.E., non infinito, in cui la funzione presenta limite finito
7.2 a appartiene ad I.E. della funzione, ma non della derivata prima
7.3 f(x)=f1(x) per x<a, f(x)=f2(x) per x>a
Esempi per punto 7:
1
1
1
7.1 f ( x) e x . Si ha: lim f ( x) 0; f '( x) e x 2 ; lim f '( x) 0 . Il diagramma in un
x 0
x x 0
intorno sinistro dello zero è dunque (si noti la tangente orizzontale):
7.2 f ( x) x . La funzione è definita per x0. La derivata prima è
1
, non definita per x=0. Si
2 x
ha lim f '( x) . Il diagramma in un intorno sinistro dello zero è quindi (si noti la tangente
x 0
verticale):
x 1( f1 (x)) x -1
7.3 f ( x) x 1
.
x 1( f 2 (x)) x 1
La funzione cambia definizione in corrispondenza di x=-1. La derivata prima è:
1 x -1
f '( x)
.
x 1
1
Al punto x= -1 la funzione arriva con tangenti diverse a seconda che la x si avvicini dalla sinistra
o dalla destra. Il diagramma in un intorno di -1 è dunque (si noti il punto angoloso):
Integrali immediati
-
1
x4
3
2
x
3
x
sin
x
dx
x3 ln x 1 cos x c
x 1
4
-
2
2
2
2 x 1 x dx 1 x 2 xdx
-
-
cos
-
3
2
2
2
sin xdx sin x sin xdx sin x (1 cos x)dx sin x sin x cos x dx cos x
1
3
2
1 x2 2 c
3
sin(2 x) 3cos x
dx ln cos 2 x 3sin x c
2
cos x 3sin x
(in quanto D( cos 2 x 3sin x )=2cosx(-sinx)-3cosx= -sin(2x)-3cosx)
2
xdx
1
1
1
1 sin(2 x)
1
1
2 cos 2 xdx (2 cos 2 x 1 1)dx (cos(2 x) 1)dx
x c sin(2 x) x c
2
2
2
2 2
4
2
cos3 x
c
3
REGOLE DI INTEGRAZIONE
1. Regola di integrazione per scomposizione
f ( x) g ( x) dx f ( x)dx g ( x)dx
da cui anche
k f ( x)dx k f ( x)dx
2. Regola di integrazione per sostituzione
f ( x)dx f ( g (t )) g '(t )dt
3. Regola di integrazione per parti
f '( x) g ( x)dx f ( x) g ( x) f ( x) g '( x)dx
Esempi di applicazione
1. Scomposizione
1
1
x2 5x 6 dx ( x 3)( x 2)dx
Non si riconosce nella funzione integranda una derivata. Scomponendo il denominatore, si notano
due fattori di primo grado. Se il denominatore fosse di primo grado, potremmo riconoscere nella
frazione la derivata di un logaritmo. Ci proponiamo quindi di spezzare la frazione nella somma di
due frazioni con denominatori di primo grado e numeratori per ora incogniti, che chiameremo A e
B:
1
A
B
A( x 2) B( x 3) Ax 2 A Bx 3B ( A B) x 2 A 3B
( x 3)( x 2) x 3 x 2
( x 3)( x 2)
( x 3)( x 2)
( x 3)( x 2)
Cerchiamo ora i numeratori incogniti in modo tale che l'ultima frazione sopra scritta sia uguale alla
1
( A B ) x 2 A 3B
prima, per ogni x reale (esclusi x=2, x=3, ovviamente!):
.
( x 3)( x 2)
( x 3)( x 2)
I denominatori sono uguali; devono quindi essere uguali anche i numeratori. Occorre quindi
imporre che il numeratore della seconda (che contiene le incognite) sia uguale ad 1 per ogni x. Deve
quindi essere eliminato l'addendo contenente x; questo si ottiene imponendo che il suo coefficiente
sia uguale a 0. Il numeratore della seconda frazione diventa quindi: -2A-3B e, perché le due frazioni
siano uguali, esso deve essere uguale ad 1. Abbiamo quindi ottenuto 2 condizioni che ci permettono
di determinare A e B:
A B 0
B A
B 1
, da cui:
.
;
2 A 3B 1
2 A 3 A 1 A 1
Si ha quindi:
1
1
1
1
x2 5x 6 dx ( x 3)( x 2)dx x 3 dx x 2 dx ln x 3 ln x 2 c
Si noti che si è utilizzata la scomposizione della frazione al fine di utilizzare la regola di
integrazione per scomposizione.
2. Sostituzione
Si debba calcolare l'integrale
1 x 2 dx . Non riconosciamo nella funzione integranda una derivata
in quanto, perché fosse la derivata di una potenza di 1-x2 dovrebbe essere presente un fattore -2x
(derivata di 1-x2) che invece non abbiamo. Se effettuiamo la sostituzione x=sin t ed applichiamo la
regola di integrazione per sostituzione, otteniamo:
1 x 2 dx 1 sin 2 x cos xdx
1
1
cos 2 xdx se cosx 0 sin(2 x) x c
4
2
cos 2 x cos xdx cos x cos xdx
2
1
cos
xdx
se
cosx<0
sin(2 x) 1 x c
4
2
(vedi integrali immediati per l'ultimo passaggio).
Spesso si usa la regola di integrazione per sostituzione in modo diverso. Si consideri ad esempio
ln 2 x 2ln x
l'integrale
dx .
x
Qui è evidente che la variabile rispetto alla quale è scritta la funzione integranda è il logaritmo, del
quale è anche presente la derivata 1/x. Se allora poniamo t=lnx, per completare la sostituzione
dobbiamo differenziare i due membri della relazione. Ricordando che il differenziale di una
1
funzione è il prodotto della sua derivata per il differenziale della variabile, si ha: 1 dt dx , da cui
x
2
3
ln x 2ln x
t
1
dx t 2 2t dt t 2 c ln 3 x ln 2 x c
x
3
3
3. Integrazione per parti
- xe x dx xe x 1 e x dx xe x e x c
-
x cos xdx x sin x 1 ( sin x)dx x sin x cos x c
-
ln xdx 1 ln xdx x ln x x x dx x ln x x c
-
x e dx x e 2x e dx x e
1
2 x
2 x
x
2 x
2 xe x 2e x dx x 2 e x 2 xe x 2e x c
Attenzione! Se la regola di integrazione per parti si deve applicare ripetutamente, è indispensabile
ripetere le scelte effettuate nelle precedenti applicazioni. Nell'integrale appena calcolato si è scelto
di considerare ex come f ', sia nella prima che nella seconda applicazione della regola.
Se si cambiano le scelte, si ritorna al punto di partenza! Si ha infatti:
2 x
2
x
2 x
2 x
x
2 x
2 x
2
x
x e dx x e 2x e dx x e x e x e dx , ossia x e dx x e dx
-
e
x
sin xdx e x sin x e x cos xdx e x sin x e x cos x e x ( sin x)dx .
Si noti che, anche in questo esempio, pur avendo ripetuto la scelta di considerare ex come f ', si è
ritrovato l'integrale di partenza al secondo membro. A differenza di quanto successo nell'esempio
precedente, in questo caso l'integrale che si deve calcolare compare al secondo membro preceduto
dal segno -. Si ha cioè:
x
x
x
x
x
x
x
e sin xdx e sin x e cos x e ( sin x)dx e sin x e cos x e sin xdx .
Da questa relazione, ignorando il secondo termine della catena di uguaglianze, si ottiene:
e x sin x e x cos x
2 e x sin xdx e x sin x e x cos x c , ossia e x sin xdx
c.
2
Integrazione delle funzioni del tipo f ( x)
1
ax bx c
2
Il primo caso è già stato considerato come applicazione della regola di integrazione per
scomposizione. E' il caso in cui il delta sia positivo, e quindi il trinomio possiede due radici reali
1 , 2 e si può scomporre in fattori: ax 2 bx c a( x 1 )( x 2 ) .
Restano i casi in cui il delta sia nullo o negativo.
Se il delta è nullo, ci sono due radici coincidenti e il trinomio può essere scritto come
ax 2 bx c a( x )2
In questo caso l'integrale diventa:
dx
dx
1
1 ( x )1
1
2
(
x
)
dx
c
c
ax2 bx c a( x )2 a
a
1
a( x )
Se il delta è negativo, il trinomio non ha radici reali e può essere scritto nella forma
2
2
c
b
b2
c
b
4ac b 2
2 b
2
ax bx c a x x a x
a
x
a
a
2a 4a 2 a
2a
4a 2
Si noti che nell'ultima parentesi quadra si è ottenuta la somma di due quantità sicuramente positive
(un quadrato e il delta, che era negativo, cambiato di segno e diviso per un numero positivo). Con
opportune trasformazioni (raccoglimento a fattor comune e introduzione di coefficienti nella
parentesi elevata al quadrato) la quantità in parentesi quadra può essere scritta nella forma
1 (ax b)2 , che posta al denominatore di una frazione, fa pensare alla derivata della funzione arco
tangente.
Si consideri il seguente semplice caso:
dx
dx
dx
x2 4 x 5 x2 4 x 4 1 1 ( x 2)2 artg ( x 2) c
Si consideri ora il seguente esempio più complesso:
dx
dx
dx
dx
4
dx
2
x 2 x 1 1 2 1 1 2 3 3 4 1 2 3 2
1
x 1
x 1
x 1
x
2 4
2 4
4 3
2
2
3
2
1
artg x
2
2
4
2
1
3
c
artg x c
2
3
2
3
3
3
Esercizi proposti
sin x dx
x
2
1
dx
3x 4
cos
3
xdx
ln x
dx
x
(per parti e/o per sostituzione, ponendo t= x )
(per scomposizione)
(immediato)
INTEGRALE DEFINITO
Sia f una funzione continua sull'intervallo [a,b], chiuso e limitato, che assume su [a,b] valori
positivi. Il problema da risolvere è il calcolo dell'area A della regione piana racchiusa fra il
diagramma della funzione, l'asse delle x e le due rette verticali di equazione x=a e x=b (tale regione
viene chiamata trapezoide, per la sua somiglianza con un trapezio rettangolo)
Il problema è di facile soluzione quando la funzione è costante, perché il trapezoide diventa un
rettangolo, o quando la funzione è una retta obliqua, perché il trapezoide diventa un trapezio. Se
invece si ha una curva qualunque, non si può ricorrere alla geometria elementare.
Si procede allora mediante un'approssimazione dell'area, costruendo due insiemi di rettangoli.
Costruiamo prima di tutto una partizione dell'intervallo [a,b] così definita:
a x0 x1 x2 ... xn b , individuando i sottointervalli Ei=[xi-1,xi], i=1,1,…,n.
La f è continua su [a,b] e quindi lo è anche su ogni intervallino Ei, quindi possiede su Ei minimo mi
e massimo Mi.Costruiamo su ogni intervallino i rettangoli che hanno come base l'intervallino e
come altezze il minimo e il massimo, rispettivamente. Nella figura si osservano in rosso due
rettangoli che hanno per altezza il massimo e 4 rettangoli che hanno per altezza il minimo.
L'area di tali rettangoli è: (xi-xi-1)·mi e (xi-xi-1)·Mi .
Consideriamo ora la somma inferiore n-esima (somma delle aree dei rettangoli aventi per altezza i
minimi):
sn m1 ( x1 x0 ) m2 ( x2 x1 ) ... mn ( xn xn1 )
e la somma superiore n-esima ((somma delle aree dei rettangoli aventi per altezza i massimi):
Sn M1 ( x1 x0 ) M 2 ( x2 x1 ) ... M n ( xn xn1 )
Per come le abbiamo costruite, si ha la relazione:
s n A Sn .
Osserviamo che l'approssimazione migliora aumentando il numero dei punti.
Pensiamo ad esempio a quanto succede se in uno degli intervallini individuati si aggiunge un
punto
la somma inferiore aumenta di tutto il rettangolo evidenziato
in rosso, perché sulla seconda parte dell'intervallo si ha un minimo maggiore che sulla prima,
mentre la somma superiore diminuisce del rettangolo evidenziato in blu, perché sulla prima parte
dell'intervallo si ha un massimo minore.
Dunque aumentando il numero degli intervalli si ha:
s n sn1 A Sn1 Sn
Pur di mantenere abbastanza uniformi le dimensioni dei sottointervalli Ei, si avrà
lim sn A lim S n
n
n
b
Tale area sarà indicata con il simbolo A= f ( x)dx
a
Proprietà dell'integrale definito
a
1.
f ( x)dx 0
a
2.
a
b
b
a
f ( x)dx f ( x)dx
b
b
a
a
3. kf ( x)dx k f ( x)dx
b
b
b
4. ( f ( x) g ( x))dx f ( x)dx g ( x)dx
a
5.
a
a
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
6. se in [a,b] vale f ( x) g ( x) , vale anche
b
7.
b
f ( x)dx
a
a
f ( x) dx
b
b
a
a
f ( x)dx g ( x)dx
Alcune equazioni differenziali ordinarie
1. A variabili separabili: y ' p( x)q( y )
1.a
se y=k è soluzione di q(y)=0, è anche soluzione dell'equazione differenziale, perché annulla
entrambi i membri.
1.b
se q(y)0, con la notazione di Leibnitz:
dy
dy
dy
p ( x)q ( y )
p( x)dx
p( x)dx c
dx
q( y)
q( y)
2. Lineari del primo ordine: y ' p ( x) y q ( x)
p ( x ) dx
soluzione y e
q(x)e
p ( x ) dx
dx c
3. Lineari del II ordine a coefficienti costanti: ay '' by ' cy b( x)
3.a
equazione omogenea: ay '' by ' cy 0
equazione caratteristica: a 2 b c 0
se eq. caratteristica ha due soluzioni reali e distinte, 1 e 2 , l'integrale
generale è y c1e1 x c2e 2 x
se eq. caratteristica ha due soluzioni reali coincidenti, l'integrale generale è
y c1e1 x c2 xe1 x
se eq. caratteristica ha soluzioni complesse
b b2 4ac
, con b2 4ac 0 , l'integrale generale è
2a
b
x
y e 2 a c1 sin
x c2 cos
x
2
a
2
a
equazione non omogenea
L'integrale generale è la somma dell'integrale generale dell'equazione omogenea e di
un integrale particolare della non omogenea.
se b( x) pn ( x) e y compare nell'equazione, si cerca y qn ( x) ;
3.b
se y non compare, ma compare y', si cerca y qn 1 ( x)
se b( x) eax e non è soluzione dell'equazione caratteristica, si cerca
y Ae ax
se è soluzione dell'equazione caratteristica, si cerca y Axeax
o y Ax 2e ax a seconda che sia radice di molteplicità
1o2