appello-22-02

CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Appello di FISICA, 22 febbraio 2011
1) Un autocarro con massa a pieno carico pari a M = 1.1 104 kg percorre con velocità costante vi = 72
km/h, un tratto stradale rettilineo. A causa della nebbia la visibilità è di soli d = 80 m.
Improvvisamente compare dalla nebbia una macchina ferma di massa m = 900 kg.
Supponendo che il tempo di reazione dell’autista sia trascurabile si calcoli:
a) la minima decelerazione a che permetterebbe all'autocarro di fermarsi ed evitare l’urto e, invece, la
velocità vf al momento dell’urto con l’auto se il conducente ha esercitato una forza frenante costante
F =2.0·104 N;
b) la velocità v con cui autocarro ed auto proseguono assieme appena dopo l’urto, che è supposto
completamente anelastico.
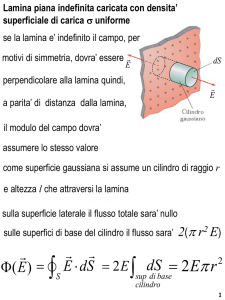
2) Una lamina metallica piana, infinitamente estesa, è uniformemente carica con densità di carica
superficiale  = + 2.0  10-12 C/m2. A distanza d = 1 m dalla lamina, lungo l’asse x positivo supposto
perpendicolare alla lamina e con origine sulla lamina, è posta una carica puntiforme positiva pari a Q
= + 4.0  10-12 C. Determinare:
a) il campo elettrico nel punto P a distanza d/2 dalla lamina lungo l’asse x positivo, indicandone modulo,
direzione e verso;
b) il punto S dell’asse x ove è possibile porre una carica q positiva, in equilibrio.
[ Note: 0 = 8.85 10-12 C2/Nm2 ]
3) Una cisterna cilindrica riempita di acqua, alta H = 4 m e del diametro D = 1 m, poggia a terra ed ha un
forellino del diametro d=1 cm ad una altezza h = 1 m dal suolo. Supponendo che l’acqua possa essere
considerata un fluido ideale, in moto stazionario e irrotazionale, si calcoli:
a) il rapporto fra le velocità dell’acqua alla superficie libera della cisterna e all’uscita dal forellino e la
velocità iniziale di deflusso dell’acqua dal forellino, facendo le opportune approssimazioni;
b) il tempo necessario per riempire un secchio di 5 litri con l’acqua che esce dal forellino.
4) Quattro moli di gas perfetto biatomico, inizialmente nello stato A caratterizzato dalla pressione pA
= 4 atm e VA = 20 litri, compiono una trasformazione ciclica costituita da due trasformazioni isobare
AB e CD e due isocore BC e DA. Sapendo che lo stato C è caratterizzato da una pressione pC = 2 atm
ed un volume VC = 60 litri,
a) si disegni il ciclo nel piano p-V e si calcoli la temperatura del gas nei quattro punti A, B, C e D;
b) si calcolino il lavoro fatto in un ciclo e i calori scambiati nelle varie trasformazioni;
[ Nota: R= 8.31 J/Kmole ]
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI. SOSTITUIRE I
VALORI NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI MISURA. Testi, soluzioni ed esiti
alle pagine: www2.fisica.unimi.it/bettega/ (AD), qinf.fisica.unimi.it (EN), www.mi.infn.it/~sleoni (OZ)
SOLUZIONE ESERCIZIO 1
a) a > 1/2 vi2/d =2.5 m/s2
vf2 = vi2 - 2 F d /M
da cui segue:
vf = 10.4 m/s = 37.4 km/h
b) v= vf × M/(M+m) = 9.61 m/s = 34.6 km/h
SOLUZIONE ESERCIZIO 3
a) Indicata con V la velocità del fluido in corrispondenza alla superficie libera della cisterna che ha
area S, e con v quella in corrispondenza del forellino di uscita, che ha area s, si ha :
VS=vs
v.
e pertanto V/v = s/S = ( 5 10–3 )2 / ( 5 10–1 )2 = 10 – 4 , quindi V è trascurabile rispetto a
La velocità iniziale di deflusso si calcola utilizzando il teorema di Bernoulli applicato ai punti della
superficie libera della cisterna e a quelli del forellino di uscita :
P + ½ V2 +  g H = p + ½ v2 +  g h dove P e p sono i valori della pressione nelle due posizioni,
con P = p e  è la densità del fluido . Inoltre il termine ½ V2 può essere trascurato. Si ha quindi:
 g H = ½ v2 +  g h da cui :
v = (2 g ( H-h) ) ½ = 7.7 m/s
b) Poiché la portata volumetrica Q = vs = 604.8 10-6 m3 / s = 0.6 litri /s, per riempire il secchio di 5
litri occorrono 8.3 s
SOLUZIONE ESERCIZIO 2
a) Il campo elettrico nel punto nel punto P = (d/2,0) è dato dalla somma dei campi prodotti in P dalla lamina e
dalla carica. I campi prodotti dalla lamina e dalla carica sono entrambi diretti lungo l'asse x ma con segno
opposto (positivo il campo della lamina, negativo quello della carica Q). Pertanto:



E ( P )  E ( P )  EQ ( P)
 
1
Q 

i
i
2 0
40 (d / 2) 2
12
2  10 12
N
N
9 4  10

i

9

10
i
2  (8.85  10 12 ) C
(0.5) 2 C
N
N
N
 0.113 i  0.144 i  0.03 i
C
C
C
Il campo E in P è diretto lungo l'asse x con verso opposto all'asse.
b) L'unica regione dell'asse x ove è possibile trovare un punto di equilibrio per una carica q è quella compresa
tra la lamina e la carica, dato che nelle regioni x > d e x < 0 i due campi (della lamina e della carica) hanno
verso concorde.
Indicata con x la distanza dalla carica Q, dalla condizione di equilibrio tra le forze segue che:
F  FQ
q

1 qQ

2 0 40 x 2
x2 
Q 1
 2
x
Q 1

 2
4  10 12 1
m  0.56 m
2  10 12 2
Si trova quindi che la distanza OS del punto S dall'origine è
OS = d-x = 0.44 m
SOLUZIONE ESERCIZIO 4
a) TA= = 243.8 K; TB=731.4 K; TC=365.7 K; TD=121.9 K;
b) L = area del rettangolo = (VB-VA)×(pB-pA) = 81.04 102 J
QAB = n Cp (TB-TA) = 56.7 kJ;
QBC = n Cv (TC-TB) = -30.4 kJ;
QCD = n Cp (TD-TC) = -28.4 kJ;
QDA= n CV (TA-TD) = 10.1 kJ.