File - Massimo Catella

Probabilità di un evento composto (eventi indipendenti)
Un evento composto è costituito dalla sequenza di almeno due eventi semplici.
Esempio: consideriamo due monetine e calcoliamo la probabilità che esca testa su entrambe le monetine.
L’evento consiste nel lanciare una prima monetina, controllare se è uscita testa o croce E poi si lancia la seconda
monetina e si controlla ancora se è uscita testa o croce. In un evento composto vengono allora eseguiti almeno due
“gesti”, mentre in evento semplice si esegue un solo gesto.
Un evento composto è caratterizzato dalla presenza del connettivo E che unisce due eventi semplici.
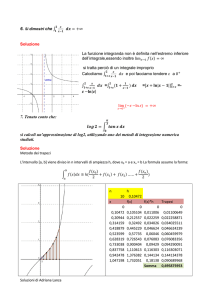
Per calcolare la probabilità di un evento composto si utilizza un diagramma ad albero.
A fianco di ogni lancio è indicata
la probabilità che esca testa o croce
in un singolo lancio di monetina
Sia che esca testa sia che esca
croce, la probabilità è
1
2
Il singolo lancio è un evento
semplice.
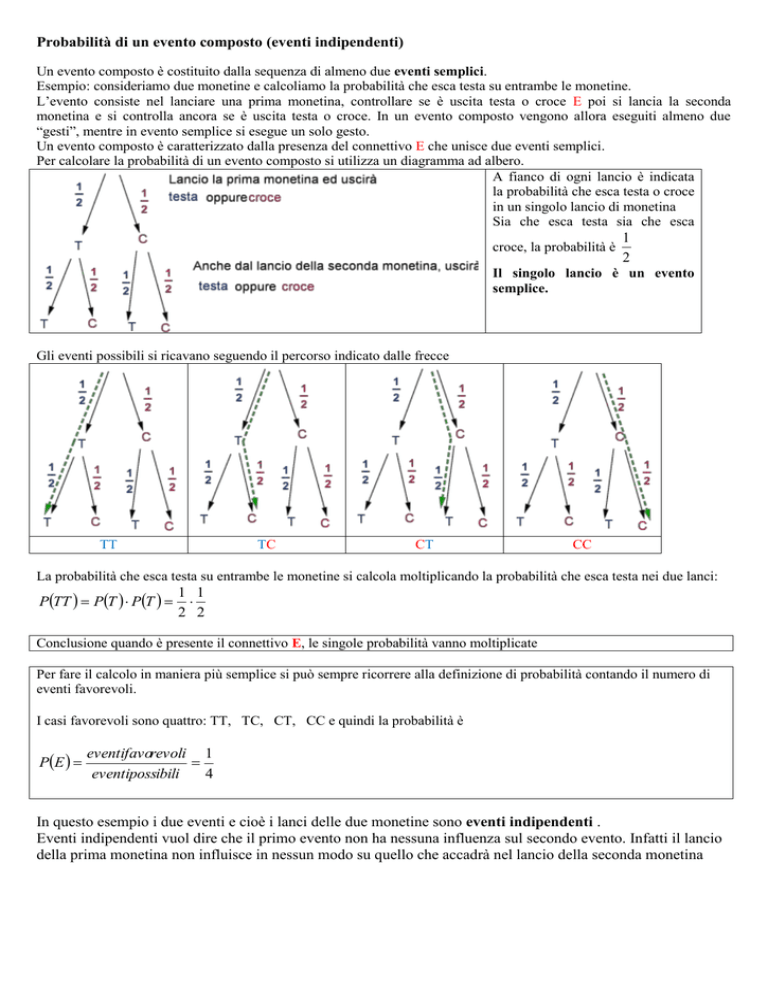
Gli eventi possibili si ricavano seguendo il percorso indicato dalle frecce
TT
TC
CT
CC
La probabilità che esca testa su entrambe le monetine si calcola moltiplicando la probabilità che esca testa nei due lanci:
PTT   PT   PT  
1 1

2 2
Conclusione quando è presente il connettivo E, le singole probabilità vanno moltiplicate
Per fare il calcolo in maniera più semplice si può sempre ricorrere alla definizione di probabilità contando il numero di
eventi favorevoli.
I casi favorevoli sono quattro: TT, TC, CT, CC e quindi la probabilità è
P E  
eventifavorevoli 1

eventipossibili
4
In questo esempio i due eventi e cioè i lanci delle due monetine sono eventi indipendenti .
Eventi indipendenti vuol dire che il primo evento non ha nessuna influenza sul secondo evento. Infatti il lancio
della prima monetina non influisce in nessun modo su quello che accadrà nel lancio della seconda monetina