La probabilità condizionata

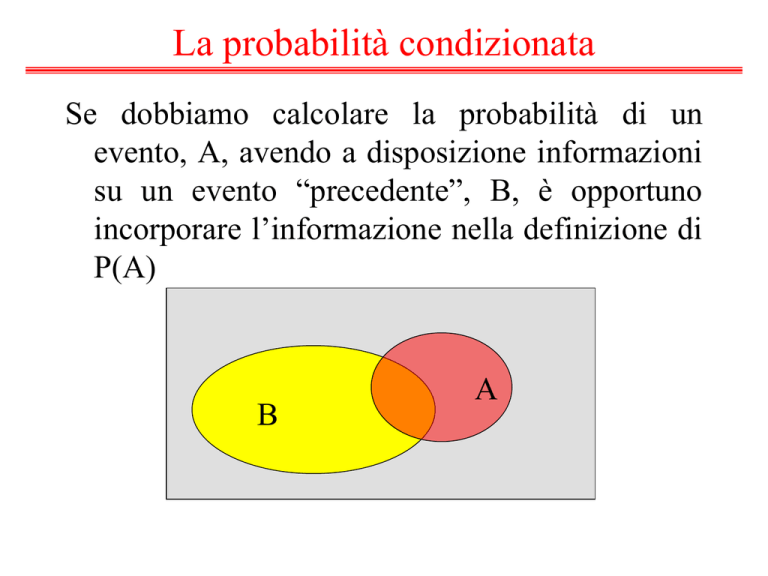
La probabilità condizionata
Se dobbiamo calcolare la probabilità di un
evento, A, avendo a disposizione informazioni
su un evento “precedente”, B, è opportuno
incorporare l’informazione nella definizione di
P(A)
B
A
La probabilità condizionata
Definiamo la probabilità di A condizionata a B:
P(A  B)
P(A|B)=
P(B)
• L’evento B diventa il nuovo spazio campionario
di riferimento
Esempi
•
–
–
–
–
–
–
–
Lancio di due monete.
Ω = {(T,T); (T,C);(C,T); (C,C) }
A={2° lancio è T},
B={1° lancio è T}
P(A) = P(T,T) + P(C,T) = 1/2
P(B) = P(T,T) + P(T,C) = 1/2
P(A∩B) = P(T,T) = 1/4
P(A|B) = P(A∩B)/P(B) = 1/2
Esempi
• Lancio di un dado.
– Ω = {1,2,3,4,5,6}
A={6}, B={2,4,6}, C={1,3,5}, D={1,3}
P(A|B) = 1/3
P(A|C) = 0
P(D|C) = 2/3
Esempi
In uno spazio campionario si ha
P(A1) = 1/3 , P(A2)= ¼ e P(A1  A2) =1/6
Verificare che
1. P(A1| A2) = 2/3
2. P(A2| A1) = 1/2
3. P(Ā2 | A1) = 1/2
4. P(A2 | Ā1) = 1/8
5. P(Ā2 | Ā1) = 7/8
Esempi
Sia  = [0;1] (l’int. 0,1), per un evento A ,
P(A) =  dx
A
Se A=[0; 0,5], B=[0,3; 0,8], C=[0,7; 1]
0.5
 dx
P(A|B) =
0.3
0.8
 dx
0.3
0.2

, P(A|C) =0
0.5
Regola moltiplicativa e indipendenza
• Si noti che dalla definizione:
P (A  B) = P(A) P(B|A) = P(B) P(A|B)
• Due eventi si dicono indipendenti se il
verificarsi di B non influenza la probabilità di
A e viceversa
P (A|B) =P(A)
P(B|A) = P(B)
• Vale quindi la relazione
P(A  B) = P(A) P(B)
Il ricorso alla regola moltiplicativa spesso permette di calcolare
più agevolmente la probabilità di intersezioni di eventi
Esempio
Da un mazzo di 52 carte se ne estraggono due in
sequenza, senza riposizione . Determinare la
probabilità che la prima estratta sia una carta di
cuori (A1) e la seconda estratta sia una carta di fiori
(A2)
La probabilità cercata è P(A1∩ A2)
P(A1) = 13/52,
P(A2 |A1) = 13/51,
P(A1∩ A2) = P(A2 |A1) P(A1) = 132/(52∙51)
Indipendenza
Quando vale la relazione
P(A  B) = P(A) P(B)
si dice che gli eventi A e B sono indipendenti.
L’indipendenza permette di calcolare probabilità
congiunte da probabilità di singoli eventi
P( A  B  C) = P(A)P(B  C) = P(A)P(B)P(C)
P(A B) = P(A) + P(B) – P(A)P(B)
Esempio
Lancio di una moneta due volte:
 = {(T,T), (T,C), (C,T), (C,C)}
Definiamo:
A = {1° lancio T} = {(T,T), (T,C)}
B = {2° lancio T} = {(T,T), (C,T)}
da cui
A  B = {(T,T)}
P(A  B) = 1/4 = (1/2)(1/2) = P(A) P(B)
Teorema di Bayes
• Sia A1, A2 , ... Ak una partizione di , cioè
A1 A2  ... Ak =  , Ai Aj = , i j
• Dato un qualsiasi evento B ,
P  Ai   P B | Ai 
P  Ai | B  
P  A1  P B | A1  ...  P  Ak   P B | Ak 
A1
A2
B
A3
A4
Teorema di Bayes
Si noti che possiamo sempre scomporre
P  B   P  A1   P  B | A1   ...  P  Ak   P  B | Ak 
Poiché
P  B   P  B  A1   ...  P  B  Ak 
Esempio
Uno studente deve sostenere un esame.
Se studia passa con probabilità 99 %, ma se va alla
festa da ballo la sera prima la sua probabilità di
promozione si riduce al 50 %.
Decide di andare alla festa se esce testa lanciando una
moneta equa.
Il giorno dopo egli supera l'esame.
Qual è la probabilità che sia andato a ballare?
Si considerino gli eventi:
E = passa l'esame,
A = va alla festa,
I dati a disposizione sono:
P( E | Ā)= 0.99, P( E | A) = 0.50, P(A) = P(Ā)= 0.5
Da cui
P( E | A) P( A)
P( A | E ) 
P( E | A) P( A)  P( E | A) P( A)
0.5  0.5

 0.336
0.5  0.5  0.5  0.99