IL LANCIO DI DUE DADI
PROBABILITA’ E FREQUENZA
DATI E PREVISIONI
I DADI
I dadi tradizionali, utilizzati dalla
maggior parte dei giochi, sono cubi con
le facce marcate con i numeri naturali
da 1 a 6.
Per ottenere un valore casuale, si fa
rotolare il dado su una superficie piana,
e convenzionalmente viene preso in
considerazione come "risultato" il
valore che si viene a trovare sulla faccia
rivolta verso l'alto quando il dado
termina il proprio movimento.
L'evento così ottenuto si può
considerare casuale solo se il
movimento impartito inizialmente al
dado è sufficiente a farlo rotolare e
rimbalzare in modo imprevedibile.
LA PROBABILITA’
lim
DEFINIZIONE FREQUENTISTA
DEFINIZIONE CLASSICA
La probabilità di un evento è il
limite della frequenza (relativa)
dei successi, cioè del verificarsi
di un evento, quando il numero
delle prove, n, tende
all’infinito.
La probabilità di un evento è il
rapporto tra il numero di casi
favorevoli (al verificarsi
dell’evento) e il numero di casi
possibili, purché questi numeri
siano ugualmente possibili.
numero di casi favorevoli
n->∞
n
numero di casi favorevoli
numero di casi possibili
•la probabilità di un evento aleatorio è un
numero compreso tra 0 e 1;
•la probabilità dell'evento certo è pari a 1;
•la probabilità del verificarsi di uno di due eventi
incompatibili, ovvero di due eventi che non
possono verificarsi simultaneamente, è pari alla
somma delle probabilità dei due eventi.
LA FREQUENZA
In statistica si definiscono due tipi di frequenze:
•FREQUENZA ASSOLUTA: è il numero di volte che si
verifica un evento.
•FREQUENZA RELATIVA: è il rapporto tra la
frequenza assoluta e il numero di prove eseguite;
viene misurata con un numero decimale compreso
tra 0 e 1, o in percentuale.
PROBABILITA’ vs FREQUENZA
La frequenza e la probabilità sono due concetti del tutto
diversi fra loro:
• La probabilità classica va calcolata "a priori"
cioè prima che l'evento accada;
• La frequenza va calcolata "a posteriori" e dopo
un numero congruo di prove, cioè dopo che gli
eventi sono accaduti.
Anche la frequenza relativa, come la probabilità, è un
numero compreso fra 0 ed 1, però un valore di
frequenza pari a zero non implica che l'evento sia
impossibile, così come un valore uguale a uno non
implica che l'evento sia certo.
PREVISIONI
Prima di passare al lancio dei dadi è possibile fare
delle previsioni sul numero di casi favorevoli e sulla
probabilità di uscita di ogni numero.
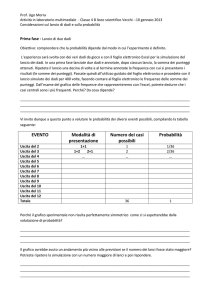
Come suggerito dalla seguente tabella, il numero che
presenta probabilità di uscita maggiore è il numero
sette, perché si ottiene da sei diverse combinazioni.
TABELLA 1
Le modalità di presentazione dei diversi numeri sono state disposte in modo da
formare un rombo. Agli estremi della sua diagonale maggiore vi sono le
combinazioni che danno rispettivamente i numeri due e 12 (una sola modalità),
mentre sulla diagonale minore sono disposte le combinazioni che danno il numero
7 (massimo delle modalità).
400 LANCI DI DUE DADI
DATI SPERIMENTALI
Numero
2
3
4
5
6
7
8
9
10
11
12
Totale
Freq. Assolute Freq. Relative Percentuale
15
0,0375
3,75%
19
0,0475
4,75%
28
0,07
7%
43
0,1075
10,75%
52
0,13
13%
59
0,1475
14,75%
65
0,1625
16,25%
52
0,13
13%
34
0,085
8,50%
23
0,0575
5,75%
10
0,025
2,50%
400
1
100,00%
Istogramma delle frequenze
Frequenza assoluta
70
60
50
40
30
20
10
0
2
3
4
5
6
7
Numero
8
9
10
11
12
Dall’istogramma
ottenuto osserviamo che
le frequenze più alte
corrispondono ai numeri
che si ottengono con il
maggiore numero di
combinazioni. Tuttavia,
contrariamente alle
aspettative, il picco
massimo cade in
corrispondenza del
numero 8.
Anche gli altri dati non
rispecchiamo
esattamente le
previsioni della Tabella 1.
Le discrepanze tra i
risultati ottenuti e le
previsioni sono
probabilmente dovute al
limitato numero di lanci
o………a dadi truccati.
FOGLIO ELETTRONICO EXCEL
PER LA GENERAZIONE CASUALE DEI LANCI
Simulazione dell’esperimento
Frequenza
GENERAZIONE CASUALE DI 400 LANCI
Evento
Anche nella simulazione dei 400 lanci le
aspettative non sono del tutto rispettate:
Le frequenze del numero 6 e del numero 7
raggiungono lo stesso valore;
Il numero 8, nonostante abbia una
probabilità di uscita maggiore rispetto
a quella dei numeri 5, 9 e 10, è meno
frequente.
PROVIAMO CON LA GENERAZIONE CASUALE DI 600 LANCI
Frequenza
GRAFICO RELATIVO A 600 LANCI
Evento
le previsioni sono quasi esattamente rispettate.
GENERAZIONE CASUALE DI 600 LANCI
2
3
4
5
6
7
8
9
10
11
12
12
26
43
57
84
110
82
75
61
37
13
600
0,02
0,043333
0,071667
0,095
0,14
0,183333
0,136667
0,125
0,101667
0,061667
0,021667
2,00%
4,33%
7,17%
9,50%
14,00%
18,33%
13,67%
12,50%
10,17%
6,17%
2,17%
Simulare il lancio di due dadi con Excel
La funzione fondamentale che useremo è
CASUALE() che dà come risultato un numero
casuale compreso fra 0 e 1 (estremi esclusi).
Notare che fra le parentesi non va scritto nulla.
Provate a scrivere "=CASUALE()" in una cella di
Excel e osservate il risultato. Se premete il tasto
F9 il risultato viene ricalcolato ed otterrete ogni
volta un numero diverso.
La distribuzione dei numeri generati da
CASUALE() è uniforme: questo significa che se
scegliamo un intervallo all'interno di (0, 1) e
generiamo poi molti numeri casuali, la
percentuale
dei
numeri
che
cadono
nell'intervallo
dato
sarà
proporzionale
all'ampiezza dell'intervallo stesso. Ad esempio:
se genero molti numeri, il 50% di essi sarà
compreso fra 0 e 0,5, il 10% sarà compreso fra
0,6 e 0,7, ecc.
CASUALE() genera un numero decimale fra 0 e 1, ma
noi vogliamo simulare il lancio di un dado e quindi
vogliamo generare un numero casuale intero compreso
fra 1 e 6. Per far questo è sufficiente moltiplicare il
risultato di CASUALE() per 6 e poi prendere la parte
intera (scartando cioè le cifre decimali): il risultato sarà
un numero compreso fra 0 e 5, a cui aggiungeremo 1
per ottenere ciò che interessa a noi. Quindi basta
scrivere in una cella di Excel
=INT(6*CASUALE())+1
per ottenere il risultato voluto: provate a farlo e
controllate premendo F9 che funzioni nel modo
corretto.
Vogliamo ora simulare 1000 lanci di due dadi.
Per fare ciò scriviamo "=INT(6*CASUALE())+1" in
una cella (A5 in figura) e poi facciamo la stessa
cosa nella colonna accanto: nelle due colonne
abbiamo così simulato il lancio di due dadi. Nella
terza colonna calcoliamo la somma dei due dadi:
nella cella C5 in figura scriveremo "=A5+B5".
Adesso selezioniamo le tre caselle e trasciniamo
verso il basso (utilizzando il riempimento
automatico) di mille posti. Nella figura, ad
esempio, sono state occupate le celle da A5 a
C1004.
Ora possiamo calcolare le frequenze dei possibili
risultati (da 2 a 12) come già spiegato nella
scorsa lezione. Poi rappresentiamo il risultato in
un istogramma. Premete F9 e osservate come
variano i risultati e il grafico. Dividendo le
frequenze ottenute per 1000 otteniamo una
stima della probabilità che esca un certo
risultato lanciando due dadi.
Quali dovrebbero essere le probabilità
teoriche?