File

CIRCUITI OSCILLANTI
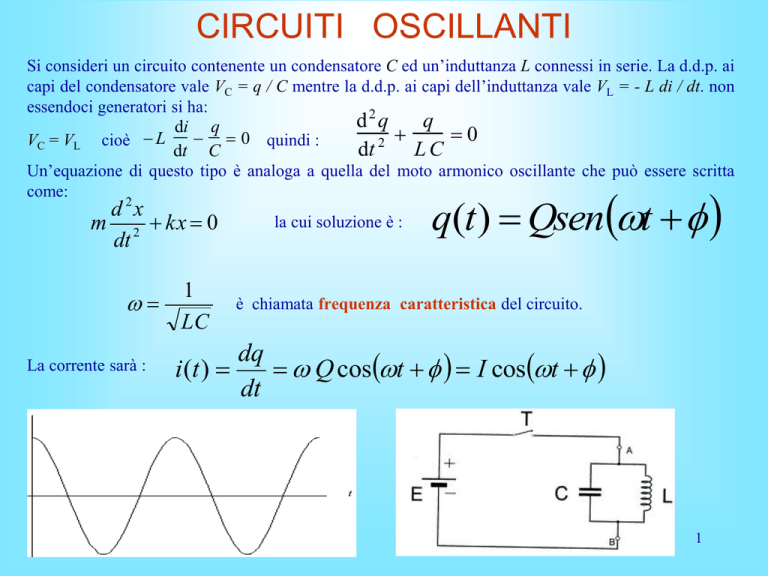
Si consideri un circuito contenente un condensatore C ed un’induttanza L connessi in serie. La d.d.p. ai
capi del condensatore vale VC = q / C mentre la d.d.p. ai capi dell’induttanza vale VL = - L di / dt. non
essendoci generatori si ha:
2
d
q
q
di q

0
  0 quindi :
VC = VL cioè  L
dt 2 L C
dt C
Un’equazione di questo tipo è analoga a quella del moto armonico oscillante che può essere scritta
come:
d 2x
m 2  kx  0
dt

La corrente sarà :
1
LC
la cui soluzione è :
q(t )  Qsent   
è chiamata frequenza caratteristica del circuito.
dq
i (t ) 
  Q cost     I cost   
dt
q
Q
t
1
Carica, corrente in circuiti LC (ideale)
(a)Condensatore completamente
carico, i=0
(b)
Condensatore in
scarica, i aumenta
(c)
Condensatore
completamente scarico, i=imax
(d)
Condensatore in carica,
i diminuisce
(e)
Condensatore
completamente carico ma con
polarità opposta rispetto ad (a),
i=0
(f)Condensatore in scarica, i
aumenta ma nel verso opposto
rispetto a (b)
(g)
Condensatore
completamente scarico, i=imax
(h)
Condensatore in carica,
i diminuisce
2
http://www.ba.infn.it/~fisi2005/a
nimazioni/simulazione012.html
3
Analogia elettricità - meccanica
Il circuito oscillante LC ha una stretta analogia con l’oscillatore meccanico studiato in
meccanica. L’equazione dell’energia dell’oscillatore meccanico può essere scritta come:
2
1 2 1 2
d 2q 1
d
x
U  U cin  U m  mv  kx  cost derivando si ha: m 2  kx  0 L 2  q  0
dt
C
2
2
dt
la cui soluzione è formalmente analoga a quella vista per la carica nel circuito LC, salvo
una diversa definizione della pulsazione . Anche nell’oscillatore meccanico, pertanto,
avviene l’oscillazione dell’energia tra l’energia potenziale insita nel blocco e l’energia
potenziale della molla.
4
Oscillazioni smorzate in circuito RLC (reale)
L’inserzione di una resistenza R in serie ad un circuito LC ha come conseguenza che l’energia
elettromagnetica totale non è più costante, poiché vi è una perdita di energia per effetto Joule nella
resistenza stessa. Questo si può vedere osservando in un oscilloscopio la curva della corrente in un
circuito RLC serie. L’equazione di questo circuito è:
d 2q
dq 1
L 2 R  q0
dt
dt C
La soluzione di questo circuito RLC serie è :
q  Qe
R t
2L
cos ' t   
Tale espressione descrive un moto oscillatorio smorzato
 R
'  2   
 2L 
2
5