Resistori - Docenti.unina

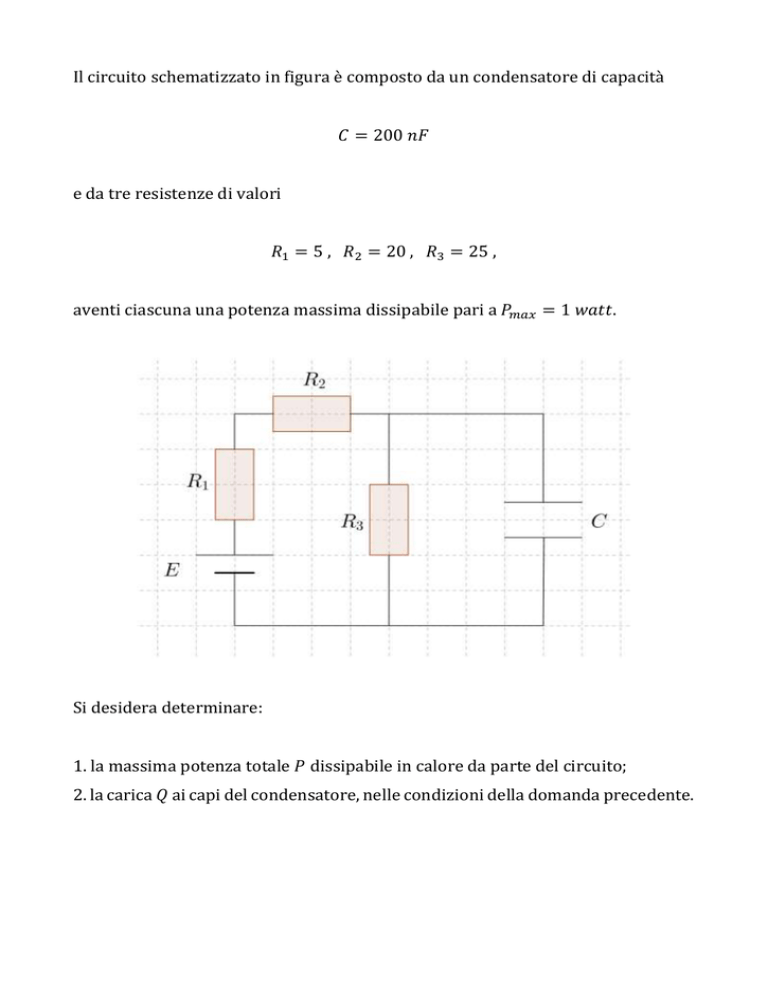
Il circuito schematizzato in figura è composto da un condensatore di capacità
𝐶 = 200 𝑛𝐹
e da tre resistenze di valori
𝑅1 = 5 , 𝑅2 = 20 , 𝑅3 = 25 ,
aventi ciascuna una potenza massima dissipabile pari a 𝑃𝑚𝑎𝑥 = 1 𝑤𝑎𝑡𝑡.
Si desidera determinare:
1. la massima potenza totale 𝑃 dissipabile in calore da parte del circuito;
2. la carica 𝑄 ai capi del condensatore, nelle condizioni della domanda precedente.
Si osserva preliminarmente che, anche senza fare il calcolo esatto della costante
di tempo 𝜏 del circuito si può stimare il suo ordine di grandezza dai valori dei
componenti: essa sarà il prodotto della capacità, per una combinazione dei valori
delle tre resistenze, che sono dell’ordine della decina di ohm. Precisamente,
applicando il teorema del generatore equivalente, risulta che
𝜏 = 𝐶[𝑅3 ∥ (𝑅1 + 𝑅2 )] = 𝐶
(𝑅1 + 𝑅2 )𝑅3
= 2.5 𝜇𝑠 .
𝑅1 + 𝑅2 + 𝑅3
La costante di tempo risulta, pertanto, dell’ordine dei microsecondi e quindi il
calore che viene dissipato dai resistori durante il transitorio iniziale è
trascurabile, rispetto a quello che la rete assorbirà a regime. Per il computo della
potenza massima dissipabile nel circuito, allora, si può considerare il regime
stazionario corrispondente al condensatore carico.
1. In condizioni stazionarie, le tre resistenze sono collegate in serie e sono
attraversate quindi dalla stessa corrente. La massima corrente 𝐼𝑚𝑎𝑥 che le può
attraversare deve essere compatibile con la potenza massima dissipabile su
ciascuna di esse, per cui
𝐼1,𝑚𝑎𝑥 = √
𝑃𝑚𝑎𝑥
1
𝑃𝑚𝑎𝑥
1
𝑃𝑚𝑎𝑥
1
= √ , 𝐼2,𝑚𝑎𝑥 = √
= √ , 𝐼3,𝑚𝑎𝑥 = √
=√ .
𝑅1
5
𝑅2
20
𝑅3
25
da cui ricava che la massima corrente che le può attraversare vale
𝐼𝑚𝑎𝑥 = 𝐼3,𝑚𝑎𝑥 =
1
= 0.2 .
5
In definitiva, la potenza 𝑃 complessivamente assorbita dai resistori è pari a
2
2
𝑃 = (𝑅1 + 𝑅2 + 𝑅3 )𝐼𝑚𝑎𝑥
=2.
2. Il condensatore è in parallelo con il resistore 𝑅3 . Nelle condizioni di massima
corrente, la tensione ai capi del condensatore vale
𝑉 = 𝑅3 𝐼𝑚𝑎𝑥 = 5 .
Segue che la carica 𝑄 presente ai capi del condensatore è
𝑄 = 𝐶𝑉 = 1 𝜇𝐶 .
3