Altri problemi-ppt

Problema n. 1
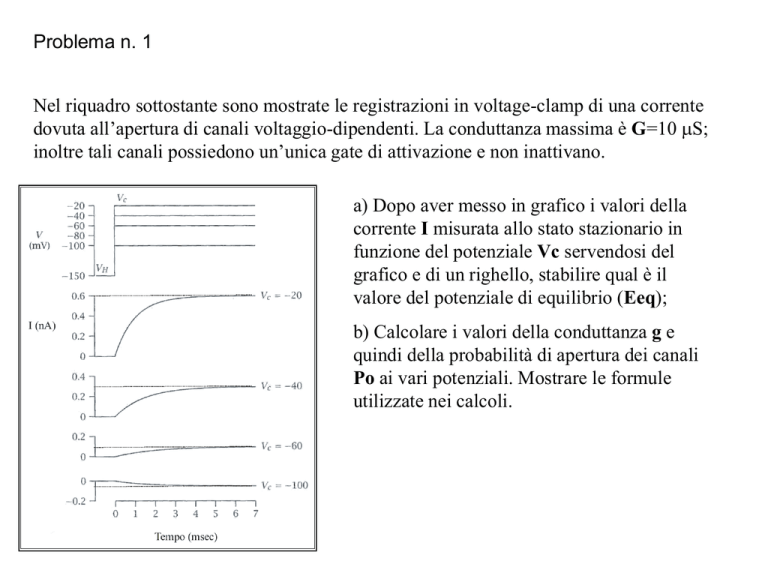
Nel riquadro sottostante sono mostrate le registrazioni in voltage-clamp di una corrente
dovuta all’apertura di canali voltaggio-dipendenti. La conduttanza massima è G=10 mS;
inoltre tali canali possiedono un’unica gate di attivazione e non inattivano.
a) Dopo aver messo in grafico i valori della
corrente I misurata allo stato stazionario in
funzione del potenziale Vc servendosi del
grafico e di un righello, stabilire qual è il
valore del potenziale di equilibrio (Eeq);
b) Calcolare i valori della conduttanza g e
quindi della probabilità di apertura dei canali
Po ai vari potenziali. Mostrare le formule
utilizzate nei calcoli.
Vc (mV)
-20
-40
-60
-80
-100
I (nA)
0.6
0.3
0.08
-0.05
g (mS)
0.01
0.0075
0.004
0.0025
Po
0.001
0.00075
0.0004
0.00025
Eeq: valore di Vm al quale la
corrente ionica a canale aperto
è zero
g=I/(Vm-Eeq)
Po=g/Gmax)
0.7
0.012
0.5
0.01
0.4
0.008
g (microS)
0.6
0.3
0.006
0.004
0.2
0.002
0.1
0
0
-120
-100
-80
-60
-40
-20
-120
0
-100
-80
-60
-40
-20
0
V (mV)
-0.1
I
0.6  10 9 A
0.6
6
6
g(20mV ) 



10
S

0
.
01

10
S  0.01mS
3
V  E (20  80 )  10 V 60
Problema n. 2
Una cellula contiene 105 canali al Ca2+ voltaggio-dipendenti, ciascuno di essi è dotato di
due gates m per l’attivazione identiche e indipendenti che seguono lo schema cinetico a
due stati sotto indicato con costanti di velocità voltaggio-dipendenti.
Gate m chiusa
a(V)
Gate m aperta
b(V)
a (V )  40e V / 20mV (sec-1)
b (V )  400e V / 40mV (sec-1)
Che ampiezza raggiungono le correnti totali di whole-cell allo stato stazionario quando la
cellula è clampata a -80 mV e a +20 mV assumendo che la cellula abbia solo canali al
Ca2+, che la conduttanza di singolo canale sia g= 20 pS e che ECa= +80 mV?
Se la probabilità di apertura della singola gate a +20 mV segue il seguente andamento
temporale: m(t) = 0.3∙(1-e-t/tau), stabilire dopo quanti ms (approssimare alla 2a cifra
decimale) la singola gate m avrà una probabilità del 50 % di essere aperta a +20 mV.
Vc
I_Ca (pA)
alfa(V)
beta(V)
m_inf
g (pS)
N
E_Ca (mV)
-80
-0.02
0.73
2956
0.0002
20
100000
80
+20
-11493
109
243
0.3096
20
100000
80
taum=1/(ab)=2.8 ms  P(0.5) → 1.94 ms
N=105
m=0.3096 (+20 mV)
g=20pS
V=+20mV; E=+80mV
I  N  m2  g ( V  E )  105 ( 0.31)2  20  1012 ( 20  80 ) 103 A
 0.0958  20 ( 60 ) 1010 A
 114.96  1010 A  11496pA
m( 20mV ) 
1
1

sec  0.0028 sec  2.8ms
a  b 109  243
taum=1/(ab)=2.8 ms  P(0.5) → 1.94 ms
P∞(+20mV)=0.3  50% di 0.3=0.15 → 0.15=0.3(1-exp(-t/2.8)) → t=2.8ln(2)=1.94 ms
Problema n. 3
Si supponga che depolarizzando in condizioni di voltage-clamp la membrana di un neurone
dal potenziale di riposo ad un certo potenziale Vf = -20 mV, la probabilita’ di apertura di una
singola gate di attivazione “n” di un canale voltaggio-dipendente raggiunga il seguente
valore allo stato stazionario: n∞(-20) = 0.5.
a) Sapendo inoltre che la conduttanza massima e’ Gmax = 10 nS, che il potenziale di
equilibrio dello ione permeante è Eeq = -70 mV e che il canale possiede due gates di
attivazione uguali e indipendenti e nessuna gate di inattivazione, calcolare il valore allo stato
stazionario della corrente I a -20 mV.
b) Se la probabilità di apertura della singola gate a -20 mV segue il seguente andamento
temporale:
n(t) = 0.5∙(1-e-t/2),
stabilire dopo quanti ms (approssimare alla 1° cifra decimale) metà dei canali apribili a -20
mV saranno aperti.
a)
Vf =
-20
mV
Eeq =
-70
n∞(-20) =
0.5
Gmax =
10
gates =
2
mV
nS
g(-20) [nS]
I(-20) [pA]
2.5
125
I=n2·Gmax(Vm-Eeq)
b)
t
n
n2
0
0.00
0.00
1
0.20
0.04
0. 60
0. 50
2
0.32
0.10
3
0.39
0.15
4
0.43
0.19
5
0.46
0.21
6
0.48
0.23
7
0.48
0.24
8
0.49
0.24
9
0.49
0.24
10
0.50
0.25
11
0.50
0.25
12
0.50
0.25
n(t) =
P(t)=n2(t)
=
0.5*(1-exp(-t/2)
(0.5*(1-exp(-t/2))2
0. 40
0. 30
0. 20
0. 10
0. 00
0
1
2
3
4
5
6
7
8
9
10
11
12
P∞=(0.5)2 = 0.25  P1/2 = (0.5)2/2 = 0.125
P1/2 = 0.125 = (0.5*(1-exp(-t/2))2
√(0.125) = 0.5*(1-exp(-t/2)
t=-2ln(0.29)=2.45 ms
13
n(t)=prob. singola gate aperta
n( t )  0.5 ( 1 et / 2 )
P(t)=prob. canale aperto = n2(t)
P( t )  n2( t )  [0.5 ( 1  e  t / 2 )]
Calcolo analitico di P∞:
Calcolo grafico di P∞:
P  lim t  n2( t )  0.52  0.25
P  0.25  P1/ 2  0.125
P1/ 2  0.125  [0.5 ( 1  e  t / 2 )]
2
Dobbiamo risolvere l’equazione rispetto a t:
0.125  [0.5 ( 1  e  t / 2 )]
0.353  0.5 ( 1 et / 2 )
1
0.353
 e t / 2
0.5
t  2  ln( 0.294 )  2.45ms
2
2
Problema N. 4
La figura sottostante è la traccia idealizzata di una corrente di singolo canale registrata
da un canale del Ca2+ voltaggio-dipendente. Il potenziale di inversione di questo
canale è circa +50 mV e il voltaggio è clampato a -10 mV.
0
pA
-2
0
20 40 60 80 100 120 140 160 180 200 ms
A) qual è la conduttanza di singolo canale aperto se la relazione I/V di singolo canale è
lineare?
B) Qual è la probabilità di apertura a -10 mV?
C) Se la traccia è rappresentativa delle tracce di corrente per un lungo periodo di
tempo, stimare i valori delle quattro costanti di velocità k+1, k-1, a e b supponendo che
il modello cinetico sia a tre stati con due stati chiusi contigui ed uno stato aperto:
C2
k+1
k-1
a
C1
b
O
Non essendo possibile in questo contesto costruire e interpolare gli istogrammi di apertura e
chiusura, per il calcolo dei tempi medi di apertura e di chiusura utilizzate le medie
aritmetiche ottenute dai valori riportati nella tabella sottostante facendo però attenzione che
esiste un’attività a bursts con due distinte tipologie di chiusure aventi durate
significativamente diverse (vedi traccia idealizzata.
TABELLA
Dur. aperture (ms)
5
2.5
5
2.5
5
7.5
5
2.5
5
10
2.5
5
2.5
2.5
2.5
5
5
2.5
Dur. chiusure (ms)
2.5
7.5
5
5
5
35
5
7.5
2.5
35
5
5
5
5
5
10
5
C2
k+1
k-1
a
C1
b
O
1) g=i/(V-E)=-2·10-12/((-10-50)·10-3)= 0.033x10-9S=33 pS
2) Po=To/(To+Tc) = 77.5/(77.5+80+70) = 0.34
MOT = 1/b = 77.5/18 = 4.3
MC1T = 1/(a+k-1) = 80/15 = 5.3
MC2T = 1/k+1 = 70/2 = 35
MOB= a/k-1 +1 = (6+4+8)/3 = 6
→ b = 0.232 ms-1
→ a = 0.024 ms-1
→ k+1 = 0.188 ms-1
→ k-1 = 0.005 ms-1
Problema N. 5
La figura sottostante mostra delle correnti di singolo canale registrate dallo stesso
canale nella stessa cellula. Il voltaggio attraverso il patch di membrana era
clampato ai potenziali indicati.
a) Ricavando i valori di corrente dalle tracce sottostanti, plottare la relazione
corrente-voltaggio di questo canale.
b) Qual è il potenziale di equilibrio della corrente ionica che fluisce attraverso
questo canale?
c) Qual è la conduttanza di questo canale?
d) Supponendo che il canale segua uno schema cinetico del tipo:
C2
k+1
k-1
a
C1
b
O
e che al potenziale di +80 mV la durata complessiva delle aperture e chiusure sia:
To=22.1 ms, Tc1=13.6 ms e Tc2=40 ms, calcolare la probabilità di apertura.
e) Sapendo inoltre che dall’analisi degli istogrammi delle aperture e chiusure a +80
mV risulta: tau_o=0.81 ms, tau_c1=1.1 ms e tau_c2=25 ms e che il numero medio
di aperture per burst è MOB=5, calcolare le quattro costanti cinetiche a +80 mV.
Vc
i (pA)
Eeq
(mV)
g (S)
80
2
8
2.8E-11
40
0.9
0
0.2
-40
-1.4
-80
-2.5
Po(+80)=To/(To+Tc)=0.29
C2
-100
k+1
k-1
-50
a
C1
2.5
2
1.5
1
0.5
0
-0.5 0
-1
-1.5
-2
-2.5
-3
b
O=1/b
O
C1=1/(a+k-1)
C2=1/k+1
MOB=1+a/k-1
50
100
MOT
MC1T
MC2T
MOB
0.81
1.10
25.00
5.00
k+1
k-1
alfa
beta
0.04
0.18
0.73
1.23
Problema N. 6
160.00
140.00
N. eventi
120.00
100.00
80.00
60.00
40.00
20.00
0.00
0
2
4
6
8
10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44
tem pi di apertura (m s)
[B]=50 m icroM
500
450
400
350
N. eventi
Un canale viene bloccato da un
farmaco B extracellularmente e
a canale aperto. Rappresentare
lo schema cinetico minimo con
cui può essere rappresentato il
processo di blocco del canale.
Da esperimenti eseguiti nella
configurazione di outside-out e
utilizzando due diverse
concentrazioni di bloccante si
sono ricavate le distribuzioni dei
tempi di apertura mostrate nelle
due figure sottostanti.
Dai grafici calcolare i valori dei
tempi medi di apertura alle due
concentrazioni e da questi i
valori delle costanti di velocità
delle transizioni dallo stato
aperto a quello chiuso e dallo
stato aperto a quello bloccato.
[B]=5 microM
180.00
300
250
200
150
100
50
0
0
1
2
3
4
5
6
7
8
tem pi di apertura (m s)
9
10
11
12
13
14
a
k +B·[B]
b
k -B
[B]=50 mM
[B]=5 mM
37% →
B
O
C
37% →

6.3 ms

2.3 ms
[B]
(mM)
O
(ms)
1/O
(ms-1)
5
6.3
0.16
50
2.3
0.43
0.50
0.45
y = 0.0061x + 0.1281
[B]
(mM)
O
(ms)
1/O
(ms-1)
5
6.3
0.16
50
2.3
0.43
b
1/tau_open (1/ms)
0.40
0.35
0.30
0.25
0.20
0.15
0.10
0.05
0.00
0
1/O=b+k+B·[B]
k B 
1/τO-β
[B]
per [B]=0 → b=0.13 ms-1
k B 
0.16-0.13
 0.006ms 1  mM1
5
10
20
30
40
[B] (m icroM)
50
60
ESERCIZI – TEORIA DEI
CIRCUITI
- Resistenze collegate in serie
- Resistenze collegate in
parallelo
- Partitore di tensione
RESISTENZE COLLEGATE IN
SERIE
R = R1+R2+R3+…..
1) In tutte le resistenze fluisce la stessa corrente
2) La somma delle tensioni ai capi di ogni resistenza è pari a quella totale
RESISTENZE COLLEGATE IN
PARALLELO
Nel caso di due
resistenze:
Nel caso di resistenze
tutte uguali:
Req = R/n
dove n è il numero di resistenze connesse in parallelo
1) La tensione ai capi di ogni resistenza è la stessa
2) La somma delle correnti è pari a quella totale che fluisce nel circuito
PARTITORE DI
TENSIONE
1) Si applica a un gruppo di resistenze IN SERIE
2) Ai capi di ciascun resistore si stabilisce una parte della tensione totale che alimenta la serie
ESEMPIO:
Dato il circuito in figura, determinare il valore di V.
V = 50* [6/(6+4)] = 30V
ESERCIZIO 1)
Trovare la resistenza equivalente del circuito in figura.
R3, R4, R5 sono connesse in parallelo:
1/R = (1/3) + (1/6) + (1/18) = 10/18 ovvero R = 1.8 W
Il circuito è ora equivalente a quattro resistenze in serie:
Req = (1+2.2+1.8+4) = 9 W
ESERCIZIO 2)
Se quattro lampadine identiche sono collegate in parallelo e la resistenza
equivalente è di 100 W, quanto vale la resistenza di ciascuna lampadina?
Poiché la resistenza equivalente di «n» resistenze uguali collegate in parallelo è data
da Req=R/n (vedi slide 2), allora:
R = Req * n = 100 * 4 =400 W
ESERCIZIO 3)
Calcolare la resistenza totale dei circuiti in figura.
Rtot = (2+4.5+1.5) W = 8 W
R = (18*6)/(18+6) = 4.5 W
Rtot = (15+7.5+5) W = 27.5 W
R = (15/2) = 7.5 W
R = (15/3) = 5 W
ESERCIZIO 4)
In un circuito le differenze di potenziale misurate ai capi di 3 resistenze collegate in serie sono
5V, 7V, 10V. Sapendo che la corrente (I) che fluisce nel circuito vale 2A, determinare:
la tensione totale fornita al circuito, la resistenza totale, i valori delle tre resistenze.
Le tre resistenze sono collegate in serie quindi sono percorse dalla stessa corrente.
Ricaviamo i valori delle resistenze dalla legge di Ohm: R = V/I
R1 = V1/I = (5/2) = 2.5 W
R2 = V2/I = (7/2) = 3.5 W
R1 = V3/I = (10/2) = 5 W
La resistenza totale del circuito è data dalla somma delle resistenze:
Rtot = R1 + R2 + R3 = (2.5 + 3.5 + 5) W = 11 W
La tensione totale : V = IRtot = (2*11)V = 22 V
ESERCIZIO 5)
Nel circuito in figura determinare la tensione ai capi della resistenza R3. Se la resistenza
totale del circuito è pari a 100 W, determinare la corrente che fluisce attraverso il resistore
R1 e il valore della resistenza R2.
Essendo le resistenze collegate in serie, la somma delle cadute di tensione ai capi di ciascuna
resistenza deve dare il valore totale di tensione (25V), quindi:
V3 = (25-10-4)V = 11 V
La corrente che fluisce nel circuito sarà la stessa che fluisce in ogni resistenza:
I=V/R = 25/100 = 0.25 A
R2 = V2/I = 4/0.25 = 16 W
ESERCIZIO 6)
Determinare la corrente che fluisce nel circuito in figura, la tensione ai capi della resistenza da
9W e la potenza dissipata dal resistore di 11W.
Le tre resistenze sono in serie, quindi la resistenza totale:
Rtot = (4+9+11) W = 24 W
La corrente che fluisce nel circuito è la stessa che fluisce in ogni resistenza, quindi anche nella
resistenza da 9 W:
I = V/R = 12/24 = 0.5 A
La tensione (V1) ai capi della resistenza di 9 W è data da:
V1 = 0.5*9 = 4.5 V
La potenza dissipata dalla resistenza di 11 W è data da:
P = RI2 = 11 * (0.5)2 = 2.75 W
ESERCIZIO 7)
Due resistenze sono connesse in serie. La corrente che fluisce nel circuito è pari a 3A. Se una
resistenza vale 2W determinare: (a) il valore dell’altra resistenza (Rx); (b) la tensione ai capi
della resistenza di 2W.
(a) Essendo le resistenze collegate in serie la resistenza totale del circuito è data da:
R = V/I = 24/3 = 8 W
La resistenza Rx vale: Rx = (8-2) W = 6 W
(b) La tensione ai capi della resistenza 2W è:
V1 = IR1 = 3*2 = 6V
Oppure usando la formula del partitore di tensione:
V1 = 24*[2/(2+6)] = 6V
ESERCIZIO 8)
Dato il circuito in figura, determinare la resistenza totale e la corrente che fluisce nella
resistenza da 3W.
Le resistenze sono collegate in parallelo, quindi:
Rtot = (3*6)/(3+6) = 18/9 = 2 W
Poiché le resistenze sono collegate in parallelo, la tensione ai capi di ogni resistenza è la
stessa, quindi la corrente che fluisce nella resistenza da 3W è data da:
I1 = V/R1 = 12/3 = 4 A
ESERCIZIO 9)
Per il circuito mostrato in figura determinare il valore di V1. Se la resistenza totale del circuito
è 36 W, determinare la corrente che fluisce nel circuito e il valore delle resistenza R1, R2 e R3.
Le tre resistenze sono collegate in serie, quindi nel circuito circola la stessa corrente:
I = V/Rtot = (18/36) = 0.5 A
La somma delle tensioni deve essere pari alla tensione totale, quindi:
V1 = [18 – (5+3)]V = 10 V
Le tre resistenze valgono rispettivamente:
R1 = V1/I = (10/0.5) = 20 W
R2 = V2/I = (5/0.5) = 10 W
R3 = V3/I = (3/0.5) = 6 W
ESERCIZIO 10)
Dato il circuito in figura, calcolare la corrente che fluisce nella resistenza da 30 W
e stabilire quale resistenza addizionale (Rx) bisogna inserire in parallelo con le
due resistenze da 20 e 30 W affinché la corrente che fluisce nel circuito sia pario
a 8A (supponendo che la tensione resti costante).
Req= (20*30)/(20+30) = 12 W
Il circuito si riduce a due resistenze in
serie (4W e 12W). La tensione ai capi di
Req usando la regola del partitore di
tensione è:
Veq = Vtot *[(Req/(Req + 4)] = 64*(12/16) =
48V
La corrente che fluisce nella resistenza da 30 W è:
I = Veq/R = 48/30 = 1.6 A
Inserendo una terza resistenza in parallelo a quelle di 20 e 30 W comunque non
cambierà la tensione cui verrà sottoposta:
Rx = Veq/R = 48/8 = 6 W
ESERCIZIO 11)
Tre resistori sono collegati in parallelo (20W, 20W , 30W). Quale resistore (Rx)
deve essere collegato in serie ai tre al fine di avere una resistenza totale di 10W ?
Se la potenza dissipata dal circuito è 0.36 kW, quale sarà la corrente che circola
nel circuito?
La resistenza equivalente dei tre resistori è:
1/Req = 1/20 + 1/20 + 1/30 = 8/60  Req = 60/8 = 7.5 W
Se la resistenza appena ottenuta è collegata in serie con una resistenza Rx al fine di
avere una resistenza totale di 10 W, allora :
Rx = (10 – 7.5) W  2.5 W
Essendo P = RI2 allora:
I = √ (P/R) = √ (360/10) = 6A
-Condensatori collegati in serie
-Condensatori collegati in parallelo
-Carica/scarica del condensatore
CONDENSATORI
La capacità è data da: C = Q/V [capacità = carica/tensione]
La carica immagazzinata da un condensatore è data da: Q = I*t [carica =
corrente*tempo]
CONDENSATORI IN
I SERIE
condensatori in serie presentano sulle armature la stessa carica.
1/Ceq = 1/C1 + 1/C2 + 1/C3 + ….
Nel caso di due condensatori:
Ceq = (C1*C2)/(C1+C2)
Nel caso di n condensatori uguali: Ceq = C/n
CONDENSATORI IN PARALLELO
I condensatori in parallelo sono sottoposti alla stessa tensione.
Ceq = C1 + C2 + C3 + ….
ESERCIZIO 1)
a) Determinare la tensione ai capi di un condensatore di 4 mF quando è caricato con 5 mC.
b) Trovare la carica accumulata su un condensatore di capacità pari a 50 pF quando si applica
una tensione di 2KV.
a) C = 4 mF = 4*10-6 F
Q = 5 mC = 5*10-3 C
V = Q/C = (5*10-3)/(4*10-6) = (5*103)/4 = 1250 V = 1.25 KV
b) C = 50 pF = 50*10-12 F
V = 2KV = 2000 V
Q =C*V = (50*10-12 )* 2*103 = 10*10-8 = 0.1 mC
ESERCIZIO 2)
Dati due condensatori di 2 e 6 mF collegati in serie e parallelo, calcolare la
capacità equivalente in entrambi i casi.
a) Collegamento in serie: Ceq = (2*6)/(2+6) = 12/8 = 1.5 mF
b) Collegamento in parallelo: Ceq = 2+6 = 8 mF
ESERCIZIO 3)
Una corrente di 4A fluisce in un condensatore di 20 mF per 3 ms. Determinare la tensione ai
capi del condensatore.
Essendo Q =I*t = 4*3* 10-3 = 12*10-3 C
V = Q/C = (12*10-3)/(20*10-6) = 600 V
ESERCIZIO 4)
Un condensatore di 5 mF è caricato in modo che la tensione ai suoi capi sia di 800 V.
Calcolare per quanto tempo il condensatore fornirà una scarica media di corrente di 2 mA.
Q = C*V =( 5*10-6)*800 = 4*10-3 C
t = Q/I = (4*10-3 )/(2*10-3) s = 2 s
ESERCIZIO 5)
Quale condensatore deve essere collegato in serie con un condensatore di 30 mF
affinché la capacità equivalente sia di 12 mF?
Deve valere: (C1*Cx)/(C1+Cx) = Ceq
quindi:
Cx = (C1*Ceq)/(C1-Ceq) = (12*30)/(30-12) = 360/18 = 20 mF
ESERCIZIO 6)
Quattro condensatori di 1mF, 3mF, 5mF, 6mF sono collegati in parallelo ad un
generatore di tensione di 100 V. Determinare: a) la capacità equivalente del
circuito; b) la carica totale; c) la carica di ogni condensatore.
a) Ceq = (1+3+5+6) mF = 15 mF
b) Q = C*V = 15*10-6*100 = 1.5 mC
c) La carica del condensatore da 1mF : Q1 = C1*V = 1*10-6*100 = 0.1 mC
ecc……
ESERCIZIO 7)
Tre condensatori sono collegati in serie come in figura. Calcolare a) la capacità
equivalente; b) la carica di ogni condensatore e c) la tensione ai capi di ciascun
condensatore.
a) 1/Ceq = (1/3) + (1/6) + (1/12) = 7/12
da cui Ceq = 12/7 = 1.7 mF
b) Q = C*V = (1.7*10-6) * 350 = 0.6 mC
c) Essendo collegati in serie tutti i condensatori sono sottoposti alla stessa carica:
V1 = Q/C1 = (0.6*10-3)/(3*10-6) = 200 V
ecc…
PROCESSO DI CARICA di un condensatore
Alla fine del processo di carica fra le due
armature verrà riprodotta la stessa forza
elettromotrice della batteria, quindi Q = fC
(equivalente alla classica dicitura Q=VC) .
La costante  = RC rappresenta il tempo che occorre
alla carica Q(t) per raggiungere il 63% del valore
massimo (fC), ovvero:
Q(t) = 0.632*fC
PROCESSO DI SCARICA di un condensatore
La costante  = RC rappresenta il tempo che occorre
alla carica sul condensatore per scendere al 37% del
valore iniziale Q0, ovvero:
Q(t) = 0.37*Q0
ESERCIZIO 1)
Si calcoli la costante di tempo di un circuito RC in cui C=100 mF e R = 220 KW ed il tempo che
esso impiega a caricarsi fino al 50% della differenza di potenziale massima (f) fornita dalla
batteria.
= RC = (200*103)*(100*10-6) s = 22 s
Posto Q(t) = f*C*(1-e-t/RC) pari al 50% del suo valore massimo:
f*C*(1-e-t/RC) = 0.5*f*C  e-t/RC = 0.5
t = -RC ln(0.5) = -22*(-0.693) s = 15.2 s
Per la proprietà dei logaritmi:
e-A/B = C  ln(e-A/B) = ln C  -A/B = ln C  A = -B *(ln C)
ESERCIZIO 2)
Si consideri un dispositivo come in figura in cui R1 = 150 kW, R2 = 250 KW, C=200 mF collegato
ad una batteria che fornisce una forza elettromotrice (f) di 4.5 V. Una volta chiuso
l’interruttore, calcolare la costante di tempo del processo, il valore massimo di carica sul
condensatore ed il tempo affinché sulle armature si depositi il 75% di questo massimo.
Il dispositivo si comporta come un circuito RC in serie, per cui possiamo scrivere:
Req = R1 + R2 = (150+250) KW = 400 KW
Il valore massimo di carica sarà dato da: Q(max) = f*C = (4.5*200*10-6) C = 900 mC
La costante di tempo vale:
t = RC = ReqC = (400*103)*(200*10-6) = 80 s
Imponiamo che Q(t) = f*C*(1-e-t/RC) sia pari al 75% del valore massimo f*C:
f*C*(1-e-t/RC) = 0.75*f*C  e-t/RC= 0.25
T = -RC ln(0.25) = -80*(-1.39) s = 111 s
ESERCIZIO 3)
Nel grafico è rappresentato l’andamento della corrente (resistiva) in funzione del tempo
durante il processo di scarica di un circuito RC alimentato da una batteria la cui forza
elettromotrice f=9V. Si calcolino i valori della resistenza, della capacità del condensatore e
della corrente I1 (resistiva) quando t=.
It
-
- -
Ir
I
+
+ +
Esaminando il grafico, ricaviamo immediatamente la costante di tempo:
 = RC = 2s
Inoltre (confronta slide 21):
I0 = f/R = 0.0300 A
da qui ricaviamo R:
R = f/I0 = 9/0.03 = 300 W
C = /R = 2/(300) = 0.0067 F
La corrente (resistiva) I1 quando t=, è:
I1 = 0.37*(f/R) = 0.37*0.0300 = 0.0111 A
Ic
ESERCIZIO 4)
Un circuito consiste di un resistore collegato in serie con un condensatore di 0.5 mF ed ha
una costante di tempo di 12 ms. Determinare il valore del resistore e la tensione ai capi del
condensatore 7 ms dopo averlo collegato ad una batteria di 10V.
Ricaviamo R dalla costante di tempo:
R = /C = (12*10-3)/(0.5*10-6) = 24 kW
sappiamo che durante il processo di carica la tensione varia come V(t)=f*(1-e-t/).
Occupiamoci dapprima della parte esponenziale:
-t/ = -(7*10-3)/(12*10-3) = -0.583
Quindi:
V= 10*(1-e-0.583) = 10*(1-0.558) = 4.42 V
ESERCIZIO 5)
Un condensatore di 20 mF è collegato in serie con un resistore di 50 kW e a sua volta il
circuito è collegato ad una batteria (f) di 20V. Determinare:
a) il valore iniziale della corrente (capacitiva)
b) la costante di tempo del circuito
c) Il valore della corrente (capacitiva) dopo 1 secondo (corrente capacitiva)
d) Il valore della differenza di potenziale ai capi delle armature del condensatore dopo 2
secondi (dal momento in cui inizia a caricarsi)
e) Il tempo impiegato affinché la differenza d potenziale ai capi delle armature del
condensatore sia pari a 15V (a partire dal momento in cui il condensatore incomincia a
scaricarsi).
a) Il valore iniziale della corrente (capacitiva):
I0 = V/R = f/R = 20/(50*103) = 0.4 mA
-
It
- -
I
Ir
+
++
Ic
b) La costante di tempo:  = RC
 = (50*103)*(20*10-6) = 1 s
c) La corrente (capacitiva) dopo 1 secondo:
I = I0*e-(t/) = 0.4*e-(1/1) = 0.4*0.368 = 0.147 mA (decadimento della corrente capacitiva)
d) V = f*(1-e-t/) = 20*(1-e-2/1) = 20*(1-0.135) = 20*0.865 =17.3 V
e) V = V0*e-t/t  15=20*e-t/1  et = 20/15  t = ln(20/15) = ln 1.3333 = 0.288 s
Carica del condensatore: V = f*(1-e-t/)
Scarica di un condensatore: V = V0*e-t/
25
20
15
V (Carica)
V (scarica)
10
5
0
0.00
1.00
2.00
3.00
4.00
5.00
6.00
ESERCIZIO 6)
Un condensatore di 0.1 mF è caricato a 200V prima di essere collegato ad un
resistore di 4KW. Determinare:
a) la corrente iniziale di scarica
b) la costante di tempo
c) Il tempo minimo richiesto affinché la differenza di potenziale ai capi del
condensatore scenda sotto l’1%, espresso in unità di costante di tempo.
a) La corrente iniziale è data da:
I = V/R = 200/(4*103) = 0.05 A = 50 mA
b) La costante di tempo è data da:
t = RC = (4*103 ) * (0.1*10-6) = 0.0004 s = 0.4 ms
c) L’1% del valore iniziale di differenza di potenziale corrisponde a 2V. Quindi:
V=V0*e-t/t
 2 = 200 * e-t/0.4
t = -0.4ms*ln(0.01) = 1.84 ms che corrispondono a circa 5 volte la costante di
tempo 
ESERCIZIO 7)
Quando un condensatore di 3 mF è collegato ad un resistore la differenza di potenziale decade
del 70% in 3.9s. Determinare il valore del resistore.
Detto V0 il valore iniziale della differenza di potenziale e V quello finale, allora se decade del 70%
significa che dopo 3.9s V corrisponde al 30% di V0, ovvero:
V/V0 = 30/100 = 0.3
Quindi: V = V0*e-t/t  V/V0 = e-t/
0.3 = e-3.9/ da cui ricavo :
ln (0.3) -3.9/

 = -3.9/ln(0.3) = 3.25 s
Possiamo ora calcolare R:
R = /C = 3.25/(3*10-6) = 1.08*106 W = 1.08 MW
ESERCIZIO 8)
Durante un potenziale d’azione il potenziale di membrana Vm di una cellula passa
transitoriamente da -70 mV a +30 mV. Quando il neurone si trova a +30 mV, quale è la
variazione di carica accumulata sulla faccia interna della membrana somatica? Quanti ioni
hanno prodotto questo spostamento di carica? [Considerare la capacità della cellula dell’esercizio
precedente].
La variazione del potenziale di membrana è: [+30-(-70)]mV = 100 mV.
La carica spostata sulla superficie di membrana è:
Q = C*V = 0.79 pF * (100*10-3 V) = 79*10-15 C
Poiché durante la fase iniziale del potenziale d’azione la depolarizzazione della membrana è
dovuta all’influsso di ioni sodio (monovalenti), sulla faccia interna della membrana si sono
accumulati:
79*10-15 / 1.6*10-19 = 493750 ioni monovalenti
Leggi di Kirchhoff
ESERCIZIO 1)
Determinare le correnti che fluiscono in ogni ramo del circuito in figura.
Dopo aver deciso il verso della corrente per ogni maglia, applichiamo le leggi di Kirchhoff:
-E1 + R1I1 –E2 + R2I2 = 0
E2 - R2I2 + R3I3 = 0
I1 = I2 + I3

2.5*(6 + 2.5I3) + 0.5 I3 = 16
I2 = 6 + 2.5I3

I1 = I2 + I3
-4 + 0.5I1 –12 + 2I2 = 0
12 - 2I2 + 5I3 = 0
I1 = I2 + I3
I1 = 6.52 A
I2 = 6.37 A
I3 = 0.15 A
 ……
ESERCIZIO 2)
Si calcoli il valore della corrente in ciascuno dei rami del circuito in figura e la tensione fra i
due nodi, sapendo che:
f1 = 12 V
f2 = 15 V
R1 = 100 W
R2 = 200 W
R3 = 300 W
Servono 3 equazioni per determinare il valore
delle correnti incognite.
I1 = I2 + I3 (equazione per le correnti)
-f1 +R1I1 +R2I2 = 0
-f2 + I3R3 + R2I2 = 0
(equazioni per le cadute di potenziale)
Risolvendo il sistema, dopo alcuni passaggi otteniamo:
I3 = (R2I2-f2)/R3
f1 = R1I2 +R2I2 + R1(R2I2-f2)/R3
I1 = 27.3 mA
I2 = 46.4 mA
VA – VB = R2I2 = (200*0.046)V = 9.2 V
I3 = -19.1 mA
ESERCIZIO 3)
Scrivere senza risolverle le tre equazioni che permettono di ricavare il valori delle correnti in
ogni ramo del circuito, supponendo noti i valori delle resistenze e delle batterie.
Scelto il verso della corrente (frecce blu) possiamo scrivere le tre equazioni:
-f1 + R1I1 – f2 + R2I2 = 0
f2 + f3 – R3I3 =0
I1 = I2+I3
ESERCIZIO 4)
Scrivere senza risolverle le tre equazioni che permettono di ricavare il valori delle correnti in
ogni ramo del circuito, supponendo noti i valori delle resistenze e delle batterie.
R1
f2
R3
R2
f1
Scelto il verso della corrente (frecce nere) possiamo scrivere le tre equazioni:
-f1 + R1I1 – f2 + R2I2 = 0
f2 + R2I2 + R3I3 =0
I1 = I2+I3