La divisione e l`1

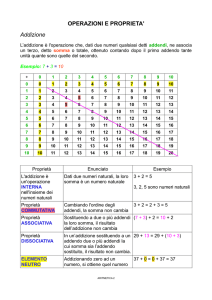
Consideriamo due numeri naturali, per
esempio 4 e 7. Contando successivamente,
dopo le unità del primo, le unità del secondo si
esegue l’operazione aritmetica detta addizione,
il cui simbolo è “+”;
4 + 7 = 11
Possiamo quindi dire che:
L’addizione è l’operazione aritmetica che ci permette di associare a due
numeri, detti addendi, un terzo numero, detto somma, a cui si perviene
contando successivamente al primo tanti numeri consecutivi quante sono
le unità del secondo.
Le parole della matematica:
4 + 7 = 11
addendi
somma
L’addizione è un’operazione interna all’insieme dei
numeri naturali N, ovvero l’insieme dei numeri
naturali è chiuso rispetto all’addizione.
• Proprietà commutativa
21 + 7 + 10 = 38
7 + 21 + 10 = 38
•Proprietà associativa
22 + 8 + 5 = 35
30
+ 5 = 35
• Proprietà dissociativa
27 + 32 = 59
20 + 7 + 30 + 2 = 59
Possiamo riassumere dicendo che:
Per la proprietà commutativa la somma di due o più addendi non
cambia cambiando l’ordine degli addendi.
Per la proprietà associativa la somma di tre o più addendi non
cambia se al posto di alcuni di essi si sostituisce la loro somma.
Per la proprietà dissociativa la somma di due o più addendi non
cambia se a uno o più di essi se ne sostituiscono altri la cui somma è
uguale all’addendo sostituito.
Consideriamo due numeri naturali, per esempio 10 e 6; se alle unità del
primo numero togliamo le unità del secondo, eseguiamo l’operazione
aritmetica detta sottrazione, il cui simbolo è “-”;
10 - 6 = 4
Possiamo dire che:
La sottrazione è l’operazione che ci permette di associare a due numeri,
detti rispettivamente minuendo e sottraendo, un terzo numero, se esiste,
detto differenza o resto, che addizionato al sottraendo ci dia come
risultato il minuendo.
Le parole della matematica:
6-4=2
minuendo – sottraendo = differenza
Consideriamo un numero naturale, per
esempio 21, e addizioniamo a esso un altro
numero, per esempio 9;
21 + 9 = 30
+9
21
30
Al risultato sottraiamo ancora 9:
30 – 9 = 21 abbiamo ottenuto il numero di
partenza 21.
-9
La sottrazione è l’operazione inversa dell’addizione.
La sottrazione non è un’operazione interna all’insieme dei numeri naturali
ovvero l’insieme dei numeri naturali non è chiuso rispetto alla sottrazione.
Consideriamo le seguenti sottrazioni
6 - 10 = ?
7 - 21 = ?
Come puoi vedere, se il minuendo è minore del sottraendo non esiste un
numero naturale che ci dia tale differenza.
La sottrazione non è un’operazione interna all’insieme dei numeri naturali
ovvero l’insieme dei numeri naturali non è chiuso rispetto alla sottrazione.
La differenza fra due numeri non cambia se a entrambi si addiziona o
si sottrae uno stesso numero.
Proviamo con i numeri:
342 – 124 = 218
342 – 124 = (342 + 6) - (124 + 6) = 348 – 130 = 218
342 – 124 = (342 – 4) – (124 – 4) = 338 – 120 = 218
Consideriamo due numeri naturali, per esempio 3 e 4; sommando tanti
addendi tutti uguali al primo numero tante volte quante sono le unità del
secondo numero otteniamo l’operazione aritmetica detta moltiplicazione, il
cui simbolo è “x” o “•”;
3 x 4 = 3 + 3 + 3 + 3 = 12
Possiamo quindi dire che:
La moltiplicazione è l’operazione aritmetica che ci permette di associare a
due numeri, detti fattori, un terzo numero, detto prodotto, a cui si perviene
addizionando tanti addendi uguali al primo numero quante sono le unità del
secondo.
Le parole della matematica:
3 x 4 = 12
fattori
prodotto
Rappresentiamo sulla retta orientata la moltiplicazione:
3 x 4 = 12
+3
0
+3
3
+3
6
u
+3
9
12
La moltiplicazione è un’operazione interna all’insieme dei numeri naturali,
ovvero l’insieme dei numeri naturali è chiuso rispetto alla moltiplicazione.
Ricordiamo la procedura di calcolo
523 x 46 =
5 2 3 x
4 6 =
3 1 3 8
2 0 9 2
4 3, 2 5 x
2, 3 =
1 2 9 7 5
8 6 5 0
24 0 5 8
9 9,4 7 5
43,25 x 2,3 =
Proprietà commutativa
21 x 4 = 84
4 x 21 = 84
Proprietà associativa
Proprietà dissociativa
3 x 4 x 2 = 24
2 5 x 10 = 250
12
x 2 = 24
5 X 5 x 10 = 250
Proprietà distributiva
3 x (7 + 4) = 3 x 11 = 33
(3 x 7) + (3 x 4) = 21 + 12 = 33
Possiamo riassumere dicendo che:
Per la proprietà commutativa il prodotto di due o più fattori non cambia
cambiando l’ordine dei fattori.
Per la proprietà associativa il prodotto di tre o più fattori non cambia se al
posto di alcuni di essi si sostituisce il loro prodotto.
Per la proprietà dissociativa il prodotto di due o più fattori non cambia se a
uno o più di essi se ne sostituiscono altri il cui prodotto è uguale al fattore
sostituito.
Per la proprietà distributiva per moltiplicare un numero per una somma (o
una differenza) si può moltiplicare il numero per ciascun termine della
somma (o della differenza) e successivamente addizionare (o sottrarre) i
prodotti ottenuti.
La divisione è l’operazione aritmetica che ci permette di associare a due
numeri, detti rispettivamente dividendo e divisore (di cui il divisore è
diverso da zero), un terzo numero, se esiste, detto quoziente, che,
moltiplicato per il divisore, ci dia come risultato il dividendo.
dividendo
Le parole della matematica:
quoziente
28 : 7 = 4
divisore
Consideriamo alcune divisioni:
20 : 4 = 5
110 : 11 = 10
29 : 5 = ?
75 : 5 = 15
108 : 9 = 12
31 : 4 = ?
Come puoi notare non sempre esiste un numero naturale che sia il
quoziente fra due numeri naturali qualsiasi. Diciamo che:
La divisione non è un’operazione interna all’insieme dei numeri naturali,
ovvero l’insieme dei numeri naturali non è chiuso rispetto alla divisione.
Proprietà invariantiva
Proprietà distributiva
364:14=26
(2 5 + 1 0) : 5 = 3 5 : 5 = 7
(3 6 4 : 2) : (1 4 : 2) = 1 8 2 : 7 = 2 6
(2 5 : 5) + (1 0 : 5) = 5 + 2 = 7
(3 6 4 x 2) : (1 4 x 2) = 7 2 8 : 2 8 = 2 6
(2 4 – 1 8) : 3 = 6 : 3 = 2
(2 4 : 3) – (1 8 : 3) = 8 – 6 = 2
Possiamo riassumere dicendo che:
Per la proprietà invariantiva il quoziente fra due numeri non cambia se
entrambi si dividono o si moltiplicano per uno stesso numero, diverso da zero.
Per la proprietà distributiva per dividere una somma (o una differenza) per
un numero si può dividere ciascun termine della somma (o della differenza)
per quel numero e successivamente addizionare (o sottrarre) i quozienti
ottenuti.
Consideriamo un numero
naturale, per esempio 21,
e moltiplichiamolo per un
altro numero, per esempio
7:
x7
147
21
21x7=147
Dividiamo il risultato
ottenuto ancora per 7:
147:7=21
:7
La divisione è l’operazione inversa della moltiplicazione.
Ricordiamo le regole per eseguire rapidamente una moltiplicazione o
una divisione per 10, 100, 1000, ….
Per la moltiplicazione:
Per la divisione:
Se il numero è naturale, si aggiungono
alla sua destra tanti zeri quanti sono
quelli del 10, 100, 1000, … per cui si
moltiplica. Se il numero è decimale, si
sposta la virgola verso destra di tanti
posti quanti sono gli zeri del 10, 100,
1000, … per cui si moltiplica e, se
mancano cifre, si aggiungono zeri.
Se il dividendo è un numero naturale, si
separano con la virgola a partire da
destra tante cifre decimali quanti sono
gli zeri del 10, 100, 1000, … per cui si
divide e, se mancano cifre, si
aggiungono zeri. Se il dividendo è
decimale, si sposta la virgola verso
sinistra di tanti posti quanti sono gli zeri
del 10, 100, 1000, … per cui si divide e,
se mancano cifre, si aggiungono zeri.
35x100=3500
5,7x100=570
75:100=0,75
91,7:10=9,17
L’addizione e lo 0
0+0=0
1+0=0+1=1
7+0=0+7=7
13 + 0 = 0 + 13 = 13

Osserviamo che la somma
Diciamo che lo 0 è
di due addendi, di cui uno è
l’elemento neutro
0, è uguale all’altro
dell’addizione.
addendo; un qualsiasi
numero naturale addizionato
a 0 rimane invariato.
La sottrazione e lo 0
0–0=0
4–0=4
0–4=?
13 – 0 = 13
0 – 13 = ?

Osserviamo che se
sottraiamo lo zero a
un numero qualsiasi
il numero resta
invariato ma non vale
il viceversa.
Diciamo che lo 0 non
è elemento neutro per
la sottrazione.
La moltiplicazione e lo 0
0x0=0
1x0=0x1=0
7x0=0x7=0
25 x 0 = 0 x 25 = 0

Osserviamo che il prodotto
di due numeri, di cui almeno
uno è 0, è sempre uguale a
0. Si dice che lo zero
assorbe il risultato della
moltiplicazione.
Diciamo che lo 0 è
l’elemento
assorbente della
moltiplicazione.
La divisione e lo 0

Un po’ più complesso è
il comportamento dello
zero nella divisione;
esaminiamolo
attraverso degli esempi:
0 : 0 = 0, 1, 2, 3, ….; qualsiasi numero (indeterminata)
0 : 1 = 0 diciamo che 0 : numero qualsiasi = 0
1 : 0 = ? diciamo che un numero qualsiasi : 0 è
impossibile
L’addizione, la sottrazione e l’1
In queste due operazioni l’1 non assume comportamenti particolari.
La moltiplicazione e l’1
1x1=1
2x1=1x2=2
7x1=1x7=7

Osserviamo che il prodotto di due fattori, di
cui uno è l’unità, è sempre uguale all’altro
fattore. Cioè un qualsiasi numero moltiplicato
per 1 rimane invariato.
Diciamo che l’1 è l’elemento neutro della moltiplicazione.
La divisione e l’1
0:1=0
1:1=1
25 : 1 = 25
1:2=?
1:5=1
1 : 29 = 1


Se il numero 1 è divisore, si comporta come elemento
neutro, lascia cioè invariato il dividendo.
Se il numero 1 è dividendo, la divisione è impossibile
nell’insieme dei numeri naturali.
Quindi il numero 1 non è elemento neutro per la divisione.
La divisione e l’1
1:1=1
2:2=1
29 : 29 = 1

La divisione fra due numeri uguali dà come
quoziente 1.