Appunti di matematica
Numeri Naturali
Numeri Naturali
I numeri naturali formano un insieme infinito che si indica generalmente con N:
Ν = {0,1, 2, 3, 4, 5, 6, 7,...}
Le quattro operazioni
Addizione
Sottrazione
Moltiplicazione
Divisione
Osservazioni
§ Solo l’addizione e la moltiplicazione danno sempre come risultato un numero
naturale.
Esempi. 3 + 7 = 10 ; 3 × 7 = 21
§ Non sempre esiste il risultato in N per la sottrazione.
Esempio. 4 − 6 = ?
§ Non sempre esiste il risultato in N per la divisione.
Esempio.
Il risultato di 15:6 non esiste in N,
perché non esiste un numero naturale
m tale che m × 6 = 15 .
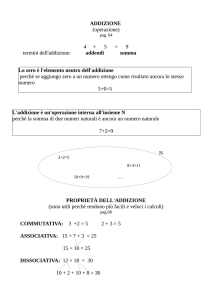
Addizione o somma
Proprietà
commutativa
associativa
Elemento neutro: “0”
Proprietà dell’addizione “+”
Espressione
a+b=b+a
(a + b) + c = a + (b + c)
a+0= 0+a = a
Esempio
3+7 =7 +3
(5 + 1) + 3 = 5 + (1 + 3)
2+0 = 0+ 2 = 2
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
Appunti di matematica
Numeri Naturali
Moltiplicazione
Proprietà
commutativa
associativa
Distributiva a destra
rispetto all’addizione
Distributiva a sinistra
rispetto all’addizione
Elemento neutro: “1”
Proprietà della moltiplicazione “x”
Espressione
a×b = b× a
( a × b ) × c = a × (b × c )
Esempio
3× 7 = 7 × 3
(5 × 1) × 3 = 5 × (1 × 3)
( a + b) × c = a × c + b × c
(5 + 1) × 3 = 5 × 3 + 1 × 3
a × (b + c ) = a × b + a × c
6 × (7 + 2 ) = 6 × 7 + 6 × 2
a × 1 = 1× a = a
3 × 1 = 1× 3 = 3
Legge di annullamento del prodotto
Se in un prodotto un fattore è zero, anche il prodotto è zero. Viceversa, se un
prodotto è zero, uno almeno dei suoi fattori è zero.
Sottrazione
Proprietà
invariantiva
Proprietà della sottrazione “-“
Espressione
a − b = (a + n ) − (b + n ) con a ≥ b
a − b = (a − n ) − (b − n ) con a ≥ b ≥ n
Esempio
12 − 7 = (12 + 3) − (7 + 3)
12 − 7 = (12 − 3) − (7 − 3)
Divisione
Proprietà
invariantiva
Distributiva a sinistra
rispetto all’addizione
Proprietà della divisione “:”
Espressione
a : b = (a × n ) : (b × n ) con b ≠ 0, n ≠ 0
a : b = (a : n ) : (b : n ) con b ≠ 0, n ≠ 0
( a + b) : c = a : c + b : c
Esempio
10 − 8 = (10 × 3) − (8 × 3)
12 : 4 = (12 : 2) : (4 : 2 )
(6 + 8) : 2 = 6 : 2 + 8 : 2
Osservazione
Non è possibile la divisione con il divisore uguale a zero.
Esempio. 6 : 0 non ha significato. Infatti non è possibile trovare un numero che
moltiplicato per 0, dia come risultato 6.
In questo caso si dice che l’operazione è impossibile.
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta