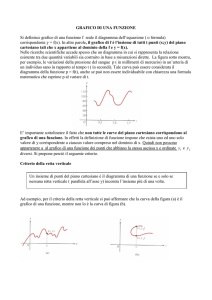
Esercizi –piano cartesiano, funzione, grafico
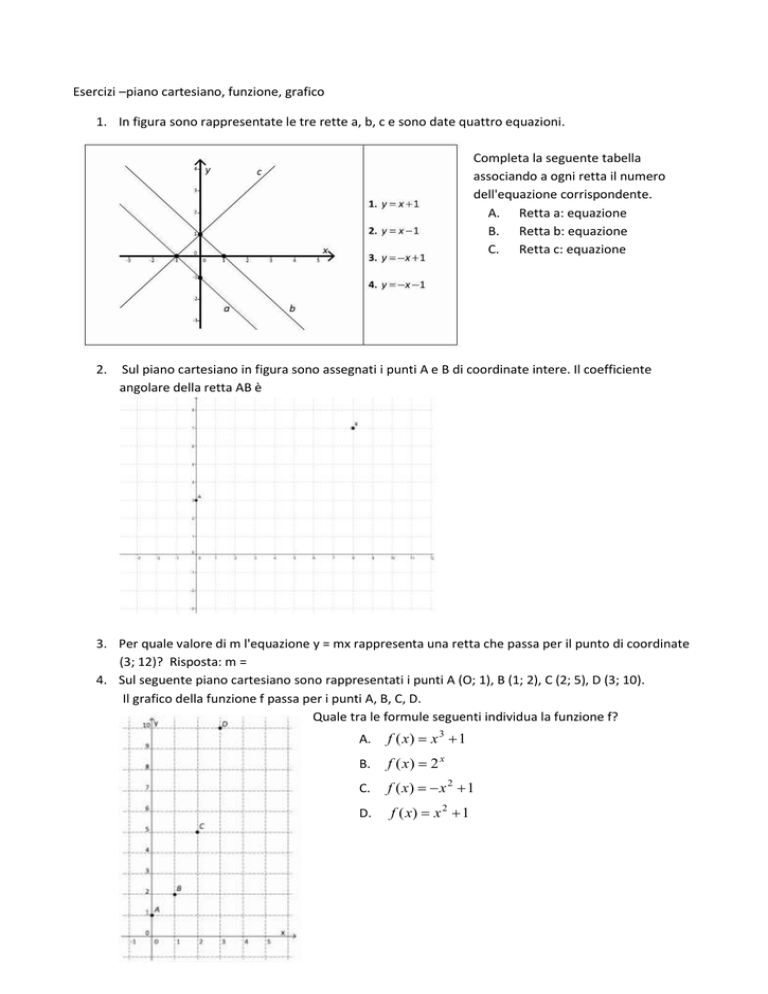
1. In figura sono rappresentate le tre rette a, b, c e sono date quattro equazioni.
Completa la seguente tabella
associando a ogni retta il numero
dell'equazione corrispondente.
A. Retta a: equazione
B. Retta b: equazione
C. Retta c: equazione
2.
Sul piano cartesiano in figura sono assegnati i punti A e B di coordinate intere. Il coefficiente
angolare della retta AB è
3. Per quale valore di m l'equazione y = mx rappresenta una retta che passa per il punto di coordinate
(3; 12)? Risposta: m =
4. Sul seguente piano cartesiano sono rappresentati i punti A (O; 1), B (1; 2), C (2; 5), D (3; 10).
Il grafico della funzione f passa per i punti A, B, C, D.
Quale tra le formule seguenti individua la funzione f?
A.
f ( x) x 3 1
B.
f ( x) 2 x
C.
f ( x) x 2 1
D.
f ( x) x 2 1
5. Uno dei seguenti grafici rappresenta la funzione definita da y = 1 – 4x nell’insieme dei numeri reali.
Quale?
A. grafico A
B. Grafico B
C. Grafico C
D. Grafico D
6. Su un piano cartesiano sono rappresentati i grafici delle funzioni f e g definite nell’insieme dei
numeri reali e rappresentate dalle formule f(x) = 2x - 5 e g(x) = - 3x + 1.
A.
A.
B.
C.
D.
f(x) = g(x) se e solo se x = 1,2
f(x) > 0 se e solo se x > 0
f(x) = 0 se e solo se x = 2,5
g(x) > f(x) se e solo se x < 1,2
7. Nel piano cartesiano Oxy la retta di equazione y 3 x 5 e la retta di equazione y
tra loro parallele; il valore di k è:
A. -3
B. -6
C. 3
D. 6
V
V
V
V
F
F
F
F
k
x 1 sono
2
8. Qual è l’area del quadrilatero ABCD rappresentato in figura?
Risposta:
cm²
9. Osserva la figura.
Se il lato di ogni quadretto della griglia corrisponde a 1 m,
allora la superficie del poligono misura
m2
10. Sul seguente piano cartesiano sono rappresentate le rette F, G, H, K.
Associa a ciascuna delle equazioni in tabella la retta corrispondente.
a. ------------------y=-2x+4 -----------b. ------------------y = -2x -------------c. ------------------y =-2 ----------------
11. Osserva la seguente figura.
Il triangolo A'B'C' è stato ottenuto dal
triangolo ABC attraverso
A. Una simmetria di centro (0;3)
B. Una rotazione antioraria di centro (0;0)
e ampiezza a 90°
C. Una simmetria assiale rispetto all’asse y
D. Una rotazione antioraria di centro (1;1)
e ampiezza a 90°
12. Una popolazione batterica aumenta nel tempo con un tasso di crescita costante
(cioè la variazione percentuale del numero di batteri tra un qualunque giorno e il
giorno precedente è costante). La tabella seguente riporta il numero N di milioni di
batteri della popolazione al trascorrere dei giorni. Quale fra i seguenti grafici può
rappresentare l’andamento del numero N di batteri al variare del tempo t, in
almeno 20 giorni?
A.
B.
Grafico1
grafico2
C.
D.
Grafico3
grafico4
13. Considera la funzione definita da: y = 3x + 1.
Quale dei seguenti grafici può rappresentare questa funzione?
Grafico 3
A.
B.
C.
D.
Grafico 1
Grafico 2
Grafico 3
Grafico 4
13a. Quale valore di y si ottiene per x = 0 ?
13b. Per quale valore di x si ottiene y = 0 ?
grafico 4
13c. Per quali valori di x la y assume valori positivi?
14. Mario va in vacanza in una località sciistica. Per usufruire degli impianti
di risalita (seggiovie, funivie, ...), può scegliere tra due offerte, A e B,
entrambe valide per tutta la stagione invernale.
Offerta A: costo iniziale fisso di 100 euro più 15 euro per ogni
giornaliero (ossia per ogni giorno in cui si usano gli impianti di risalita).
Offerta B: 30 euro per ogni giornaliero, senza costo iniziale.
Osserva la figura sotto.
14a. Il grafico F rappresenta l'offerta
(indica A oppure B)
14b. Completa la seguente tabella, relativa all’offerta B.
Numero di giorni in cui Mario usufruisce degli impianti di
risalita
1
2
3
Costo in euro
30
14c. Se Mario usa gli impianti di risalita solo per cinque giorni durante la
stagione invernale, quale offerta gli conviene scegliere?
14d. Scrivi due formule, una per l’offerta A e una per l’offerta B, che
esprimano il costo c al variare del numero di giornalieri g.
14e. Qual è il numero di giornalieri per cui il costo dell’offerta B è una volta e
mezza il costo dell’offerta A?
15. Con “spazio di frenata” intendiamo lo spazio che un’auto percorre
dall’inizio della frenata fino a quando si ferma.
Una regola pratica per stimare lo spazio di frenata (in metri), nel caso
in cui l’auto viaggi su una strada asfaltata in buone condizioni e non
bagnata, è la seguente:
“Eleva al quadrato il valore della velocità (in km/h) dell’auto all’inizio
della frenata e dividi il risultato ottenuto per 200.”
Completa la tabella seguente, che fornisce lo spazio di frenata s
(approssimato per eccesso al metro) per alcuni valori della velocità v
quando la strada si trova nelle condizioni descritte sopra.
v(km/h)
40
50
60
70
80
90
100
s(approssimato per eccesso
al metro)
8
13
--------25
------------------50
15a. Quale fra i seguenti grafici può rappresentare lo spazio di frenata s
al variare della velocità v?
A.
B.
C.
D.
Grafico1
Grafico2
Grafico3
Grafico4
16. Calcola l’area del
quadrilatero ABCD
disegnato in figura
A=
cm2
17. Di seguito sono rappresentati cinque grafici. Quale grafico è il simmetrico del grafico 1 rispetto
all’asse delle x?
A.
B.
C.
D.
grafico2
Grafico3
Grafico4
Grafico5
17a. Quale grafico è il simmetrico del grafico 1 rispetto all’asse delle y?
A. Grafico2
B. Grafico3
C. Grafico4
D. Grafico5
17b. Quale grafico è il simmetrico del grafico 1 rispetto all’origine O (0 ; 0)?
A. Grafico2
B. Grafico3
C. Grafico4
D. Grafico5
18. L’unità di misura riportata sugli assi cartesiani rappresenta 1 cm.Calcola l’area del quadrilatero
ABCD. Area=
cm2
19. Il quadrilatero A’B’C’D’ è ottenuto applicando al quadrilatero ABCD una trasformazione.
Di quale trasformazione si tratta?
A.
B.
C.
D.
Traslazione
Simmetria rispetto all’asse y
Simmetria rispetto all’asse x
Rotazione attorno all’origine