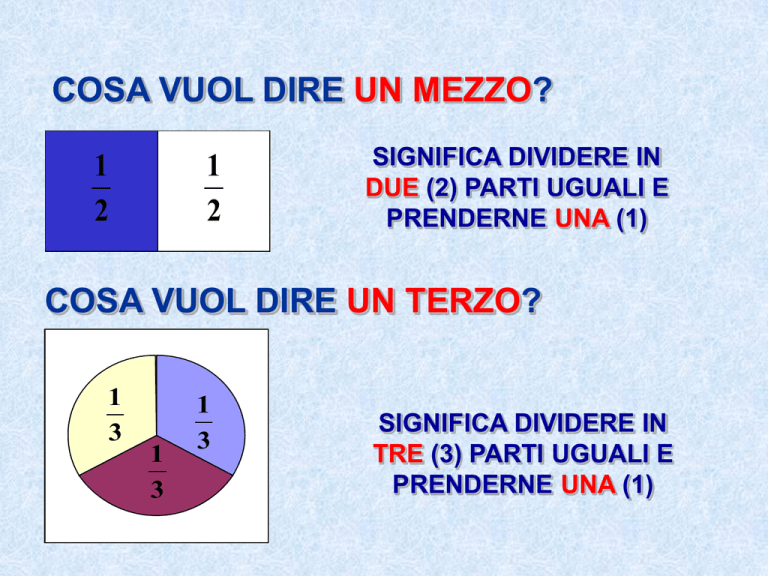
COSA VUOL DIRE UN MEZZO?
1
2
1
2
SIGNIFICA DIVIDERE IN
DUE (2) PARTI UGUALI E
PRENDERNE UNA (1)
COSA VUOL DIRE UN TERZO?
1
3
1
3
1
3
SIGNIFICA DIVIDERE IN
TRE (3) PARTI UGUALI E
PRENDERNE UNA (1)
SE INVECE DIVIDIAMO IN CINQUE (5) PARTI
UGUALI E NE PRENDIAMO QUATTRO (4)
1
5
1
5
1
5
4
5
LA PARTE COLORATA
QUATTRO QUINTI
1
5
1
5
OGNI PARTE
RAPPRESENTA
UN QUINTO
OGNI PARTE
RAPPRESENTA
UN QUARTO
1
4
1
4
1
4
1
4
LA PARTE COLORATA
RAPPRESENTA
TRE QUARTI
3
4
QUESTI NUMERI SONO DETTI OPERATORI
FRAZIONARI O SEMPLICEMENTE FRAZIONI
Frazioni
NUMERATORE
7
11
FRAZIONE
LINEA DI FRAZIONE:
divisione
DENOMINATORE
E SI LEGGE
SETTE UNDICESIMI
Unità Frazionaria
1
n
Esempi:
QUANDO IL NUMERATORE È
UNO (1) E IL DENOMINATORE
UN NUMERO NATURALE
MAGGIORE DI UNO (1), LA
FRAZIONE SI DICE UNITÀ
FRAZIONARIA
1
2
1
3
1
4
1
5
…
UNA FRAZIONE È ANCHE IL QUOZIENTE FRA DUE
NUMERI NATURALI.
QUESTO NUMERO SI CHIAMA NUMERO RAZIONALE.
1:2
0,5
1
2
1
2
5:3
1,66...
5
3
5
3
7:2
3,5
7
2
7
2
FRAZIONE PROPRIA: N<D
quantità< intero
3
4
5
12
FRAZIONE IMPROPRIA: N>D quantità> intero
15
7
7
4
FRAZIONE APPARENTE: N = multiplo di D
naturale
8
3
4
2
1
3
numero
Riduzione ai minimi termini
24:2 12:3 4
:2
:3
30 15 5
UNA FRAZIONE SI DICE RIDOTTA AI
MINIMI
TERMINI
QUANDO
IL
MASSIMO COMUN DIVISORE FRA
NUMERATORE E DENOMINATRE È
UGUALE A 1, CIOÈ NON HANNO
DIVISORI COMUNI
D(24)={1; 2; 3; 4; 6; 8; 12; 24}
D(30)={1; 2; 3; 5; 6; 10; 15; 30}
D(4)={1; 2; 4}
D(5)={1; 5}
MCD(4;5)= 1
Frazioni Equivalenti
2
3
4
6
DUE FRAZIONI SI DICONO EQUIVALENTI SE
APPLICATE AD UNA STESSA GRANDEZZA NE
RAPPRESENTANO LA STESSA PARTE
2
3
EQUIVALENTE A
4
6
Confronto di frazioni
5 7
3 3
?
DUE FRAZIONI PER POTER
ESSERE CONFRONTATE
DEVONO AVERE LO STESSO
DENOMINATORE
SI CONFRONTANO I DUE NUMERATORI
5 7
3 3
?
No perché 5
è più piccolo
(<) di 7
5 7
3 3
E SE NON HANNO LO STESSO DENOMINATORE?
5 7
3 4
?
PRIMA SI RIDUCONO AI MINIMI TERMIMI, POI SI
CALCOLA IL m.c.m DEI DENOMINATORI DELLE
FRAZIONI RIDOTTE E SI TRASFORMA CIASCUNA
FRAZIONE NELLA FRAZIONE EQUIVALENTE CHE HA
PER DENOMINATORE IL m.c.m CALCOLATO.
INFINE SI CONFRONTANO I NUMERATORI.
M(3)={3; 6; 9; 12; 15; 18; 21; 24; …}
M(4)={4; 8; 12; 16; 20; 24; …}
12:3=
4
×4
×4
12:4=
3
×3
×3
5 20 7 21
;
;
3 12 4 12
mcm(3;4)=12
20 21
12 12
SI DIVIDE IL m.c.m PER IL DENOMINATORE DELLA FRAZIONE E PER OTTENERE IL
NUOVO NUMERATORE SI MOLTIPLICA IL NUMERATORE DELLA FRAZIONE PER IL
QUOTO TROVATO
? 4
2
Altri esempi:
15 18
? 2
DEVE ESSERE
4 RIDOTTA
4
2
2
AI MINIMI
TERMINI
18
18 9
15 9
M(15)={15; 30; 45; 60; 75; 90; …}
M(9)={9; 18; 27; 36; 45; 54; 63; …}
45:15=3
mcm(15;9)=45
45:9=5
2 ×3 6 2 ×5 10
;
;
×3
×5
9
45
15 45
6
10
45 45
Operazioni con le frazioni
ADDIZIONE E SOTTRAZIONE CON LO STESSO
DENOMINATORE
2 1 2
1 3
5 5 5 5
L’ADDIZIONE DI PIÙ FRAZIONI CON
LO STESSO DENOMINATORE È UNA
FRAZIONE CHE COME
DENOMINATORE HA LO STESSO
DENOMINATORE E COME
NUMERATORE LA SOMMA DEI
NUMERATORI
LA SOTTRAZIONE DI DUE
FRAZIONI CON LO STESSO
DENOMINATORE È UNA
FRAZIONE CHE HA COME
DENOMINATORE LO STESSO
DENOMINATORE E COME
NUMERATORE LA
SOTTRAZIONE DEI
NUMERATORI
93 9
363
44 4 4 2
ADDIZIONE
DENOMINATORI DIVERSI:
TRASFORMARE LE FRAZIONI IN FRAZIONI EQUIVALENTI
CON UGUALE DENOMINATORE (mcm tra I denominatori) POI
SOMMARE I NUMERATORI
2 1 2
41
3 8 3 11
3 4
12
12
12
12
12
mcm(3;4)=12
4 1 4
2
1
18
193
3 6
6
6 62
mcm(3;6)=6
SOTTRAZIONE
DENOMINATORI DIVERSI:
TRASFORMARE LE FRAZIONI IN FRAZIONI EQUIVALENTI
CON UGUALE DENOMINATORE (mcm tra I denominatori) POI
SOTTRARRE I NUMERATORI
53
655
18
3
11 3 11
30
30
30
30
3
6 5
mcm(5;6)=30
7
3 7
5
3
635
18
17
12 10
60
6060
mcm(10;12)=60
CASI PARTICOLARI
5
3
5
3
4
1
5
12
5
1
3
4
1
4 4
44
2
1
2
1
3
2
1
3
2
1
1
3
1
3 3
33
MOLTIPLICAZIONE
54 5
4 20
37 3
7 21
21 2
1 2:2 1
:2
34 3
4 12
6
AL NUMERATORE IL PRODOTTO DEI NUMERATORI E
AL DENOMINATORE IL PRODOTTO DEI DENOMINATORI
POI PER IL PRODOTTO FINA RIDURRE AI MINIMI
TERMINI
Esempi:
12
15
12
15
180
:20 9
:20
58 5
8 40
2
MEDOTO PRATICO:
SEMPLIFICARE UN NUMERATORE E UN DENOMINATORE ,
POI MOLTIPLICARE I NUMERATOI E I DENOM RIMASTI
3
3
1
2
12
153
3 9
5 8 1
2 2
DIVISIONE
5
10
5
35
315
1
12
3
12
10
12
10
12
8
1
1
4
2
510
53 1
11
12
312
10
4
28
IL QUOZIENTE DI DUE FRAZIONI, LA SECONDA DIVERSA
DA ZERO, SI TRASFORMA IN MOLTIPLICAZIONE
SCAMBIANDO IL NUMERATORE E IL DENOMINATORE
DELLA FRAZIONE DOPOIL SEGNO DI DIVISIONE.
DIVISIONE
5
10
5
35
315
1
12
3
12
10
12
10
12
8
1
1
4
2
510
53 1
11
12
312
10
4
28
IL QUOZIENTE DI DUE FRAZIONI, LA SECONDA DIVERSA
DA ZERO, SI TRASFORMA IN MOLTIPLICAZIONE
SCAMBIANDO IL NUMERATORE E IL DENOMINATORE
DELLA FRAZIONE DOPO IL SEGNO DI DIVISIONE.
POTENZA
2
2
2
2
2
2
2
8
2
3
3
3
3
3
3
3
2
3
3
3
3
LA POTENZA DI UNA FRAZIONE È UNA FRAZIONE CHE HA SIA IL
NUMERATORE CHE IL DENOMINATORE ELEVATI ALLA POTENZA
INDICATA
2 2
2
2 8
3
3
3
3
ATTENZIONE:
2
2
2
3
3 3
3
3 27










