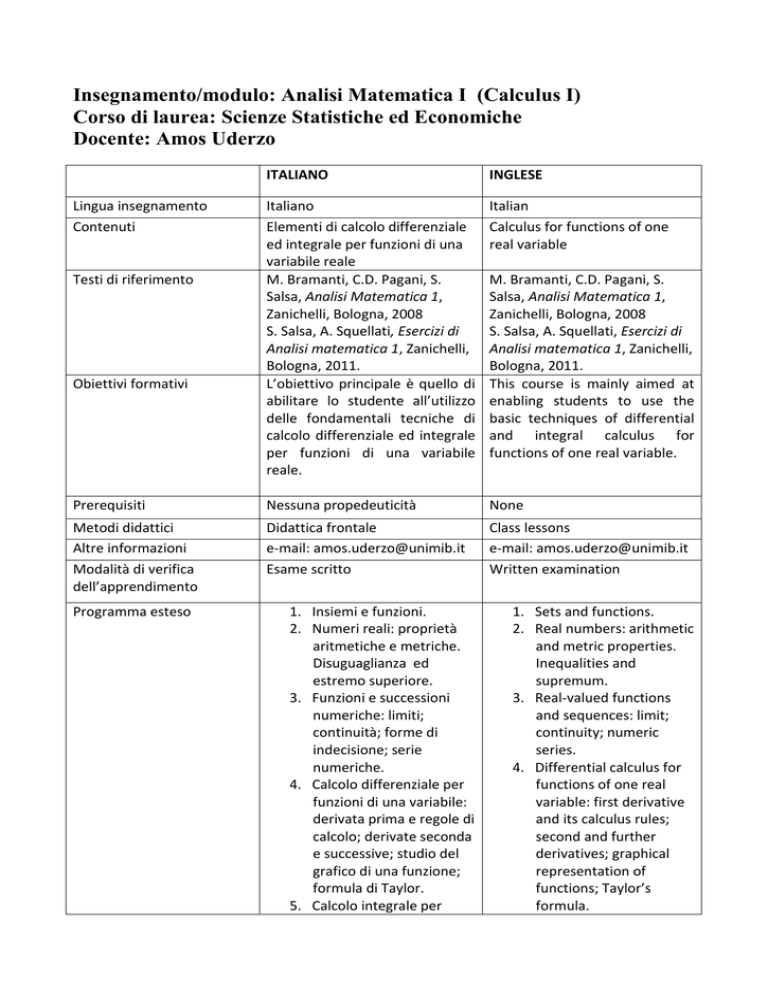
Insegnamento/modulo: Analisi Matematica I (Calculus I)
Corso di laurea: Scienze Statistiche ed Economiche
Docente: Amos Uderzo
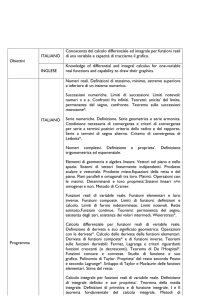
ITALIANO
INGLESE
Italiano
Elementi di calcolo differenziale
ed integrale per funzioni di una
variabile reale
M. Bramanti, C.D. Pagani, S.
Salsa, Analisi Matematica 1,
Zanichelli, Bologna, 2008
S. Salsa, A. Squellati, Esercizi di
Analisi matematica 1, Zanichelli,
Bologna, 2011.
L’obiettivo principale è quello di
abilitare lo studente all’utilizzo
delle fondamentali tecniche di
calcolo differenziale ed integrale
per funzioni di una variabile
reale.
Italian
Calculus for functions of one
real variable
Prerequisiti
Nessuna propedeuticità
None
Metodi didattici
Altre informazioni
Modalità di verifica
dell’apprendimento
Didattica frontale
e-mail: [email protected]
Esame scritto
Class lessons
e-mail: [email protected]
Written examination
Lingua insegnamento
Contenuti
Testi di riferimento
Obiettivi formativi
Programma esteso
1. Insiemi e funzioni.
2. Numeri reali: proprietà
aritmetiche e metriche.
Disuguaglianza ed
estremo superiore.
3. Funzioni e successioni
numeriche: limiti;
continuità; forme di
indecisione; serie
numeriche.
4. Calcolo differenziale per
funzioni di una variabile:
derivata prima e regole di
calcolo; derivate seconda
e successive; studio del
grafico di una funzione;
formula di Taylor.
5. Calcolo integrale per
M. Bramanti, C.D. Pagani, S.
Salsa, Analisi Matematica 1,
Zanichelli, Bologna, 2008
S. Salsa, A. Squellati, Esercizi di
Analisi matematica 1, Zanichelli,
Bologna, 2011.
This course is mainly aimed at
enabling students to use the
basic techniques of differential
and integral calculus for
functions of one real variable.
1. Sets and functions.
2. Real numbers: arithmetic
and metric properties.
Inequalities and
supremum.
3. Real-valued functions
and sequences: limit;
continuity; numeric
series.
4. Differential calculus for
functions of one real
variable: first derivative
and its calculus rules;
second and further
derivatives; graphical
representation of
functions; Taylor’s
formula.
funzioni di una variabile:
teorema fondamentale
del calcolo integrale;
metodi elementari per la
ricerca di primitive;
funzioni integrali.
6. Integrali generalizzati:
integrazione di funzioni
non limitate e/o su
intervalli illimitati.
5. Integral calculus for
functions of one real
variable: fundamental
theorem of integral
calculus; basic
integration methods;
integral functions.
6. Generalized integrals:
integration of
unbounded functions
and/or functions over
unbounded intervals.