Struttura atomica
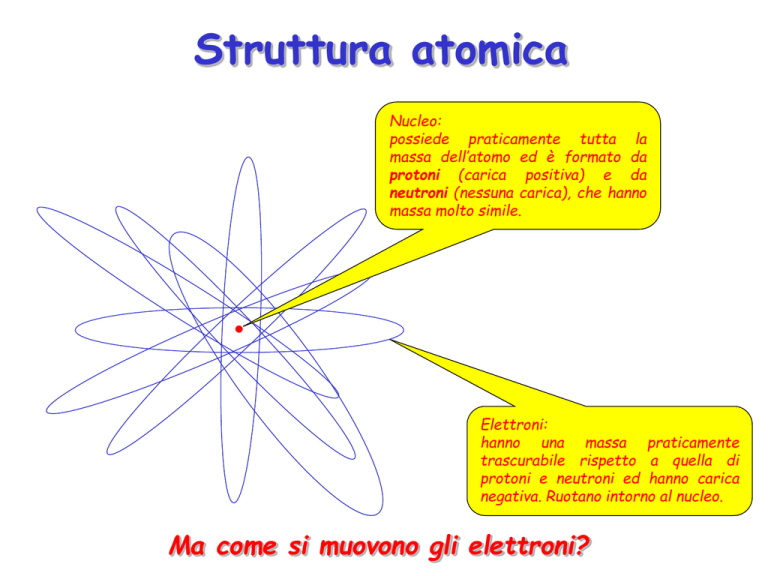
Nucleo:
possiede praticamente tutta la
massa dell’atomo ed è formato da
protoni (carica positiva) e da
neutroni (nessuna carica), che hanno
massa molto simile.
Elettroni:
hanno una massa praticamente
trascurabile rispetto a quella di
protoni e neutroni ed hanno carica
negativa. Ruotano intorno al nucleo.
Ma come si muovono gli elettroni?
Modello planetario
orbita
sole
pianeta
forza centrifuga = forza di gravitazione tra sole e pianeta
orbita
nucleo
elettrone
+
Onde elettromagnetiche
Variazione del
campo elettrico
Variazione del
campo magnetico
velocità della luce, c=
frequenza
(in hertz)
raggi gamma
raggi X
ultravioletto
lunghezza d’onda
(in centimetri)
1025
10-15
1020
10-10
1015
10-5
1010
1
105
105
1
1010
infrarosso
microonde
onde radio
luce
visibile
luce visibile
lunghezza d’onda = colore
rosso
+
blù
luce visibile
lunghezza d’onda = colore
luce bianca
Fisica classica:
Energia della luce Quadrato dell’ampiezza d’onda
(quindi indipendente dalla frequenza.)
Fisica quantistica:
Energia della luce Frequenza dell’onda
E = h
costante
di Planck
Albert Einstein
Ulm 14.3.1879 - Princeton 18.4.1955
Nobel per la Fisica 1921
Max Planck
Kiel 23.4.1858 - Gottingen 3.10.1947
Nobel per la Fisica 1918
frequenza
(in hertz)
raggi gamma
raggi X
ultravioletto
lunghezza d’onda energia
(in centimetri) h (in eV)
1025
10-15
1010
1020
10-10
105
1015
10-5
1
1010
1
10-5
105
105
10-10
1
1010
10-15
infrarosso
microonde
onde radio
luce
visibile
Spettro atomico
scarica
elettrica
in un gas
luce emessa per il
salto degli
elettroni tra le
varie orbite
spettro a righe: sono
permesse solo alcune
orbite per gli elettroni
400 nm
Idrogeno
Mercurio
Neon
500 nm
600 nm
700 nm
Modello atomico di Bohr
Modello planetario quantizzato.
Si ha orbita per un elettrone quando:
forza
attrattiva tra
nucleo ed
elettrone
momento
angolare
dell’elettrone
Niels Henrik Bohr
Copenhagen 7.10.1885 - Copenhagen 18.11.1962
Nobel per la Fisica 1922
=
=
forza centrifuga
della rotazione
dell’elettrone
intorno al nucleo
multiplo intero
della costante di
Planck
Riproduce perfettamente lo
spettro dell’atomo
d’idrogeno ... e basta.
Dualismo onda-materia
Ad ogni particella, di massa m che
si muove con velocità v, è associata
un onda di lunghezza :
h
mv
Louis Victor Duc de Broglie
Dieppe 15.8.1892 - Parigi 1987
Nobel per la Fisica 1929
elettroni
Conseguenza:
per gli elettroni in un atomo sono possibili solo
“onde stazionarie”
Oscillazione di una corda tesa
sono permesse solo le “onde stazionarie”
“onde stazionarie” su orbite circolari:
“orbita non stazionaria”
“orbita stazionaria”
Equazione di Schrödinger
Per una particella che si muove
lungo la dimensione x, con
energia E e con potenziale V(x):
2
2
h d (x )
2
V(x )(x ) E(x )
2
8 m dx
Erwin Rudolf Josef Alexander Schrödinger
Vienna 12 Agosto 1887 – Vienna 4 Gennaio 1961
Nobel per la Fisica 1933
(x ) è la funzione d’onda che
descrive la particella.
(x ) è una funzione d’onda che descrive la
particella, ma in se non ha un significato fisico, è
solo un artificio matematico.
Tuttavia:
2
(x ) P(x )
P(x) è la probabilita di trovare la particella alla
coordinata x
Principio di indeterminazione di Heisenberg
px
x
x px h
Werner Heisenberg
Würzburg 5.12.1901 - Monaco di Baviera 1976
Nobel per la Fisica 1932
L’equazione di Shrodinger è un’equazione
differenziale del second’ordine, la cui soluzione
non è un unica funzione, (x), ma una famiglia di
funzioni d’onda che si distinguono per diversi valori
di alcuni parametri (numeri quantici), n,,m(x).
Numeri quantici:
n (principale) = 1, 2, 3, …
Indica la dimensione dell’elettrone e quindi lo stato
di energia dell’elettrone
(momento angolare) = 0, 1, … (n-1)
Indica la forma dell’elettrone
m (momento magnetico) = -, …, 0, …, +
Indica l’orientamento dell’orbitale nello spazio
n = 1, 2, 3, …
= 0, 1, … (n-1)
m = -, …, 0, …, +
= 0 orbitale tipo s
= 1 orbitale tipo p
= 2 orbitale tipo d
= 3 orbitale tipo f
..
n
m
1
2
2
2
2
3
3
3
3
3
3
3
3
3
...
0 0
0 0
1 -1
1 0
1 +1
0 0
1 -1
1 0
1 +1
2 -2
2 -1
2 0
2 +1
2 +2
... ...
= 0 orbitale tipo s
1s
2s
z
= 1 orbitale tipo p
x
y
z
pz
z
x
y
px
x
y
py
Atomo con un solo elettrone (idrogeno)
4s
3s
2s
1s
4p
4d
3p
3d
2p
4f
5p
4d
5s
4p
4s
3s
3d
3p
2p
2s
1s
Atomo con un due o più elettroni
Numero quantico di spin
Una particella carica,
che ruota su stessa,
genera un campo
magnetico.
Indica il senso di
rotazione dell’elettrone
intorno al proprio asse
S
N
Un elettrone possiede un numero quantico di campo
magnetico di “spin”, che può avere solo due valori,
s = +½ e s = -½.
Ogni elettrone, in un atomo, è definito
dai suoi numeri quantici:
n = 1, 2, 3, …
= 0, 1, … (n-1)
n,,m(x)
m = -, …, 0, …, +
s = +½, -½
In un atomo non possono
esistere più elettroni con tutti
i numeri quantici uguali.
(Principio di esclusione di Pauli)
Wolfgang Pauli
Vienna 2.4.1900 – Zurigo 15.12.1958
Nobel per la Fisica 1945
E
5p
5s
4p
4s
3p
3s
2p
2s
1s
4d
3d
1 - Si “riempiono”
prima gli orbitali a più
bassa energia.
2 - Negli orbitali alla
stessa energia
(degeneri) gli elettroni
si dispongono il più
possibile con lo stesso
spin (Principio della
massima molteplicità).
E
5p
4d
5s
4p
3d
4s
3p
3s
2p
2s
1s
Ossigeno,
ha 8 elettroni.
1s2 2s2 2p4
E
5p
5s
4p
4d
3d
4s
3p
3s
2s
1s
2p
Sodio,
ha 11 elettroni.
1s2 2s2 2p6 3s1
[Ne] 3s1
Principio di Aufbau
Gli elettroni si dispongono in un atomo occupando
prima gli orbitali liberi con energia minore
Principio di esclusione di Pauli
In un atomo non possono coesistere due o più elettroni
che abbiano i quattro numeri quantici uguali
Principio di massima molteplicità
Se si dispongono orbitali degeneri (isoenergetici) gli
elettroni si distribuiscono singolarmente con spin
paralleli
H
He
Li
Be
B
C
N
O
F
Ne
Na
Mg
1s1
1s2
1s2 2s1
1s2 2s2
1s2 2s2
1s2 2s2
1s2 2s2
1s2 2s2
1s2 2s2
1s2 2s2
1s2 2s2
1s2 2s2
2p1
2p2
2p3
2p4
2p5
2p6
2p6 3s1
2p6 3s2
Al 1s2 2s2
Si 1s2 2s2
P
1s2 2s2
S
1s2 2s2
Cl 1s2 2s2
Ar 1s2 2s2
........
2p6 3s2
2p6 3s2
2p6 3s2
2p6 3s2
2p6 3s2
2p6 3s2
3p1
3p2
3p3
3p4
3p5
3p6
2
1
3
4
5
11 12
6
7
8
9
10
13 14 15 16 17 18
19 20 21 22 23
24 25 26 27 28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
55 56 57 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86
87 88 89
58 59 60 61 62 63 64 65 66 67 68 69 70 71
90 91 92 93 94 95 96 97 98 99 100 101 102 103
orbitali p
orbitali s
H
Li
orbitali d
Be
Na Mg
K
Ca Sc Ti
Rb Sr
Y
V
Cr Mn Fe Co Ni
He
B
C
N
O
F
Ne
Al Si
P
S
Cl
Ar
Cu Zn Ga Ge As Se Br Kr
Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te
Cs Ba La Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi
I
Po At Ra
Fr Ra Ac
Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu
Th Pa
orbitali f
Xe
U Np Pu Am Cm Bk Cf Es Fm Md No Lr
Ubicazione degli elettroni di valenza
He
H
Li
Be
B
K
Ca Sc Ti
Rb Sr
Y
V
N
O
F
Ne
Al Si
P
S
Cl
Ar
gruppo
Na Mg
C
periodo
Cr Mn Fe
Co Ni Cu Zn Ga Ge As Se Br Kr
Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te
Cs Ba La Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi
I
Po At Ra
Fr Ra Ac
Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu
Th Pa
Xe
U Np Pu Am Cm Bk Cf Es Fm Md No Lr
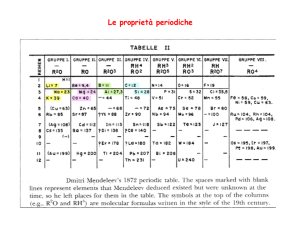
Energia di ionizzazione di un
atomo (o potenziale di
ionizzazione):
A(g) A+(g) + e-(g) H ° = I1
Affinità elettronica di un atomo:
A-(g) A(g) + e-(g)
H ° = A
Elettronegatività:
tendenza di un atomo ad attrarre
su di se gli elettroni di un legame.
Energia di
Affinità
Elettronegatività
+
ionizzazione elettronica
Elettronegatività
He
H
2,2
Li
1,0
0
Be
B
1,6
Na Mg
0,9
1,3
K
Ca
Sc
Rb
Sr
1,0
Y
1,1
Zr
Cs
Ba
La
Hf
Fr Ra
Ac
0,8
0,8
0,8
0,7
1,0
0,9
0,9
1,4
1,1
1,1
Ti
1,5
1,3
1,3
V
1,6
Cr
1,7
Nb Mo Tc
1,6
2,2
1,9
Ta
W
Re
1,5
2,4
1,9
N
O
F
Ne
2,6
3,0
3,4
4,0
Al
Si
P
S
2,6
Cl
3,2
Ar
Br
Kr
1,5
1,8
2,2
0
0
Co
Ni
Cu
Zn
Ga
Ge As
Se
Ru Rh
2,2
2,3
Pd
Ag
Cd
In
Sn Sb
Te
2,1
2,7
I
Xe
Os
Ir
Pt
Au Hg
Tl
Bi
Po
At
Rn
Mn Fe
1,6
C
2,0
1,8
2,2
1,9
2,2
1,9
2,3
2,3
1,9
1,9
2,5
1,7
1,7
2,0
1,8
1,8
2,0
2,0
2,0
Pb
2,3
2,2
2,1
2,0
2,6
2,0
3,0
2,2
0
0
0
Elettronegatività
F
4
Cl
Br
3
I
H
2
1
0
He Ne
Ar
10
20
0
30
Kr 40
50
Xe
60
70
80
Rn 90
100
110
L’energia del legame A-B è
l’energia necessaria per
provocarne la dissociazione, in
pratica è il H del processo:
AB(g) A(g) + B(g)
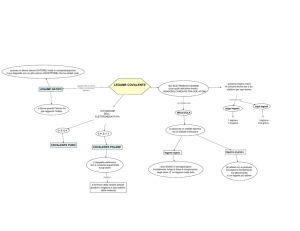
I legami chimici sono sempre
il frutto di interazioni
elettrostatiche.
“nube” elettronica con carica
negativa intorno al nucleo
nucleo con carica
positiva centrale
Le cariche negative
degli elettroni si
trovano a contatto
Se non avviene niente tra gli
Oppure, si possono verificare due
elettroni, i due atomi si respingono
casi limite:
e non si ha nessun legame.
Uno dei due atomi è più
elettronegativo dell’altro:
uno o più elettroni
passano all’atomo più
elettronegativo
Uno dei due atomi è più
elettronegativo dell’altro:
+
-
si forma uno ione positivo
ed uno negativo che si
attraggono
LEGAME IONICO
I due atomi hanno
elettronegatività paragonabile:
se si verificano le condizioni
adatte, gli elettroni possano
localizzarsi in mezzo ai due atomi
I due atomi hanno
elettronegatività paragonabile:
se si verificano le condizioni
adatte, gli elettroni possano
localizzarsi in mezzo ai due atomi
LEGAME COVALENTE
I due atomi hanno
elettronegatività diversa, ma
non troppo:
I due atomi hanno
elettronegatività diversa, ma
non troppo:
gli elettroni si localizzano in mezzo
ai due atomi, ma un po’ spostati
verso quello più elettronegativo
LEGAME COVALENTE-POLARE
Formazione di un legame ionico: KF
prima si ha il salto dell’elettrone dall’atomo K
all’atomo F
K(g) + F(g) K+(g) + F-(g)
poi si ha l’attrazione tra i due ioni di segno
opposto che si avvicineranno fino alla distanza
di legame (2,17×10-10 m)
K+(g) + F-(g) KF (g)
Bilancio energetico del un legame ionico KF
l’energia del legame K-F è il H della reazione
KF(g) K(g) + F(g)
Energia di ionizzazione:
K(g) K+(g) + e-
H = 419 kJ mol-1
Affinità elettronica:
F-(g) F(g) + e-
H = 328 kJ mol-1
Dalla legge di Coulomb:
KF(g) K+(g) + F-(g)
H = 640 kJ mol-1
(due cariche di segno opposto alla distanza di 2,17×10-10 m)
Combinando le reazioni in modo opportuno si ha:
K+(g) + e- K(g)
H = -419 kJ mol-1
F-(g) F(g) + e-
H = 328 kJ mol-1
KF(g) K+(g) + F-(g)
H = 640 kJ mol-1
KF(g) K(g) + F(g)
H = 549 kJ mol-1
In ottimo accordo con il
valore sperimentale!
Legame covalente: H2
H
H
1s1
zona di
sovrapposizione
delle due
funzioni d’onda
1s
in antifase
in fase
1s1
1s
*
orbitale
antilegante
orbitale
legante
*
orbitale antilegante
in antifase
in fase
orbitale legante
in antifase
in fase
*
orbitale
antilegante
orbitale
legante
Molecola N2:
ogni atomo N ha configurazione
elettronica 1s2 2s2 2p3
si formano un legame da un
orbitale tipo e due legami da
orbitali tipo
x
Esempio di legame covalente polare: HCl
H
Cl
1s1
… 3s2 3p5
Si forma un legame dovuto ad un orbitale
ottenuto dall’orbitale 1s di H e 3p di Cl
Distribuzione della carica degli elettroni:
H
Cl
Essendo il cloro più elettronegativo, la carica
degli elettroni tende ad addensarsi
maggiormente da quella parte.
Ne consegue che ...
+0,2
H – Cl
-0,2
La molecola è polare.
Il legame è più forte di quello che ci
si aspetterebbe se fosse covalente
Molecola H2S
H
1s1
S
1s2 2s2 2p6 3s2 3p4
1s
3p
3s
90°
1s
3p
Gli esperimenti
mostrano un
angolo di legame
di 92°
Talvolta la geometria degli orbitali atomici
non è sufficiente a spiegare la geometria
della molecola
BeH2: la struttura sperimentale è
H – Be – H
180°
BF3: la struttura sperimentale è
F
F
B
120°
F
CH4: la struttura sperimentale è a
tetraedro, con l’atomo C al centro e i
quattro atomi H ai vertici e i quattro
legami uguali a 109,5°
BeH2:
il berillio ha configurazione elettronica 1s2 2s2
2s
sp
2p
sp
al momento della formazione del legame, le due funzioni
2s e 2p danno luogo ad una combinazione lineare
formando due orbitali identici (ibridi), sp, a 180°.
CH4:
il carbonio ha configurazione elettronica 1s2 2s2 2p2
al momento della
formazione del legame,
la funzioni 2s e le tre
funzioni 2p danno
luogo ad una
combinazione lineare
formando quattro
orbitali identici
(ibridi), sp3, a 109,5°.
Ibridazione degli orbitali
s
p
sp
p
180°
s
p
sp2
p
120°
s
p
sp3
109,5°
NH3:
l’azoto ha configurazione elettronica 1s2 2s2 2p3
al momento della
formazione del legame, la
funzioni 2s e le tre
funzioni 2p danno luogo ad
una combinazione lineare
formando quattro orbitali
identici (ibridi), sp3, a
109,5°.
sp3
lone pair
H2O:
l’ossigeno ha configurazione elettronica 1s2 2s2 2p4
al momento della
formazione del legame, la
funzioni 2s e le tre
funzioni 2p danno luogo ad
una combinazione lineare
formando quattro orbitali
identici (ibridi), sp3, a
109,5°.
sp3
E
due atomi
antilegante
1 + 2
cristallo con molti atomi
banda di
conducibilità
gap di banda
legante
banda di
valenza
conduttori
isolanti
semiconduttori