IL PIANO CARTESIANO

IL PIANO CARTESIANO
Ascissa di un punto
•
•
•
•
•
•
Tra i punti di una retta e i numeri reali esiste una corrispondenza
biunivoca: cioè ad ogni punto di una retta corrisponde uno ed un solo
numero reale.
Il numero reale corrispondente ad un punto si chiama ascissa di quel
punto.
La corrispondenza si ottiene fissando un punto sulla retta (detto origine
e di solito chiamato O) ed una unità di misura (un cm, un quadretto…).
A questo punto è possibile associare i numeri relativi positivi o negativi
ponendo tante volte a destra o a sinistra dell’origine l’unità di misura.
I Numeri razionali si esprimo otto forma di intero più frazione reale
(dividendo quindi l’unità di misura tante volte quanto indicato dal
denominatore)
I numeri reali sono l’elemento separatore di 2 classi contigue di razionali
(si può semplicemente considerarli anche approssimati da un razionale)
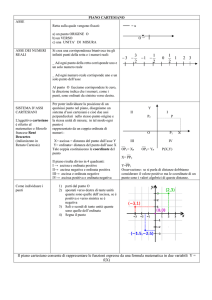
O
C=-3
-√2=-1,41
A=2
7/2=3+1/2
B=7
ascissa
Unità di misura
Distanza tra 2 punti su una retta
• Dati 2 punti A e B di ascisse xa e xb la distanza
tra A e B è
AB  xa  xb
Distanza tra 2 punti su una retta
• Dati 2 punti A e B di ascisse xa e xb la distanza
tra A e B è
AB  xa  xb
• Esempio se i punti hanno ascissa -3 e 9 la loso
distanza è
AB   3  9  6
Ascissa del punto medio su una
retta
• Dati 2 punto su una retta A e B di ascisse xa e xb
l’ascissa del punto medio è
xa  xb
xm 
2
• Esempio se i punti hanno ascissa -3 e 9 il punto
medio ha ascissa
39
xm 
3
2
Piano cartesiano
• Il piano cartesiano è suddiviso da 2 assi (asse delle
ascisse e asse delle ordinate) in 4 angoli retti chiamati
quadranti
• Partendo dall’angolo un alto a destra e seguendo il verso
antiorario sono chiamati 1°,2°,3° e 4° quadrante
y (Asse delle ordinate)
2° Quadrante
1° Quadrante
(origine)
-5 -4 -3 -2 -1
O 1
2
3
4
5
x (Asse delle ascisse)
Unità di misura
3° Quadrante
4° Quadrante
Punti del piano cartesiano
• Ogni punto del piano è individuato da una
coppia di numeri reali, detti coordinate. La prima
si chiama ascissa, la seconda ordinata.
• L’origine degli assi ha coordinate (0,0)
A (-4,3)
O (0,0)
Distanza tra punti
• La distanza tra A=(xa,ya) e B=(xb,yb) è
AB 
xb  xa    yb  ya 
2
2
Punto medio di un segmento
• Il punto medio M=(xm,ym) di un segmento AB con
A=(xa,ya) e B=(xb,yb) è
 xa  xb ya  yb 
M 
,

2 
 2
Baricentro di un triangolo
• Il baricentro di un triangolo con vertici A=(xa,ya) e
B=(xb,yb) e C=(xc,yc) è
 xa  xb  xc ya  yb  yc 
G 
,

3
3

