DS > 0

Chimica Generale e Inorganica
Processi spontanei
Un processo fisico o chimico spontaneo ha luogo
senza che venga compiuto lavoro sul sistema.
Nella direzione opposta il processo non avviene, se
non applicando energia dall’esterno.
- Passaggio di calore da un corpo caldo ad
uno freddo
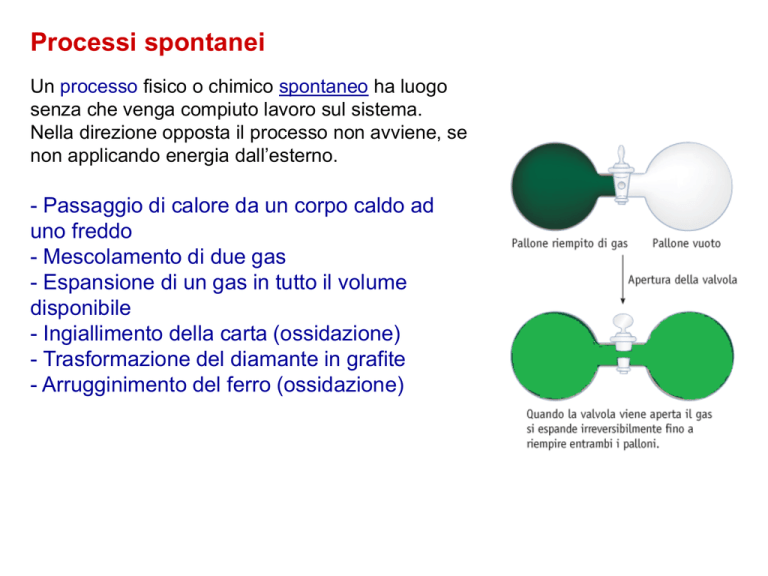
- Mescolamento di due gas
- Espansione di un gas in tutto il volume
disponibile
- Ingiallimento della carta (ossidazione)
- Trasformazione del diamante in grafite
- Arrugginimento del ferro (ossidazione)
Chimica Generale e Inorganica
CRITERI PER LA SPONTANEITA’
Per sistemi meccanici:
tendenza naturale verso una diminuzione di energia (DE < 0)
Per i sistemi chimici (con tante particelle):
la spontaneità di una trasformazione chimica è determinata dal
bilancio di DUE FATTORI:
LA DIMINUZIONE DI ENERGIA E L’AUMENTO DI “DISORDINE” !
La maggior parte delle reazioni spontanee sono esotermiche ma esistono
anche reazioni spontanee endotermiche:
H2O(s)  H2O(l) T>0°C
DHfus = +6.0 kJ/mol a
NaCl(s) Na+(aq) + Cl-(aq) DHsol = +6.4 kJ/mol
mescolamento di due gas
DHmescolamento = 0
Chimica Generale e Inorganica
•
Consideriamo 4 molecole di gas da disporre in due recipienti collegati
macrostato
ottenuto in un
solo modo:
1 microstato
macrostato
ottenuto in 4
modi diversi:
4 microstati
macrostato avente la
massima MOLTEPLICITÀ DI MICROSTATI
(6 microstati) = stato più probabile !
Espansione di un gas nel vuoto:
1 solo microstato
Estremamente
improbabile!
Chimica Generale e Inorganica
N microstati
Estremamente
probabile!
Un gas si espande nel vuoto perche’ lo stato finale ha un maggior numero di
MICROSTATI (w) a sua disposizione.
La materia e l’energia hanno piu’ modi per essere distribuite
Un sistema non si troverà in equilibrio fino a quando potrà modificare il
suo stato verso condizioni di maggior disordine.
Come possiamo misurare il DISORDINE?
Chimica Generale e Inorganica
DEFINIZIONE STATISTICA (microscopica) DELL’ENTROPIA
• Boltzmann (ca. 1900) definì la grandezza,
entropia (S), che misura il grado di disordine di
un macrostato di un sistema.
S = kB ln W
W : molteplicita’ dei MICROSTATI
kB : costante di Boltzmann
R
kB 
NA
Chimica Generale e Inorganica
W
Il numero di microstati:
 è proporzionale al volume: maggiore è il volume del sistema, più possibilità
hanno le molecole di muoversi
 è proporzionale alla temperatura: all’aumentare della energia cinetica,
aumentano gli urti e di conseguenza i microstati
 è proporzionale al numero di particelle
 diminuisce con l’aumentare della pressione: perché diminuisce lo spazio a
disposizione delle molecole
Chimica Generale e Inorganica
l’entropia aumenta se
1 - una molecola si spezza in due o più molecole
2 - si forma gas (o il numero di moli di gas aumenta)
C6H12O6(s)  2 C2H5OH(l) + 2 CO2(g)
DS > 0
CS2(l)  CS2(g)
2 NH3(g) + CO2(g)  NH2CONH2(g) + H2O(l)
2 Hg(l) + O2(g)  2 HgO(s)
DS < 0
Chimica Generale e Inorganica
3 - aumenta il grado di disordine della materia:
fusione :
Solido cristallino
ordinato
evaporazione:
mescolamento:
Liquido
disordinato
Chimica Generale e Inorganica
Processi reversibili e irreversibili
Equilibrio termodinamico
le variabili di stato di un sistema rimangono
costanti nel tempo
Processo reversibile
Trasformazione condotta in maniera che le funzioni
di stato del sistema differiscono solo di una quantità
infinitesima da un istante all’altro.
espansione reversibile:
Pint = Pest + dP
Procede attraverso una successione di stati di
equilibrio.
Può essere invertita in ogni momento
Processo irreversibile
espansione irreversibile:
Pint = Pest + DP
Trasformazione condotta in maniera che le funzioni
di stato del sistema differiscono di una quantità
finita.
Non procede attraverso stati di equilibrio.
Non può essere invertita.
Chimica Generale e Inorganica
Lavoro di espansione di un gas
Il lavoro totale (W) compiuto da un gas ideale durante un’espansione isoterma da
un volume 1 (a P1) a volume 2 (a P2) è somma dei lavori infinitesimi:
V2
Wrev   Pest dV
V1
Il lavoro è diverso se l’espansione avviene reversibilmente o irreversibilmente:
A) Espansione reversibile: Pest≈ Pint
V2
Wrev  
V1
V2
Pest dV  
V1
V2
Pint dV  
V1
nRT
dV  nRT
V
V2

V1
B) Espansione irreversibile: Pest = cost
Wirrev   Pest dV Pest  dV Pest V2  V1   Pest DV
V2
V2
V1
V1
dV
V
 nRTln 2
V
V1
Chimica Generale e Inorganica
Espansione reversibile
Wrev
V2
 nRT ln
V1
Espansione irreversibile
Wirrev  P2 (V2  V1 )
Wrev > Wirr
Tra tutte le possibili trasformazioni che un sistema ha per passare da uno stato a
un altro, quella reversibile comporta il lavoro massimo (il lavoro corrisponde
all’area nel grafico PV).
Q per processi reversibili e irreversibili
DE = Qrev – Wrev
DE = Qirrev – Wirrev
Wrev – Wirrev > 0
Chimica Generale e Inorganica
E è funzione di stato: il DE è lo stesso
nelle due trasformazioni quindi:
Qrev – Qirrev = Wrev – Wirrev
Qrev – Qirrev > 0
Qrev > Qirrev
anche il calore scambiato in una trasformazione reversibile è maggiore del calore
scambiato nella stessa trasformazione compiuta irreversibilmente.
Chimica Generale e Inorganica
DEFINIZIONE TERMODINAMICA (macroscopica) DELL’ENTROPIA (S)
Qrev
DS 
T
joule / K
Valida per un processo a
T costante (isotermo)
Il calore (Q) scambiato in un processo rende più “disordinato” il sistema
verso cui fluisce (Q acquistato); questo effetto è tanto maggiore quanto
minore è la temperatura a cui avviene.
Qrev Qirrev
DS 

T
T
Disuguaglianza di Clausius
L’entropia è una funzione di stato! DS non dipende dal cammino percorso!
DS può essere calcolata solo se la trasformazione avviene reversibilmente!
Chimica Generale e Inorganica
TERZO PRINCIPIO DELLA TERMODINAMICA (teorema di Nernst)
Una sostanza pura perfettamente cristallina allo zero assoluto (0 K) ha
entropia zero
perfettamente ordinata, le particelle sono ferme non vi è
alcuna energia cinetica: un solo microstato (W = 1).
S = kB ln W
S = kB ln 1 = 0
Chimica Generale e Inorganica
Entropia assoluta
Poichè l’entropia a 0 K è zero (S0 = 0) è possibile definire l’entropia assoluta di una
sostanza ad una data temperatura:
ΔS  S T  S 0  S T  0  S T
L’entropia di una
sostanza è sempre
positiva, cresce con la
temperatura, e può
essere calcolata
misurando la quantità di
calore reversibile per
portare la sostanza da
0K a T.
Qrev
ST 
T
Calcolo di DS nelle transizioni di fase
Chimica Generale e Inorganica
In una transizione di fase lo scambio di calore avviene
1) reversibilmente (due fasi in equilibrio tra loro)
2) a temperatura costante (temperatura di transizione)
quindi possiamo calcolare la variazione di entropia:
Q rev ΔH transizione
ΔS 

T
Ttransizione
Fusione
Vaporizzazione (T, P)
Sublimazione
ΔS evap 
Es: Variazione di entropia
per la fusione di 1 mole di
acqua a 0°C, con
DHfus = 6,0 kJ/mol:
ΔS 
ΔH fus 6,0 kJ

 22 J/(mol  K )
Tfus
273 K
ΔS f us 
ΔH f us
Tf us
ΔH vap
Tvap
Chimica Generale e Inorganica
Entropia molare standard S° è il valore dell’entropia della sostanza pura nello
stato standard (1 atm e 25°C)
La variazione di entropia DS° per una reazione chimica è data da:
ΔS 0reaz 

iS 0p ro d 

iS 0reag
Es: Calcolare la variazione di entropia standard per la reazione
CaCO3(s)
S°
92.9
 CaO(s)
38.2
+
CO2(g)
213.7
J/(mol K)
ΔS 0  S 0 (C aO )  S 0 (C O 2 )  S 0 (C aC O 3 ) 
 38.2  213.7  92.9   159 J/ K
DS>0: da un solido si ottiene un gas (grado di disordine maggiore)
Chimica Generale e Inorganica
II° principio della termodinamica
In un processo reversibile l’entropia dell’universo resta costante,
in un processo irreversibile l’entropia dell’universo aumenta
La variazione di entropia di un processo è un criterio di spontaneità solo se si
considera la somma di DS del sistema e di DS dell’ambiente, cioè il DS dell’intero
universo.
DSuniv = DSsist + DSamb > 0
DSuniv = DSsist + DSamb = 0
DSuniv = DSsist + DSamb < 0
Processo irreversibile: procede
spontaneamente
Processo reversibile: il sistema è
all’equilibrio
Processo irreversibile: procede
spontaneamente in senso inverso
Tutti i processi spontanei sono irreversibili, essi avvengono con un aumento
di entropia dell’universo  L’entropia dell’universo cresce continuamente
tendendo a un massimo.
Chimica Generale e Inorganica
ENERGIA LIBERA di Gibbs (G) : funzione di stato utile per prevedere la
spontaneità di una reazione chimica, riferita solo al sistema, tiene conto di
entrambi i fattori H ed S:
DG = DH –TDS
Equazione di Gibbs-Helmotz
Il criterio di spontaneità per le reazioni chimiche a T, P costanti:
DG < 0
DG = 0
DG > 0
reazione spontanea
reazione all’equilibrio
reazione spontanea nel senso inverso
La reazione è sempre spontanea (DG < 0) se:
è esotermica DH <0 e con aumento di disordine DS > 0
Chimica Generale e Inorganica
la variazione di energia libera del sistema che compie una trasformazione
ad una certa T costante è:
Si può prevedere se una reazione è spontanea
dal segno dei due termini, energetico (DH) ed
entropico (DS).
ΔG  ΔH -TΔ S
DS
DH < 0
DS > 0
Spontanea a ogni T
DH < 0
DS < 0
Spontanea a bassa T
(T<DH/DS)
DH > 0
DS > 0
Spontanea a alta T
(T>DH/DS)
DH > 0
DS < 0
Mai spontanea
DH
Chimica Generale e Inorganica
Calcolo della temperatura di equilibrio:
ΔG  ΔH  TΔ S
All’equilibrio DG è zero:
0  ΔH  TΔ S
La temperatura alla quale il sistema è in equilibrio:
DH
Teq 
DS
Teq è la temperatura al di sopra o al disotto della quale la reazione è spontanea
Chimica Generale e Inorganica
A) Processo di fusione, evaporazione e sublimazione:
Δ G fus  Δ H fus  T Δ S fus
poichè DHfus> 0 e DSfus> 0:
- si ha DGfus< 0, cioè la fusione è spontanea, per T > Tfus
- analogamente sono spontanee evaporazione e sublimazione per T > Ttrasf
B) Processo di liquefazione, solidificazione e brinamento:
poichè DH< 0 e DS< 0:
- si ha DG<0, cioè i processi sono spontanei, per T< Ttrasf
C) Mescolamento di gas ideali:
DH=0 e DS>0 per cui: DG = -TDS < 0
È un processo sempre spontaneo a tutte le temperature.
Chimica Generale e Inorganica
Variazione di energia libera standard DG°
DG° è la variazione di energia libera quando i reagenti e prodotti sono nei
loro stati standard (1 atm, 25 °C, concentrazione 1M).
Può essere espressa con due formule:
1) in termini delle variazioni di entalpia ed entropia standard DH° e DS°
DG° = DH° – TDS°
dove:
ΔH   ΣiΔH f (prodotti) ΣiΔH f (reagenti)
ΔS   ΣiS of (prodotti) ΣiS of (reagenti)
2) In termini di energie libere di formazione:
ΔG   ΣiG f (prodotti) ΣiG f (reagenti)
Come nel caso di DHof , il DG°f di un elemento è posto pari a zero.
Attenzione! DG è fortemente dipendente dalla temperatura, e l’ espressione (2) può
essere usata solo per la temperatura a cui si riferisce (25°C).
Chimica Generale e Inorganica
Energia libera di formazione DGfo
DGof è la variazione di energia libera per la reazione in cui 1 mole di sostanza si
forma a partire dagli elementi nei loro stati standard (1 atm e a T= 25°C).
1) Può essere calcolato a partire da DH°f e DS°f
DGfo = DHof – TDSof
DH e DS variano solo lievemente con la temperatura e in intervalli di T non troppo
grandi, possiamo considerarle circa costanti.
2) Può essere ricavato direttamente dalle tabelle di dati
termodinamici
Chimica Generale e Inorganica
Esempio – Dire se la reazione di produzione di urea è spontanea a 25 °C
(noti i Df0 ):
2NH3(g) + CO2(g)  NH2CONH2(g) + H2O
DGf0 -16
-394,4
+138,8
-237,2
kJ/mol
ΔG reaz  ΣiG f (prodotti) ΣiG f (reagenti)
DG° = [+138,8 kJ/mol - 237,2 kJ/mol]prod
– [2x -16 kJ/mol - 394,4 kJ/mol]reag = + 328 kJ
a 25 °C DG° è positivo: la reazione è sfavorita, procede nel senso opposto
Chimica Generale e Inorganica
Esempio: Calcolare il DGf0 di NH3(g) a 25°C per la reazione
½ N2(g)+ 3/2 H2(g)
noti i seguenti valori:
Hf0
0
S°
191.5
0
130.6

NH3(g)
-45.9
193
kJ/mol
J/mol K
Δ H 0   45,9  [0  0]   45,9 kJ/K
Δ S 0  193  [1 / 2  191,5  3 / 2  130,6]   98.6 5 J/K
Δ G 0  Δ H 0  T D S 0   4 5 ,9 k J  2 9 8 K  (  9 8 . 6 5  1 0  3 k J /K )   1 6 ,5 k J
Quindi la reazione è termodinamicamente favorita a temperatura
ambiente.
Chimica Generale e Inorganica
Bilanciare la seguente reazione e dire in che intervallo di T è spontanea:
Fe2O3(s) + C(s)  Fe(s) + CO2(g)
DHor = + 467.9 kJ
DSor = + 560.3 J/K
2 Fe2O3(s) + 3 C(s)  4 Fe(s) + 3 CO2(g)
A 298 K: DGor = 467.9 kJ - (298K)(0.560 kJ/K) = +300.8 kJ
DG > 0 : la reazione e’ sfavorita.
Calcoliamo T per cui DGor = 0, cioè si ha l’equilibrio:
DHor – TDSor = 0
T = DHor/DSor
467.9 kJ/0.560 kJ/K = 836 K
per T > 836 K
DG° diventa < 0,
cioè la reazione diventa spontanea !
Chimica Generale e Inorganica
A 298 K, noti i seguenti dati termodinamici, la trasformazione del
carbonio da grafite in diamante è spontanea?
Hfo(kJ/mol)
Cgrafite
Cdiamante
So (J/mol K)
0
5.740
1.895
2.377
Cgrafite  Cdiamante
DGo = DHo - TDSo
DHo = 1.895 - 0 = 1.895 kJ
DSo = 2.377 – 5.740 = -3.363 J mol-1
DGo = 1.895 kJ – 298.15 K (-3.363 x 10-3 kJ mol-1) = 2.898 kJ mol-1 > 0
la reazione da grafite a diamante non è spontanea !
Chimica Generale e Inorganica