parte 2 - Dalla probabilità alla statistica

Probabilità 02 - 1 / 53
Lezione 4
Probabilità
Probabilità 02 - 2 / 53
Nella prima parte ...
La definizione
frequentista della
probabilità:
La definizione classica
della probabilità:
La definizione
assiomatica della
probabilità:
assiomi di
Kolmogoroff
P E   0
P S   1




P 
i 1
P
P
s
E  
n
E  A

Ei  


P
i 1
nE
E   Nlim
 N
Ei 
Probabilità 02 - 3 / 53
Definizione a posteriori ( o “frequentista” )
della probabilità
definizione:
La probabilità P di un evento E è il limite a cui
tende il valore della frequenza relativa fE di E
quando N tende all’infinito.
P
nE
E   Nlim
 N
Probabilità 02 - 4 / 53
Definizione a priori ( o “classica” )
della probabilità
definizione:
La probabilità P di un evento E è il rapporto fra
il numero s dei risultati favorevoli ( cioè il numero dei risultati
che determinano E ) ed il numero n dei risultati possibili
P
s
E  
n
Ciò purché i risultati siano ugualmente possibili
e si escludano mutuamente.
La probabilità P di un evento E è certamente adimensionale!
Probabilità 02 - 5 / 53
Definizione assiomatica di probabilità
Una funzione di probabilità P è una funzione di insieme che:
– ha per dominio lo spazio degli eventi A ,
– ha per codominio l’intervallo [ 0, 1 ] ,
– soddisfa i 3 assiomi di Kolmogoroff
P E   0
• P S   1
•
E  A
• se E1 , E2 , … , En , ... è una sequenza di eventi mutamente esclusivi
dello spazio degli eventi A e se l’evento unione di tali eventi appartiene
allo spazio degli eventi A, allora la probabilità dell’evento unione è pari
alla somma delle probabilità dei singoli eventi:
P





i 1

Ei  


P
i 1
Ei 
Probabilità 02 - 6 / 53
parte 2
Dalla probabilità
alla statistica
Probabilità 02 - 7 / 53
Sommario
• La probabilità:
– funzioni di probabilità
• Variabili casuali
– concetto di “variabile casuale”
• Popolazione oggetto
– grandezza caratteristica
– Introduzione ai modelli della popolazione oggetto
• funzione “di probabilità cumulativa”
• funzione “densità di probabilità
• Funzioni di probabilità per variabili casuali discrete
Probabilità 02 - 8 / 53
Funzioni di probabilità:
la necessità di un approccio
corretto e rigoroso
Probabilità 02 - 9 / 53
Applicazione degli assiomi di Kolmogoroff
Gli assiomi di Kolmogoroff ci permettono di verificare se una
funzione arbitraria può essere assunta come “funzione di
probabilità.
esempio 1:
• Supponiamo di avere un’urna contenente 5 palline di cui 2
bianche e 3 nere: , , , , .
• L’esperimento casuale consiste nella estrazione in successione
di due palline, senza reimmissione della prima pallina estratta.
• Lo spazio campione S è dato da:
S = { (,), (,), (,), (,), (,),
(,),…, (,), (,),…, (,) }
Probabilità 02 - 10 / 53
Necessità di approccio corretto e rigoroso
S = { (,), (,), (,), (,), (,),
(,),…, (,), (,),…, (,) }
• Definiamo poi i seguenti eventi:
– E1: la prima pallina estratta sia bianca
– E2: la seconda pallina estratta sia bianca
– E3: la prima pallina estratta sia bianca e la seconda sia nera
– E4: la prima e la seconda pallina estratte siano entrambe bianche
– E5: la somma dei numeri delle palline estratte sia uguale a 5
– E6: la somma dei numeri delle palline estratte sia minore o uguale a 5
– E7: la somma dei numeri delle palline estratte sia minore o uguale a 4
– E8: la somma dei numeri delle palline estratte sia minore o uguale a 10
– E9: la somma dei numeri delle palline estratte sia uguale a 10
Probabilità 02 - 11 / 53
Necessità di approccio corretto e rigoroso
S = { (,), (,), (,), (,), (,),
(,),…, (,), (,),…, (,) }
• Lo spazio campione S è finito
ed è composto da 20 “punti campione”:
# S = N = 20
• I punti campione sono equiprobabili pertanto:
P  s1  P  s2     P  sN   1 N
• Se si introduce la funzione
P Ei  
# Ei
#S
è abbastanza agevole verificare che essa soddisfa i 3 assiomi di
Kolmogoroff ed è pertanto una funzione di probabilità.
Probabilità 02 - 12 / 53
Necessità di approccio corretto e rigoroso
• La funzione di probabilità definita ci permette di individuare la
probabilità che “la prima pallina estratta sia bianca”, cioè la
probabilità dell’evento E1.
S = { (,), (,), (,), (,), (,),
(,),…, (,), (,),…, (,) }
: # S = 20
E1 = {(,), (,), (,), (,),
(,), (,), (,), (,) }
P
8
E1  

#S
20
# E1
: # E1 = 8
Probabilità 02 - 13 / 53
Necessità di approccio corretto e rigoroso
S = { (,), (,), (,), (,), (,),
(,),…, (,), (,),…, (,) }
• Definiamo poi i seguenti eventi:
– E1: la prima pallina estratta sia bianca
– E2: la seconda pallina estratta sia bianca
– E3: la prima pallina estratta sia bianca e la seconda sia nera
– E4: la prima e la seconda pallina estratte siano entrambe bianche
– E5: la somma dei numeri delle palline estratte sia uguale a 5
– E6: la somma dei numeri delle palline estratte sia minore o uguale a 5
={(
), (
), (
), (
)}
– E7: la somma dei numeri delle palline estratte sia minore o uguale a 4
– E8: la somma dei numeri delle palline estratte sia minore o uguale a 10
– E9: la somma dei numeri delle palline estratte sia uguale a 10
S
●,●
●,○
○,●
○,○
Probabilità 02 - 14 / 53
Necessità di approccio corretto e rigoroso
S = { (●,●), (●,○), (○,●), (○,○) }
• Definiamo poi i seguenti eventi:
– E1: la prima pallina estratta sia bianca
– E2: la seconda pallina estratta sia bianca
– E3: la prima pallina estratta sia bianca e la seconda sia nera
– E4: la prima e la seconda pallina estratte siano entrambe bianche
Probabilità 02 - 15 / 53
Necessità di approccio corretto e rigoroso
• individuata la probabilità
p
j
di
ciascun punto campione:
p = P [{ s }]
 p =1
j
j
N
con j = 1, 2, … , N e con
j
j 1
• definiamo per ogni evento
Ei S:
P Ei  
• E1: la prima pallina estratta sia bianca
P
2
6
8
E1    
20 20 20
p

j:s j Ei
j
Probabilità 02 - 16 / 53
Necessità di approccio corretto e rigoroso
• definiamo per ogni evento
P E1    p
j:s j E1
P
P Ei  
Ei S:
j
8

20
p

j:s j Ei
8
E1   
# S 20
# E1
Dal confronto dei risultati potremmo dedurre che
Con il processo deduttivo è anche possibile dimostrare che
anche il primo metodo è corretto
60 è divisibile per 7
dato che i risultati sono uguali
j
Probabilità 02 - 17 / 53
Funzione di probabilità
Una funzione di probabilità P è una funzione di insieme che:
– ha per dominio lo spazio degli eventi A ,
– ha per codominio l’intervallo [ 0, 1 ] ,
– soddisfa i 3 assiomi di Kolmogoroff
P E   0
• P S   1
•
E  A
• se E1 , E2 , … , En , ... è una sequenza di eventi mutamente esclusivi
dello spazio degli eventi A e se l’evento unione di tali eventi appartiene
allo spazio degli eventi A, allora la probabilità dell’evento unione è pari
alla somma delle probabilità dei singoli eventi:
P





i 1

Ei  


P
i 1
Ei 
Probabilità 02 - 18 / 53
Variabili casuali
Probabilità 02 - 19 / 53
Variabile casuale
premessa
• Gli spazi campione possono essere insiemi di oggetti, di
grandezze fisiche, di descrizioni, ecc. non necessariamente
trattabili dai comuni operatori matematici.
• Volendo definire dei modelli adatti allo studio di fenomeni
casuali è pertanto opportuno rappresentare gli elementi dello
spazio campione mediante numeri reali.
(T,T) > (T,C) ?
• Per fare ciò dobbiamo stabilire
una corrispondenza fra le
possibili manifestazioni del
fenomeno casuale trattato
e gli elementi di R .
• La applicazione che realizza
questa trasformazione
è la variabile casuale.
Probabilità 02 - 20 / 53
Variabile casuale
definizione:
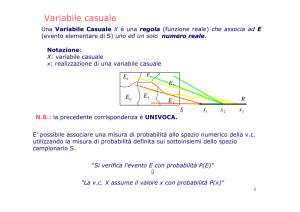
La variabile casuale X è una funzione avente come dominio
lo spazio campione S e come codominio la retta reale, fissato
che sia lo spazio di probabilità ( S, A, P [ ● ] ) in cui si opera.
requisito:
l’insieme di tutti gli elementi
s S tali che la loro
immagine X(s) sia minore
di un determinato x R
deve essere un evento.
x2  E = { s1, s3 }
Probabilità 02 - 21 / 53
Variabile casuale
esempio:
Consideriamo l’esperimento costituito dal lancio (contemporaneo)
di due monete:
S = { (T,T), (T,C), (C,C) }
Definiamo la variabile casuale X come:
il “numero di teste risultanti”:
0

X ( s)   1

2
se s  s0  (C, C)
se s  s1  (T, C)
se s  s2  (T, T )
X ha dominio = S e codominio = { 0, 1, 2 }
Probabilità 02 - 22 / 53
Variabile casuale
0

X ( s)   1

2
se s  s0  (C, C)
se s  s1  (T, C)
se s  s2  (T, T )
requisito:
l’insieme di tutti gli elementi
s S tali che la loro
immagine X(s) sia minore
di un determinato x R
deve essere un evento.
x2 = 2  E = { s0, s1 } =
= “no 2 teste”
Probabilità 02 - 23 / 53
Variabile casuale
Nello spazio campione S
non è rappresentata la
“popolazione dei lanci effettuati”,
ma sono presenti
solo i “possibili risultati”.
Probabilità 02 - 24 / 53
Variabile casuale
“Mappatura” di S
(C,C)

0
(T,C)

1
(C,C)

2
Probabilità 02 - 25 / 53
Popolazione oggetto
• Si definisce “popolazione oggetto” l’insieme di tutti quegli
elementi che hanno in comune almeno una caratteristica.
• Una popolazione oggetto può essere finita o infinita a seconda
che sia composta da un numero finito o infinito di elementi
(persone, oggetti, misure, osservazioni, …)
• Limitiamo il nostro interesse a quelle caratteristiche comuni agli
elementi della popolazione oggetto
che sono classificabili come
“grandezze misurabili”
(numerali, razionali,
strumentali, selettive,
complesse).
Probabilità 02 - 26 / 53
Popolazione oggetto
Misurazione
Variabile casuale
Probabilità 02 - 27 / 53
Dalla popolazione oggetto
alla variabile casuale
Caratteristica
comune della
popolazione
oggetto
Misure della
caratteristica
comune della
popolazione oggetto
Valori della
variabile casuale X
con
dimensione fisica
con
unità di misura
adimensionale
Probabilità 02 - 28 / 53
Dalla popolazione oggetto
alla variabile casuale
Caratteristica
comune della
popolazione
oggetto
Francesca Piccinini
e Simona Gioli
Misure della
caratteristica
comune della
popolazione oggetto
Valori della
variabile casuale X
h = 1,85 metri
Probabilità 02 - 29 / 53
Dallo spazio campione
alla retta reale
tramite la variabile casuale
definizione:
La variabile casuale X è una funzione avente come dominio lo
spazio campione S e come codominio la retta reale,
fissato che sia lo spazio di probabilità ( S, A, P [ ● ] )
in cui si opera.
convenzione:
Indicheremo con
X(s) la variabile
casuale e con
x i valori che
essa assume
Probabilità 02 - 30 / 53
La modellazione della
popolazione oggetto:
le funzioni di probabilità
e le variabili casuali
Probabilità 02 - 31 / 53
Modello della popolazione oggetto
Le funzioni di probabilità, cioè la
– densità di probabilità fX ( x ) e la
– distribuzione cumulativa di probabilità
FX
( x ),
sono “modelli matematici” con cui si cerca di descrivere la
popolazione oggetto per quanto è attinente al
valore (della misura) della caratteristica comune.
Probabilità 02 - 32 / 53
Funzione di distribuzione cumulativa
definizione:
Data una variabile casuale X si definisce
funzione di distribuzione cumulativa FX ( x )
quella funzione che:
• ha per dominio l’asse reale
• ha per codominio l’intervallo chiuso [ 0 , 1 ]
• ed è definita come:
FX ( x ) = P
[Xx]=P [{s:X(s)x}]
Probabilità 02 - 33 / 53
Funzione di distribuzione cumulativa
FX ( x ) = P
[Xx]=P [{s:X(s)x}]
A rigore:
La funzione di distribuzione cumulativa associa ad ogni
valore x della variabile casuale X la probabilità dell’evento
costituito da tutti i
punti campione s che
s)
minore o uguale ad x .
hanno immagine X (
Probabilità 02 - 34 / 53
Funzione di distribuzione cumulativa
FX ( x ) = P
[Xx]=P [{s:X(s)x}]
In termini semplificati:
La funzione di distribuzione cumulativa associa ad ogni
valore x della variabile casuale X
la somma delle probabilità
dei punti campione s che
s)
minore o uguale ad x .
hanno immagine X (
Probabilità 02 - 35 / 53
Le funzioni
per le
variabili casuali
discrete
Probabilità 02 - 36 / 53
Funzione di distribuzione cumulativa
per una variabile casuale discreta
esempio:
Consideriamo l’esperimento costituito dal lancio (contemporaneo)
di due monete:
S = { (T,T), (T,C), (C,C) }
Sia X la variabile casuale che indica il “numero di teste risultanti”:
0

X ( s)   1

2
se s  s0  (C, C)
se s  s1  (T, C)
se s  s2  (T, T )
X ha dominio = S e codominio = { 0, 1, 2 }
Probabilità 02 - 37 / 53
Funzione di distribuzione cumulativa
per una variabile casuale discreta
spazio campione:
variabile casuale:
probabilità dei
tre punti campione:
P
P
P
S = { (T,T), (T,C), (C,C) }
0 se s  s0  (C, C)

X ( s )   1 se s  s1  (T, C)

2 se s  s2  (T, T )
(s0) = 0,25
(s1) = 0,5
(s2) = 0,25
FX
(x)=
P
[Xx]
Probabilità 02 - 38 / 53
riassumendo: Funzione di distribuzione cumulativa
FX
(x)=
P
0 se s  s0  (C, C)

X ( s )   1 se s  s1  (T, C)

2 se s  s2  (T, T )
[Xx]
P
P
P
(s0) = 0,25
(s1) = 0,5
(s2) = 0,25
Probabilità 02 - 39 / 53
Funzione di densità discreta
definizione:
Data una variabile casuale discreta X avente codominio
{ x1 , x2 , … , xn , … }  R si dice
“ funzione di densità discreta di X ” o “ funzione di probabilità ”
quella funzione fX ( x ) che:
• ha per dominio l’asse reale,
• ed è definita da:
P
f X x   
 0
X  x 
j
se x 
x j , con j  1,2,, n,
se x 
xj
Probabilità 02 - 40 / 53
Funzione di densità discreta
P
f X x   
 0
X  x 
j
se x 
x j , con j  1,2,, n,
se x 
xj
In termini semplificati:
La funzione di densità discreta associa ad ogni
valore x della variabile casuale X la probabilità del
punto campione s che
ha immagine X (
uguale ad x
s)
Probabilità 02 - 41 / 53
Funzione di densità discreta
spazio campione:
S = { (T,T), (T,C), (C,C) }
0 se s  s0  (C, C)

variabile casuale: X ( s )   1 se s  s1  (T, C)

2 se s  s2  (T, T )
probabilità dei
tre punti campione:
P
P
P
(s0) = 0,25
(s1) = 0,5
(s2) = 0,25
 P
f X x   
 0
X  x 
j
se x  x j
se x  x j
Probabilità 02 - 42 / 53
riassumendo: Funzione di densità discreta


 P X  x j se x  x j , con j  1,2,, n,
f X x   
se x  x j
 0
0 se s  s0  (C, C)
P (s0) = 0,25

X ( s )   1 se s  s1  (T, C)
P (s1) = 0,5

2 se s  s2  (T, T )
P (s2) = 0,25
Probabilità 02 - 43 / 53
Funzione di densità discreta
• Gli elementi dell’insieme { x1 , x2 , … , xn , … } 
vengono indicati con il nome di “punti massa”.
R
• La funzione di densità discreta fX ( x ) è una funzione
da R nell’intervallo chiuso [ 0,1 ]
che gode delle seguenti proprietà:
f x x   0, x R
più precisamente:

j
f x x j   1
fX ( x ) > 0 per ogni x = xj e
fX ( x ) = 0 per ogni x  xj
ove la sommatoria è estesa
a tutti punti massa x1 , x2 , … , xn , …
Probabilità 02 - 44 / 53
Legami fra fX e FX ( x )
• La funzione di distribuzione cumulativa FX ( x )
è legata alla funzione di densità discreta
fX
della stessa variabile casuale X dalla relazione:
F
X
(x)

 f x 
X
j: x j  x
j
Probabilità 02 - 45 / 53
Legami fra fX e FX ( x )
funzione di
densità discreta fX ( x )
F
X
(x)

 f x 
X
j
j: x j  x
funzione di distribuzione
cumulativa F X ( x )
Probabilità 02 - 46 / 53
Legami fra fX e FX ( x )
• La funzione di densità discreta
fX
è legata alla
funzione di distribuzione cumulativa
FX ( x )
della stessa variabile casuale X dalla relazione:
 FX x j   lim FX
h 0
f X x   
 0
x
j
 h  se x  x j
 x  xj
Probabilità 02 - 47 / 53
Legami fra fX e FX ( x )
funzione di distribuzione
cumulativa F X ( x )
f X x  
F x j   lim F x j  h
h 0
X

X
funzione di
densità discreta fX ( x )
se x  x j
Probabilità 02 - 48 / 53
Variabili casuali
continue