RACCONTARE LA
MATEMATICA
A scuola da Pitagora
QUANTE PAROLE OCCORRONO PER
SCRIVERE I NOMI DI TUTTI I
NUMERI? Proviamo…
Zero
Uno
Due
Tre
Quattro
Cinque
Sei
Sette
Otto
Nove
Dieci
Undici
Dodici
Tredici
Quattordici
Quindici
Sedici
Diciassette
Diciotto
Diciannove
Venti
Trenta
Quaranta
Cinquanta
Sessanta
Settanta
Ottanta
Novanta
Cento
Mille
Milione
Miliardo
I numeri sono infiniti
ma le parole sono
solo 32!!!
Non è
straordinario?
PITAGORA (570-500 a.C.)
A Pitagora si può attribuire la fondazione
dell'ARITMETICA (dal greco Arithmòs=
Numero) con la quale, mediante i Numeri, è
possibile spiegare ogni cosa: dal mondo che ci
circonda al moto degli astri, al succedersi delle
stagioni, dalle armonie della Musica al ciclo
della vegetazione. Per Pitagora il Numero è
tutto, è l l'elemento di cui tutte le cose sono
costituite.
I Numeri erano divisi in pari e dispari, positivi e
negativi, maschili e femminili.
L'ordine e la perfezione stanno dalla parte dei
numeri dispari, mentre , al contrario, il
disordine ed il male stanno sempre dalla parte
dei pari
LA SCUOLA PITAGORICA
Pitagora fondò una scuola a
Crotone(Magna Grecia) alla quale
erano ammesse anche le
donne(fatto assai strano per
quell’epoca!)
Era una sorta di società segreta
dove venivano imposte delle regole
di vita molto rigide ad es. erano
tutti vegetariani)
LA SCUOLA DI ATENE
Uno dei simboli della
scuola pitagorica era il
PENTAGONO STELLATO
si disegna
tracciando tutte
le diagonali
possibili di un
pentagono
regolare fino ad
ottenere una
stella a 5 punte.
L’ARITMOGEOMETRIA
Per aritmogeometria si intende la
sintesi fra aritmetica (scienza dei soli
numeri) e geometria (scienza delle
sole figure).
Con il termine numero Pitagora
intendeva qualcosa di completo: la
dimensione essenziale delle cose
In altri termini Pitagora assegnò un
significato spaziale ai numeri. Ve ne
sono così di triangolari, di quadrati, di
pentagonali,…
NELL’ ARITMOGEOMETRIA
1, la Monade rappresenta la Ragione, l’Uno, il principio
primo, è considerato impari cioè né pari né dispari e
geometricamente rappresenta il punto.
2, la Diade rappresenta la parte femminile, l’indefinito e
illimitato, l’opinione (sempre duplice) e
geometricamente la linea.
3, la Triade rappresenta la parte maschile, il definito e
limitato e geometricamente il piano.
4, la Tetrade rappresenta la giustizia in quanto divisibile
equamente da entrambe le parti.
5, la Pentade, rappresenta lo sposalizio poiché è la
somma della parte femminile (2) e maschile (3),
simboleggia la vita e il potere; il pentagramma è il
simbolo dei pitagorici.
TETRAKTYS
10, la Decade è il numero perfetto,
la fonte e radice dell’eterna natura
perché il 10 “contiene” l’intero
universo essendo la somma di
1,2,3 e 4; esso veniva
rappresentato con la tetractys, il
triangolo equilatero di lato 4, sul
quale veniva fatto il giuramento di
adesione alla scuola pitagorica.
NUMERI
TRIANGOLARI
Come si ottengono i numeri
triangolari (con i numeri)
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
....
Come si ottengono i numeri
triangolari (con le figure)
Come si ottengono i
numeri triangolari
(con le parole)
SOMMANDO
SUCCESSIVAMENTE
I NUMERI NATURALI
NUMERI
QUADRATI
Come si ottengono i numeri
quadrati (con i numeri)
1=1x1=1
1+3=2x2=4
1+3+5=3x3=9
1+3+5+7=4x4=16
1+3+5+7+9=5x5=25
1+3+5+7+9+11=6x6=36
....
Come si ottengono i numeri
quadrati (con le figure)
Come si ottengono i
numeri quadrati
(con le parole)
SOMMANDO
SUCCESSIVAMENTE
I NUMERI DISPARI
RELAZIONE FRA NUMERI
QUADRATI E NUMERI
TRIANGOLARI (con i numeri)
4=1+3
9=3+6
16=6+10
25=10+15
36=15+21
…
Relazione
fra numeri
triangolari
e numeri
quadrati
(con le
figure)
RELAZIONE FRA NUMERI
QUADRATI E NUMERI
TRIANGOLARI (con le parole)
LA SOMMA DI 2
NUMERI TRIANGOLARI
SUCCESSIVI
E’ SEMPRE
UN NUMERO
QUADRATO
NUMERI
RETTANGOLARI
Come si ottengono i numeri
rettangolari (con i numeri)
2=2
2+4=6
2+4+6=12
2+4+6+8=20
2+4+6+8+10=30
….
Come si ottengono i numeri
rettangolari (con le figure)
Come si ottengono i
numeri rettangolari
(con le parole)
SOMMANDO
SUCCESSIVAMENTE
I NUMERI PARI
RELAZIONE FRA NUMERI
RETTANGOLARI E NUMERI
TRIANGOLARI (con i numeri)
1+1=2
3+3=6
6+6=12
10+10=20
15+15=30
…
Relazione fra numeri
triangolari e numeri
rettangolari (con le figure)
RELAZIONE FRA NUMERI
RETTANGOLARI E NUMERI
TRIANGOLARI (con le parole)
UN NUMERO
RETTANGOLARE
E’
LA SOMMA DI DUE
TRIANGOLARI
UGUALI
….E CON LE FORMULE
Numeri quadrati: nxn=n²
Numeri rettangolari: nx(n+1)
Numeri triangolari:nx(n+1)/2
SCOPRIAMO
ALCUNE
PROPRIETA’
QUADRATI DEI NUMERI CHE
TERMINANO CON LA CIFRA 5
5² =25; 15² =225; 25² =625;
35² =1225…
Finiscono tutti con 25
Le cifre prima del 25 (0, 2, 6,
12…) si ottengono
moltiplicando la cifra che
nella base precede il 5 (0, 1,
2, 3,…) per il suo
successivo: 0x1=0; 1x2=2;
2x3=6; 3x4=12…
QUANTI TRIANGOLI NEI
NUMERI TRIANGOLARI?
CONTIAMO
1 (0=0x0)
3 (1=1x1)
6 (4=2x2)
10 (9=3x3)
15 (16=4x4)
….
SONO NUMERI QUADRATI!!!
ULTIMA CIFRA DEI
NUMERI QUADRATI
0
Sì
1
Sì
2
No
3
No
4
sì
5
Sì
6
Sì
7
No
8
No
9
sì
OGNI NUMERO QUADRATO
O E’ UN MULTIPLO DI 5
O UN SUO PRECEDENTE
O UN SUO SUCCESSIVO
1=0X5=0
4=1X5-1=5-1
9=2X5-1=10-1
16=3X5+1=15+1
25=5X5=25
36=7X5+1=35+1
49=10x5-1=50-1
NUMERI PENTAGONALI
Come si ottengono i numeri
pentagonali (con i numeri)
1=1
1+4=5
1+4+7=12
1+4+7+10=22
1+4+7+10+13=35
....
Come si ottengono i
numeri pentagonali
(con le figure)
Come si ottengono i
numeri pentagonali
(con le parole)
1-5-12-22-35….
La differenza di 2
numeri successivi
parte da 4 e
aumenta sempre di 3
NUMERI ESAGONALI
Come si ottengono i numeri
esagonali (con i numeri)
1=1
1+6=7
1+6+12=19
1+6+12+18=37
....
Come si ottengono i numeri
esagonali (con le figure)
Come si ottengono i
numeri esagonali
(con le parole)
1-7-19-37…
La differenza di 2
numeri successivi
partendo da 6
aumenta sempre di 6
NUMERI
MEMORABILI
NON SOLO
PITAGORICI
10 PUNTI IN 5 FILE DA 4
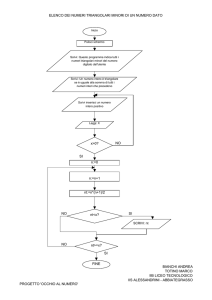
INDOVINA IL NUMERO
25 10 21 100 64 28 35 40 3 37
È un numero figurato
25 10 21 100 64 28 3
È un numero triangolare
10 21 28 3
È un multiplo di 7
21 28
È divisibile per 4
28
Roma, palazzo delle esposizioni
16 ottobre 2014
31 maggio 2015
“ non tutto ciò che conta può
essere contato”
DA ZERO A INFINITO....
BUON VIAGGIO!