Chimica Generale e Inorganica
Termodinamica
Studio delle variazioni di energia coinvolte nelle trasformazioni di un
sistema
ENERGIA: proprietà di ogni corpo, la capacità di compiere un lavoro
o di fornire calore
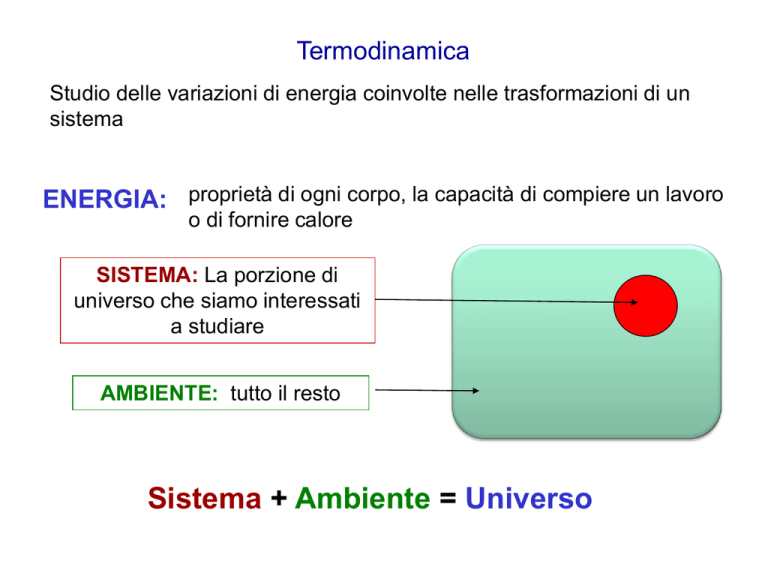
SISTEMA: La porzione di
universo che siamo interessati
a studiare
AMBIENTE: tutto il resto
Sistema + Ambiente = Universo
Chimica Generale e Inorganica
Chimica Generale e Inorganica
La termodinamica non da informazioni sul meccanismo e sui tempi di un
processo ma prevede se questo può avvenire.
Funzioni di stato (variabili di stato):
DX = Xfinale - Xiniziale
il loro valore dipende solo dallo stato
del sistema e non dalla natura del
processo che il sistema ha compiuto
per raggiungere quello stato.
maggiore E potenziale
h
Un esempio di variabile di
stato: l’altezza o altitudine
minore E potenziale
Chimica Generale e Inorganica
Variabili di stato
ESTENSIVE
INTENSIVE
Dipendono dalla quantità
di materia considerata
Indipendenti quantità di materia
considerata
Sono additive
NON sono additive
Volume, Massa, Calore
Temperatura, Pressione, Densità
equazioni di stato
leggi che correlano le variabili di stato
PV = nRT equazione di stato dei gas ideali
Chimica Generale e Inorganica
Legge di conservazione dell’energia:
l’energia non può essere né creata né distrutta, ma può solo
trasformarsi da una forma in un’altra, o trasferirsi dal sistema
all’ambiente circostante.
DE sistema = - DE ambiente circostante
Energia cinetica
energia associata al movimento di un corpo
Energia potenziale
energia che dipende dalla posizione in un campo
Energia di legame
energia necessaria per spezzare una mole di legami
Energa nucleare
energia che tiene assieme i nucleoni
Energia interna
Energia totale che un sistema possiede (somma di
tutte le forme di energia)
Chimica Generale e Inorganica
ENERGIA INTERNA (E)
per un gas l’energia interna è la somma di vari di vari tipi di energia : traslazionale,
rotazionale, vibrazionale, elettrostatica, di legame…. etc…
L’energia interna è funzione di stato : il valore dipende solo dai valori dei
parametri di stato del sistema e non da come il sistema ha raggiunto quello stato.
In una trasformazione da uno stato iniziale a uno finale si ha :
DE = Ef - Ei
Chimica Generale e Inorganica
In un sistema, l’energia interna E varia quando tra sistema e ambiente c’è
scambio di materia e/o energia.
lavoro
l’energia è scambiata in due modi
calore
il lavoro include tutte le forme di energia eccetto il calore!
I° principio della termodinamica:
In ogni processo, la variazione di energia interna del sistema chiuso è
uguale alla differenza tra il calore (Q) e il lavoro (W) scambiato dal
sistema con l’ambiente.
DE = Q - W
L’energia interna è una funzione di stato, non dipende dal cammino percorso.
Chimica Generale e Inorganica
Convenzione adottata: criterio storico
DE = Q - W
Qacquistato > 0 calore che entra nel sistema (processo endotermico)
Qceduto < 0 calore che esce dal sistema (processo esotermico)
Wacquistato > 0 lavoro fatto dal sistema sull’ ambiente
Wceduto < 0 lavoro fatto dall’ambiente sul sistema
+w
-w
Wespans = PDV
+Q
-Q
Il lavoro di espansione effettuato
dal sistema corrisponde ad un
aumento di volume (V2 > V1)
Chimica Generale e Inorganica
criterio storico (il lavoro fatto dal sistema è positivo, punto di vista utilitaristico )
-w
+w
DE = Q - W
Wespans = PDV
-Q
+Q
criterio egoistico del sistema (è positivo tutto ciò che entra nel sistema, negativo
ciò che esce)
-w
+Q
+w
DE = Q + W
Wespans = - PDV
-Q
Chimica Generale e Inorganica
Il calore Q (flusso di calore)
È una particolare forma di energia che viene trasmessa ai sistemi
circostanti, in seguito ad una differenza di temperatura.
ambiente T <
sistema
sistema
TT>>
Il calore non è una funzione di stato!
T>
T<
Chimica Generale e Inorganica
Il lavoro W
Il lavoro è una forma di energia e può essere
di diversa natura.
Lavoro meccanico = forza • spostamento
Lavoro
meccanico
lavoro pressionevolume
Lavoro elettrico
Fs
PDV
Eq
In termodinamica è molto importante il lavoro
legato alle espansioni o compressioni di volume
La pressione è una forza
per unità di superficie:
F
W F s A s P DV
A
s = spostamento
A = area
F
P
A
1 (litri • atm) = 101.03 J
Chimica Generale e Inorganica
Lavoro di espansione di un gas : lavoro pressione-volume
Il lavoro durante un’espansione da un volume 1 (a P1) a volume 2 (a P2) è somma
dei lavori infinitesimi corrispondenti alle espansioni infinitesime
W Pest dV
Il lavoro totale è la somma integrale dei lavori infinitesimi
Se Pest =cost
W
V2
V1
Pest dV Pest dV Pest V2 - V1 Pest DV
V2
V1
W=P2DV
W=0
W=0
Il lavoro compiuto dipende
dal modo in cui avviene la
trasformazione:
Abbiamo dimostrato che il
lavoro non è una funzione
di stato!
Wa = P2 (V2-V1)
Wb = P1 (V2-V1)
Chimica Generale e Inorganica
Trasformazioni in cui l’unica forma di lavoro è di compressione o espansione
1. Trasformazioni a volume costante
∆E = Q - W = QV - P∆V
Se una reazione viene effettuata a
volume costante (recipiente chiuso),
non si compie lavoro: PDV = 0
∆E = QV
2. Trasformazioni a pressione costante
∆E = Q – W = QP - P∆V
E2 – E1 = QP – P(V2-V1)
E2 – E1 = QP – PV2 + PV1
(E2 + PV2 ) - (E1 + PV1 ) = QP
definendo: H = E + PV
H2 – H1 = QP
∆H = QP
Il calore scambiato in una
reazione chimica che avviene a
volume costante è uguale alla
variazione di energia interna del
sistema
Il calore scambiato in una reazione
chimica che avviene a pressione
costante è uguale alla variazione di
entalpia del sistema
Chimica Generale e Inorganica
Termochimica
si interessa dell’applicazione del I° principio della
termodinamica alle reazioni chimiche e in particolare
alla determinazione dei calori di reazione
Come si esprime il flusso di calore: Q
Caloria (cal): la quantità di calore richiesta per
aumentare di un grado Celsius la temperatura di 1 g di
H2O da 14.5°C a 15.5 °C
1 cal = 4.184 J
1 kcal = 4.184 kJ
Joule (J): da James Joules (1818-1889)
C (capacità termica): quantità di calore richiesta per
Q = C Dt
aumentare di 1°C la temperatura del sistema.
c (calore specifico): quantità di calore richiesta per aumentare di 1°C la
temperatura di un grammo di una sostanza.
Per una sostanza di massa m
Q = mc Dt
Chimica Generale e Inorganica
equazione termochimica = equazione chimica bilanciata con l’indicazione
dell'entalpia di reazione
Reazione esotermica: combustione
CH4(g) + 2 O2(g) CO2(g) + 2H2O(l)
Qp = DH = - 890 kJ/mol
calore ceduto a pressione
costante nella combustione di
1 mole di CH4
Reazione endotermica: decomposizione
CaCO3(s) CaO(s) + CO2(g)
Qp = DH = + 11,8 kJ/mol
calore assorbito a pressione
costante per 1 mole di CaCO3
gas
Chimica Generale e Inorganica
DHsubl= DHfus + DHevap
Energia interna
trasformazioni endotermiche
DH evaporaz
liquido
DH sublimaz
DH fusione
solido
DH di fusione
DH di sublimazione
DH di evaporazione
quantità di calore necessaria per portare una mole di
sostanza dallo stato solido a liquido o gassoso, e
dallo stato liquido a gassoso, è sempre positiva:
trasformazioni esotermiche
DHbrinam= DHliquefaz + DHsolidif
Energia interna
gas
DH liquefaz
liquido
DH brinam
DHsolidificaz
solido
Chimica Generale e Inorganica
Reazioni di dissociazione:
H2(g) 2 H(g)
DH° = + 436 kJ
Cl2(g) 2 Cl(g)
DH° = + 243 kJ
viene sempre assorbita energia quando vengono rotti dei legami chimici.
Formazione di legami:
Al contrario viene sempre rilasciata energia quando si formano dei legami tra
atomi (si passa ad un sistema più stabile) :
H(g) + Cl(g) HCl(g)
DH° = - 431 kJ
H(g) + F(g) HF(g)
DH° = - 565 kJ
Chimica Generale e Inorganica
Proprietà dell’entalpia :
1. il DH dipende dallo stato fisico: occorre sempre indicare lo stato fisico delle
sostanze
2H2(g) + O2(g) 2H2O(g)
DH° = -483,74 kJ (calore ceduto)
2H2(g) + O2(g) 2H2O(l)
DH° = -571,70 kJ
2. Il DH dipende dalla quantità di reagenti che si trasformano: se l'equazione
chimica viene moltiplicata per un fattore, il DH va moltiplicato per lo stesso
fattore
H2(g)+ 1/2O2(g) H2O(g)
DH° = 1/2 x -483,74 kJ= -241,87 kJ
3. il DH cambia segno se si inverte l'equazione chimica (il calore viene scambiato
nel senso opposto)
2H2O(g) O2(g) + 2H2 (g)
H2O(s) H2O(l)
H2O(l) H2O(s)
DH°= +483,74 kJ
DH°fus = + 6.00 kJ calore di fusione
DH°solidific = - 6.00 kJ
calore di solidificazione
Entalpia standard di formazione, DH°f ( o H°f )
Chimica Generale e Inorganica
Calore scambiato nella reazione di formazione di 1 mole di composto in condizioni
standard a partire dagli elementi in condizioni standard.
C(grafite) + O2 (g) CO2(g)
DHf° = -393.5 kJmol-1
H2(gas) + 1/2O2 (g) H2O(l)
DHf°= -285 kJmol-1
H2 (gas, 1 atm, 25°C) + 1/2O2 (gas, 1 atm, 25°C) H2O(liq, 1 atm, 25°C)
Reazione di formazione del nitrato di ammonio e a 25°C e 1 atm
N2(g) + 2 H2 (g) + 3/2 O2 NH4NO3(s)
Per convenzione l’entalpia di
formazione di tutti gli elementi
nel loro stato standard è pari a
zero:
DHf° = -365.6 kJmol-1
entalpia di formazione di una mole di cloro gas = 0
entalpia di formazione della grafite = 0
la grafite è la forma allotropica più stabile del C a 1 atm e 25°C.
C(graf) C(diamante)
DH°f(grafite)= 0 ; DH°f(diamante)= 1,9 kJ/mol
Chimica Generale e Inorganica
Legge di Hess
“In una reazione chimica il calore scambiato a pressione
costante è indipendente dagli stadi intermedi attraverso i
quali si evolve il sistema e dipende solo dal suo stato
iniziale e finale”
La legge di Hess è una conseguenza del principio di conservazione dell’energia.
Diagramma entalpico
H
Hniz
Per un'equazione chimica A C che può
essere scritta come la somma di due o più
stadi, A B C, DH per l'equazione totale è
uguale alla somma dei DH per gli stadi singoli.
DHreaz = DH1 + DH2
Per n stadi:
Hfin
DH = DH1 + DH2 + DH3 +…
Chimica Generale e Inorganica
reazione di ossidazione della grafite
C(grafite) + O2 (g) CO2(g)
DH°1= -393,5 kJ
A parità di pressione e temperatura la variazione di entalpia può
essere ottenuta dalla somma delle due reazioni successive:
C(grafite) + 1/2 O2 (g) CO(g)
DH°2= -110.5 kJ
CO(g) + 1/2 O2 (g) CO2(g)
DH°3= -283,0 kJ
C(grafite) + O2 (g) CO2(g)
DH°1= -393,5 kJ
DH°1 = DH°2 + DH°3
Chimica Generale e Inorganica
reazione di formazione del benzene
6 C(grafite) + 3 H2 (g) C6H6(l)
DH°f = ?
C(grafite) + O2 (g) CO2(g)
DH°C1 = -393.5 kJ
H2(g) + 1/2 O2(g) H2O(l)
DH°C2 = -285,8 kJ
C6H6(l) + 15/2 O2(g) 6CO2(g) + 3H2O(l)
DH°C3 = -3268,0 kJ
6 C(grafite) + 6 O2(g) 6 CO2(g)
3H2(g) + 3/2O2(g) 3 H2O(l)
DH°1 = 6DH°C1= 6(-393.5) kJ
DH°2 = 3DH°C2= 3(-285,8) kJ
6 CO2(g) + 3H2O(l) C6H6(l) + 15/2O2 (g) DH°3 = -DH°C3= +3268,0 kJ
6 C(grafite) + 3 H2 (g) C6H6(l)
DH°f(C6H6)= + 49.6 kJ
Calcolo di DH° di reazione usando i DH°f
Applicazione della legge di Hess :
una reazione reagenti prodotti
può essere scritta come somma delle reazioni di
formazione dei prodotti e dei reagenti (l’entalpia
di formaz dei reagenti presa nel senso opposto)
Chimica Generale e Inorganica
reagenti
DH°reaz
prodotti
DH°f
reagenti
DH°f
prodotti
reagenti elementi prodotti
DH°reaz = - DHf reag + DHf prod
elementi
ΔH reaz ΣiΔH f (prodotti)- ΣiΔH f (reagenti)
ΔH reaz ΣiH f (prodotti)- ΣiH f (reagenti)
Si può trovare
scritta in
entrambi i modi
i = coefficienti stechiometrici
2 C8H18(l) + 25 O2 (g) 16 CO2(g) + 18 H2O(g)
DH°reaz = (16DHf°CO2 + 18DHf°H2O)-(2DHf°C8H18 – 25DHf°O2)
Chimica Generale e Inorganica
Esercizio: Calcolare il valore di DH della reazione: 2 C(grafite) + O2(g) 2 CO(g)
noti i DH° delle reazioni:
C(grafite) + O2 (g) CO2(g)
DH°1= -393,5 kJ/mole
2CO(g) + O2(g) 2CO2(g)
DH°2= -566,0 kJ/mole
Soluzione:
2C(grafite) + 2 O2(g) 2CO2(g)
2CO2(g) 2CO(g) + O2 (g)
____________________________
2C(grafite) + O2 (g) 2CO(g)
2 (-393.5) kJ
- (- 566.0) kJ
- 221.0 kJ
Chimica Generale e Inorganica
Esercizio: Determinare il DH° per la reazione
noti i DH° di formazione per i due composti:
H2O(g) H2O(l)
H2(g) + ½ O2(g) H2O(g)
DH°f(H2O(g)) = - 241,8 kJ/mol
H2(g) + ½ O2(g) H2O(l)
DH°f(H2O(l)) = - 285,8 kJ/mol
H2O(g) H2(g) + ½ O2(g) -DH°fH2O(g)= +241.8 kJ/mol
H2(g) + ½ O2(g) H2O(l) DH°fH2O(l) = -285.8 kJ/mol
H2O(g) H2O(l)
DH°reaz = - 44.0 kJ/mol
In alternativa, utilizzando i DH°f di formazione:
DH°reaz = DH°f(prodotti) - DH°f(reagenti) = DH°f(H2O(l)) - DH°f(H2O(g)) =
= -285.8 – (- 241.8) = - 44.0 kJ/mol
Chimica Generale e Inorganica
Esercizio: Data l'equazione termochimica a P = costante
CH4(g) + 2O2(g) CO2(g) + 2H2O(l)
DH° = -890,3 kJ
Quanto calore si può ottenere dalla combustione di 14,1 L di metano (d=0.71 gL-1),
assumendo che l'ossigeno sia in eccesso?
nCH 4
massa( g ) 14.1 L 0.71 g L-1
0.626 mol
-1
( MM )CH 4
16.0 g mol
Q n CH 4 ΔH 0.626 mol (-890 kJ mol -1 ) -557.3 kJ
Quanto metano è necessario per produrre 1000 kJ?
Calcolo il numero di moli di metano da bruciare:
nCH 4
m assa
CH
4
1000 kJ mol -1
1.123 mol
-1
- 890 kJ mol
1 ,1 2 3 m o l 1 6 ,0 g / m o l 1 8 ,0 g
Chimica Generale e Inorganica
Esercizio:
1) Determinare il calore in gioco nella seguente reazione (a pressione costante) di
1000 g di CH4 con eccesso di O2:
CH4(g) + O2(g) C(diamante) + 2 H2O(l)
sapendo che DH°f(H2O(l))=-285.8 kJ/mol, DH°f(CH4)=-74.9 kJ/mol,
DH°f(C(diamante)) = + 1.8 kJ/mol.
2) Dire se la reazione è esotemica o endotermica.
DH°reaz= [2DH°f(H2O(l) + DH°f(C(diamante))] - [DH°f(CH4) + DH°f(O2)]
= [-2x285.8 + 1.8]-[-74,9 + 0] = -494.9 kJ
DH < 0 reazione esotermica
n(CH4) = 1000 g / 16.05 g/mol = 62.31 mol di CH4
62.31 mol x (-494.9 kJ/mol) = -30 837 kJ = - 30.84x 103 kJ
Chimica Generale e Inorganica
Noti i DH°f dei composti presenti, calcolare il DH° per la seguente reazione:
CH4(g) + 4 Cl2(g) CCl4(l) + 4 HCl(g)
dire se la reazione è esotermica o endotermica e calcolare la quantità di calore in
gioco nella formazione di 200 L di HCl, misurati a condizioni standard.
1)
DH°reaz= [1 DH°f(CCl4) + 4 DH°f(HCl)] - [1 DH°f(CH4) + 4 DH°f(Cl2)] =
=[1(-139) + 4(-92,3)] - [1(-74,9) + 4(0)] = - 433 kJ
2) Oppure: Scrivendo in colonna le reazioni di formazione dei prodotti e quelle di
formazione dei reagenti (queste nel senso inverso) si ha:
CH4(g) C(graf) + 2H2(g)
-DH°f = -(-74,9 kJ/mol )
C(graf) + 2Cl2(g) CCl4(l)
DH°f = (-139 kJ/mol)
2H2(g) + 2Cl2(g) 4HCl (g)
4xDH°f = 4(-92,3 kJ/mol)
CH4(g) + 4Cl2(g) CCl4(l) + 4HCl(g)
DH°reaz= - 433 kJ
n(HCl)= PV/RT = 200 L * 1 atm/ 0.0821 L atm (mol K-1) (273.15+25) K = 8.17 mol
Q = (- 433 kJ / 4 molHCl ) * 8.17 molHCl = - 884.4 kJ
Chimica Generale e Inorganica
Esercizio: combinare i seguenti dati termochimici
S(s) + O2(g) SO2(g)
DH= -297 kJ
2 SO3(g) 2 SO2(g) + O2(g) DH= +198 kJ
per ottenere il DH°f di SO3:
soluzione (1):
(1)
(2)
S(s) + 3/2 O2(g) SO3(g)
DH°f= ?
applico Hess alla reazione (2):
2 DH°f(SO2) + DH°f(O2) – 2 DH°f(SO3) = + 198 kJ
2 (-297) + 0 – 2 DH°f(SO3) = + 198 kJ
Da questa espressione ricavo DH°f(SO3):
DH°f(SO3) = 198-(-2x297) / (-2) = -396 kJ/mol
soluzione (2):
2 SO2(g) + O2 2 SO3(s)
DH1 = -1(+198)= -198 kJ
2 S(s) + 2 O2(g) 2 SO2(g)
DH2 = 2(-297)= -594 kJ
2S(s) + 3O2(g) 2SO3(g)
DH3= -594 -198= -792 kJ
Divido per 2:
S(s) + 3/2O2(g) SO3(g)
DH3/2= -792/2 = -396 kJ/mol = DH°f(SO3)












