gauss - Liceo Classico Scientifico XXV Aprile

TEOREMA DI GAUSS PER IL CAMPO ELETTROSTATICO
Premessa:
Fino ad ora abbiamo studiato le cariche ferme, senza correnti. La parola stessa elettrostatiche
presume che le cariche siano statiche.
Definizione di flusso di un vettore attraverso una superficie: 
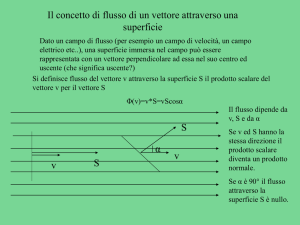
consideriamo una superficie su cui agisce un campo vettoriale A

A = vettore che rappresenta il campo
vettoriale.

n = vettore particolare, chiamato versore*
 = angolo che si forma tra i due vettori
Definizione flusso

 s ( A)  A  S  cos( )

 s ( A) si legge flusso del vettore A attraverso la superficie S.
A = modulo del vettore del campo.
S = superficie
La formula in realtà contiene anche il fattore n (rappresentante il modulo del versore),
ma dato che questo è 1, non si scrive.
*versore: è un particolare vettore che viene sempre considerato avente modulo uno e
perpendicolare alla superficie
Esempio di flusso.
Consideriamo una sezione di una tubatura d’acqua. Possiamo facilmente immaginare che in ogni
particella d’acqua ci sia un vettore velocità. Consideriamo in particolare il vettore velocità sulla
superficie S, con il vettore corrispondente.
Dato che il versore è sempre
perpendicolare alla superficie come lo è
 

anche il vettore V , V ed n coincidono
L’angolo che si viene a formare tra i due
vettori è quindi nullo.  =0
www.easymaths.altervista.org
Quindi sostituendo nella formula del flusso:

 s ( A)  V  S  cos( 0)  V  S
Notare che la formula ottenuta è uguale alla portata. Q  V  S
Teorema di Gauss (per il campo elettrostatico)
Consideriamo una superficie sferica al centro del
quale è racchiusa una carica Q positiva che genera
un campo, che viene rappresentato (per
definizione) con dei vettori uscenti dalla sfera.
Come si può calcolare il flusso in questa
situazione?
Immaginiamo di dividere l’intera superficie della
sfera in tante piccole parti (nel disegno per
comodità ne sono state disegnate 3). Chiamiamo
ogni parte S n
E’ ora facile immaginare che il flusso complessivo è dato dalla somma di tutti i singoli flussi
calcolati per ogni S n , secondo la formula:




 S ( E )   S1 ( E )   S 2 ( E )   S 3 ( E )  ..........
Esaminiamo ora il flusso di una singola superficie S n .

Consideriamo il vettore E come se partisse dalla superficie
(cioè per ragioni algebriche perpendicolare alla superficie)

Disegniamo il versore n , che essendo per definizione

perpendicolare alla superficie coincide con il vettore E .
L’angolo tra i due vettori è quindi nullo.
Da queste considerazioni possiamo dedurre che il flusso di una singola superficie S n è la
seguente:

 Sn ( E )  E  S n  cos( 0)  E  S n
Fatte queste considerazioni, riscriviamo la formula del flusso totale, sostituendo ogni singolo flusso
con la formula appena ricavata:

 S ( E )  E  S1  E  S 2  E  S 3  ..........  E  (S1  S 2  S 3  .......)
Raccogliendo il fattore E, è facile notare come all’interno della parentesi ci sia la somma di tutte le
singole superfici S n , che sommate sono in realtà l’intera superficie della sfera.
www.easymaths.altervista.org
Riscriviamo quindi la formula scrivendo al posto della somma la formula per la superficie di una
sfera, e al posto di E la formula del campo.

 S (E) 
1
Q
Q
 2  4   r2 
4    0 r
0

Q
Abbiamo ricavato il teorema di Gauss:  S ( E ) 
0
Osservazioni:
Il teorema vale sempre, anche se la superficie non è sferica, l’importante è che sia chiusa.
Scomponendo la K in
1
, si riescono ad eseguire importanti semplificazioni.
4   0
Il teorema di Gauss, al contrario della legge di Coulomb, è di facile sperimentazione e
misurazione. Dato lo stretto legame che queste due formule hanno (legge Coulomb 
campo elettrostatico  teorema di Gauss), automaticamente sperimentando l’esattezza del
teorema di Gauss, dimostriamo anche la correttezza della legge di Coulomb.
Teorema di Gauss generalizzato:

Qi
 S (E) 
0
Il teorema di Gauss può anche essere scritto come sommatoria algebrica di tutte le cariche presenti
all’interno della superficie.
CONSEGUENZE DEL TEOREMA DI GAUSS
1) All’interno di un conduttore carico in equilibrio elettrostatico ( cariche ferme) il
campo elettrico è zero in ogni punto.
N.B. Si considera sempre una superficie tridimensionale (di
qualunque forma) chiusa.
Sulle cariche interne non agiscono forze, perciò il campo è nullo.
www.easymaths.altervista.org
2) In un conduttore carico in equilibrio elettrostatico le cariche si trovano solo sulla
superficie esterna.

Qi
In formule: se E  0   s ( E )  0 
 0 quindi: Qi  0 . Ciò vuol dire che se la somma
0
delle cariche interne è nulla, allora se ci sono cariche queste si trovano solo sulla superficie
esterna.
3) Tutti i punti del conduttore si trovano allo stesso potenziale: la sua superficie è quindi
equipotenziale.
poiché all’interno E=0, anche il lavoro tra A e B varrà
0.

Ricordiamo che sulla superficie E è sempre
perpendicolare alla stessa.
L AB  0  q  (V A  VB )  0  V A  V B
Quindi tutti i punti della superficie sono allo stesso
potenziale.
Osservazioni:
Definizione di densità superficiale di carica ( ) :  
carica Q

in C 2 dove S è l’area
m
area
S
Q
. Il fatto che σ sia inversamente
4  r2
proporzionale a r2 vale sempre, qualunque sia la forma della superficie che consideriamo.
Possiamo quindi distinguere due casi:
o la superficie. Se il conduttore è sferico  
Raggio (r)
curvatura
σ GRANDE
piccolo
grande
σ PICCOLO
grande
piccolo
Dato che il campo elettrostatico E è direttamente proporzionale alla densità superficiale di
carica (σ), E è più grande dove σ è più grande.
Considerazioni:
Q
E
r 2  k  4 Abbiamo quindi dimostrato
E   , infatti:

Q

4   r 2
che esiste una proporzionalità diretta tra E e σ. Quindi ecco spiegato
perché gli oggetti appuntiti attirano i fulmini: avendo una grande
curvatura, hanno sulla loro superficie una grande quantità di cariche (σ
grande), che attirano quelle del fulmine.
k
www.easymaths.altervista.org
Definizione di curvatura di una curva:  
1
(  è una lettera greca che si legge
r
“ro”).
Disegnando un qualsiasi percorso non rettilineo, possiamo, per
ogni punto, disegnarne una circonferenza che meglio approssimi
l’andamento curvilineo di quel tratto. Nella figura, si può notare
come in prossimità di una curva molto stretta (“grande
curvatura”), la circonferenza che meglio la approssima è molto
piccola, ossia ha un raggio piccolo.
Al contrario se la curva è molto larga (“piccola curvatura”), la
circonferenza che meglio la descrive avrà un raggio molto grande.
Dato che è possibile disegnare una curva per ogni punto di un
percorso qualsiasi, le circonferenze sono infinite.
4) calcolo del campo elettrostatico generato da una lastra piana uniformemente carica.
Fino ad ora abbiamo studiato i campi elettrici generati da singole cariche. Prendiamo ora in
considerazione un campo generato non più da una carica, ma da una lastra uniformemente
carica.
La prima immagine mostra la
lastra ed alcuni suoi vettori
campo. (fig. 1)
Immaginiamo ora la lastra
vista di profilo, e prendiamo
in considerazione un vettore
campo qualsiasi. Attorno a
questo vettore disegniamo
una superficie cilindrica,
come in fig. 2.
(fig. 1)
(fig. 2)
www.easymaths.altervista.org
Calcoliamo ora il flusso utilizzando separatamente le due formule note:

Utilizziamo  s ( E )  E  S  cos( )
Il flusso totale è dato dalla somma del flusso delle basi con quello della superficie laterale:



 cilindro ( E )   basi ( E )   lati ( E )

Il flusso delle basi è  basi ( E )  2  E  A  1  2  E  A
Dove:
2 perché le basi sono due
A area della base
cos(0) = 1 l’angolo tra il versore e il vettore campo è 0
Il flusso della superficie laterale è 0 poiché l’angolo tra il
versore e il vettore campo in questo caso sarebbe 90, il cui
coseno è 0 che annulla la formula.

Quindi  cilindro ( E )  2  E  A

Q
Utilizziamo  S ( E ) 
0
Dato che questa formula dipende solo dalle cariche e dalla costante dielettrica, possiamo
scrivere subito la formula del flusso nel cilindro:

Q
 cilindro ( E ) 
0
Q
Q
Dato che    Q    A possiamo
A
0
scrivere la formula effettuando le opportune semplificazioni:
Uniamo le formule del flusso ottenute: 2  E  A 

A
 E
20
0
Abbiamo così ottenuto la formula del campo elettrostatico in una lastra uniformemente carica.
Questa formula vale solo nelle situazioni vicine alla lastra.
2E  A 
www.easymaths.altervista.org
N.B. Analizziamo la situazione in cui vi siano due lastre di carica opposta, l’una di fronte all’altra
come in figura. (Si suppone che le due lastre abbiano la stessa densità di carica)
Dato che vale il principio di sovrapposizione, è facile notare come nell’area compresa tra le due
lastre i vettori campo si sommino, mentre all’esterno si annullino. (Ricordiamo che i vettori
rappresentanti un campo si disegnano entranti se le cariche sono negative, uscenti se sono positive).
Il campo totale è dato dalla somma algebrica dei due campi. E tot 
www.easymaths.altervista.org





20 20 0
Piano di cariche
E
La simmetria dello spazio è
piana.
S
E
S
S
E
Scegliamo come superficie
gaussiana una superficie cilindrica
con asse perpendicolare al piano
Il vettore E è perpendicolare
al piano di cariche di densità
superficiale sigma e quindi il
flusso di E attraverso ogni
piano di base del cilindro è
E*S
mentre è nullo
attraverso la superficie
laterale
Q S

 S ( E )  2 ES 

E
0 0
2 0
www.easymaths.altervista.org
Linea retta di cariche
La simmetria è
cilindrica
S
La superficie gaussiana
è un cilindro con asse la
linea di carica.
E
S
E
Il campo E ha direzione
perpendicolare alla linea
di cariche
Il flusso attraverso le basi
è nullo.
Il flusso totale è quello
attraverso la superficie
laterale.
Q  *l

 S ( E )  E * 2r * l 

E
0
0
2 0 r
www.easymaths.altervista.org
Sfera piena di cariche
La simmetria è sferica.
R

r
La superficie gaussiana è una
superficie sferica concentrica
di raggio r.
Q
4 3
R
3
Il campo elettrico all’interno della
sfera è proporzionale ad r. Per r=R
si riottiene l’espressione del
campo elettrico di una carica Q.
q
q
S (E)  E * 4r   E 
0
40r 2
2
Q 4 3
r
4
4 33
 r 3
R
Q
3
3
E 


r
2
2
3
40r
40r
40 R
E
R
r
Se faccio un buco lungo tutto il diametro di una sfera carica positivamente,
quale sarà il moto di una carica negativa lasciata ad una uscita del buco?
www.easymaths.altervista.org
Superficie sferica conduttrice carica
La simmetria è sferica.
R
La superficie gaussiana è una
sfera.
r
il raggio
della
Se Se
il raggio
della
superficie
superficie
gaussiana è r<R
gaussiana
è r>R
r
2
E
q  0   S ( E )  4r E  0  E  0
Q
1 Q
 S ( E )  4r E   E 
0
4 0 r 2
2
www.easymaths.altervista.org
r
Condensatore piano carico
Un condensatore è costituito da due
armature metalliche piane e parallele.
La simmetria è piana
S
E
Prendiamo come superficie
gaussiana un cilindro con
una base parallela esterna
all’armatura e una base
interna.
Il flusso del campo è nullo
attraverso la base nell’armatura
e attraverso la superficie
laterale.
Il flusso totale è dato da
quello del campo elettrico
attraverso la base posta tra le
armature.
Q S

 S (E)  E * S 

E
0 0
0
www.easymaths.altervista.org