TEOREMA DI GAUSS
Il flusso del campo elettrico attraverso una superficie chiusa è
uguale alla somma delle cariche racchiuse diviso la costante
dielettrica.
Φ S (E) =
∑
Q
ε0
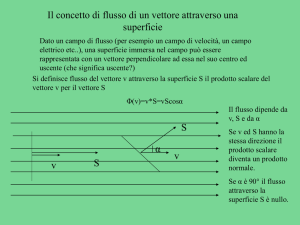
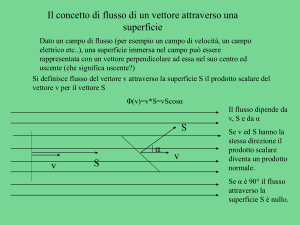
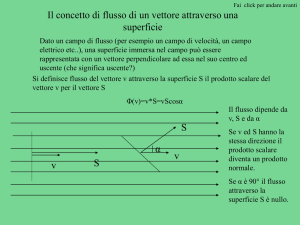
Flusso di un vettore
Si consideri una superficie qualsiasi,
per il momento piana, all’interno di un
campo per il momento uniforme. Si
tracci la perpendicolare (n) alla
superficie e la si orienti. Sia α l’angolo
che il vettore forma con la normale alla
superficie. Il flusso di un vettore
attraverso la superficie è definito dall'
espressione: dove S è l’area della superficie.
Nella rappresentazione del campo mediante
linee di forza, si può immaginare il flusso
come il numero di linee che attraversano la
superficie S.
Il flusso è:
• nullo quando α =90° (linee di forza parallele
alla superficie);
•massimo positivo quandoα =0 linee di forza
perpendicolari alla superficie e concordi con
la normale;
•massimo negativo se la normale orientata
forma con le linee di forza un angolo di 180°.
Se il campo non è uniforme e se la superficie non è piana
si può pensare di suddividere la superficie stessa in n
porzioni ed eseguire per ognuna di queste parti il calcolo
del flusso come precedentemente descritto. Il flusso
attraverso la superficie S è allora dato dall’espressione:
dove Ai è il modulo del vettore rappresentativo del
campo per i punti delle superficie Si ed α i è l’angolo
che la normale a questa superficie forma con il vettore
Ai .
Carica puntiforme
E
E
La simmetria dello spazio è
sferica.
S2
S1
E
Scegliamo come superficie
gaussiana una sfera di centro la
carica Q
Dividiamo la superficie della
sfera in porzioni
rappresentati dai vettori
S1,S2…..Per simmetria il
campo elettrico E è costante
sull’intera superficie.
Q
E
Si ha:
Φ S ( E ) = ES1 + ES 2 + .... + ES n = E ( S1 + S 2 + .. + S n ) = E 4π r 2 =
Q
1 Q
⇒ E=
ε0
4π ε 0 r 2
Piano di cariche
E
La simmetria dello spazio è
piana.
S
E
S
E
S
Scegliamo come superficie
gaussiana una superficie cilindrica
con asse perpendicolare al piano
Il vettore E è perpendicolare
al piano di cariche di densità
superficiale sigma e quindi il
flusso di E attraverso ogni
piano di base del cilindro è
E*S
mentre è nullo
attraverso la superficie
laterale
Q σS
σ
Φ S ( E ) = 2 ES =
=
⇒ E=
ε0 ε0
2ε 0
Linea retta di cariche
La simmetria è
cilindrica
S
La superficie gaussiana è
un cilindro con asse la
linea di carica.
E
S
E
Il campo E ha direzione
perpendicolare alla linea
di cariche
Il flusso attraverso le basi
è nullo.
Il flusso totale è quello
attraverso la superficie
laterale.
Q λ *l
λ
Φ S ( E ) = E * 2π r * l =
=
⇒ E=
ε0
ε0
2π ε 0 r
Sfera piena di cariche
La simmetria è sferica.
R
r
ρ =
La superficie gaussiana è una
superficie sferica concentrica
di raggio r.
Q
4 3
πR
3
Il campo elettrico all’interno della
sfera è proporzionale ad r. Per r=R
si riottiene l’espressione del
campo elettrico di una carica Q.
q
q
Φ S ( E ) = E * 4π r =
⇒ E=
ε0
4π ε 0 r 2
2
Q 4 3
πr
4 3 4 33
ρ πr
πR
Q
3
3
⇒ E=
=
=
r
2
2
3
4π ε 0 r
4π ε 0 r
4π ε 0 R
E
R
r
Superficie sferica conduttrice
carica
La simmetria è sferica.
R
La superficie gaussiana è una
sfera.
Se il raggio della superficie
gaussiana è r>R
r
Se il raggio della
superficie gaussiana è r<R
E
q = 0 ⇒ Φ S ( E ) = 4π r 2 E = 0 ⇒ E = 0
Q
1 Q
Φ S ( E ) = 4π r E =
⇒ E=
ε0
4π ε 0 r 2
2
r
Condensatore piano carico
Un condensatore è costituito da due
armature metalliche piane e parallele.
La simmetria è piana
S
E
Prendiamo come superficie
gaussiana un cilindro con
una base parallela esterna
all’armatura e una base
interna.
Il flusso del campo è nullo
attraverso la base nell’armatura e
attraverso la superficie laterale.
Il flusso totale è dato da
quello del campo elettrico
attraverso la base posta tra le
armature.
Q σS
σ
Φ S (E) = E * S =
=
⇒ E=
ε0 ε0
ε0