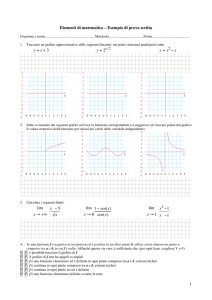
Studio di funzioni
Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle
seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si
indichino esplicitamente eventuali massimi o minimi assoluti.
1. f(x) = x4 – 2x3
2. f(x) =
x
(1 + x )2
3. f(x) = e
1
x
4. f(x) = xex
5. f(x) = x2ex
6. f(x) = x ln(x)
Soluzioni
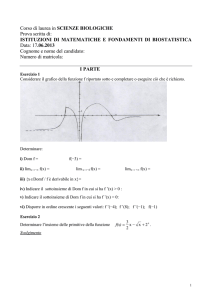
1. Per prima cosa determiniamo il dominio della funzione. Poiché abbiamo a che fare
esclusivamente con somme di funzioni potenza (non c’è pericolo che si divida per zero o
che si stia facendo il logaritmo di un numero minore o uguale a zero, o la radice quadrata
di un numero negativo, ecc.), evidentemente il dominio della funzione è (-∞,+∞).
Il secondo passo è determinare (se, a seconda dei calcoli, questo è possibile) gli intervalli
in cui f(x) >0 e, quindi, gli intervalli dove la funzione è negativa. La funzione f(x) risulta
positiva se e solo se x4 – 2x3 > 0, cioè, mettendo in evidenza x3,
x3(x – 2) > 0
Quindi la funzione è positiva quando il prodotto delle due quantità x3 e x – 2 è positivo,
cioè quando questi due fattori hanno lo stesso segno (ricorda che “+ per + è +, e – per – è
+”). Studiamo dunque separatamente il segno dei due fattori x3 e x – 2. Si noti che x3 =
x2⋅x e quindi (essendo x2 sempre maggiore o uguale a 0) x3 > 0 se e solo se x > 0. Invece
l’altro fattore, x – 2, è maggiore di 0 se e solo se x > 2. Per confrontare i segni dei due
fattori, rappresentiamo graficamente la situazione:
x3 > 0
x–2>0
0
--------------------------------————————————————————
+
–
+
--------------------------------------------------——————————————
2
Dal confronto dei segni dei due fattori, segue che il loro prodotto è positivo per x < 0
oppure per x > 2. Quindi f(x) > 0 negli intervalli (− ∞,0 ) e (2,+∞ ) .
Riportiamo, per nostra convenienza, sia il dominio sia la positività della funzione, su due
linee, una sotto l’altra:
D: ————————————————————————
f(x)>0: ———————○----------------------○-————————
0
2
Può essere comodo avere a disposizione qualche punto che appartiene al grafico della
funzione. Tali punti possono essere ottenuti, per esempio, trovando le intersezioni con
gli assi. Le intersezioni con l’asse x (y = 0) sono tutti i punti le cui ascisse soddisfano
l’equazione
x4 – 2x3 = 0
cioè x = 0 e x = 2. Quindi i punti di coordinate (0,0) e (2,0) appartengono al grafico della
funzione. Per ottenere le intersezioni con l’asse y, dobbiamo invece sostituire x = 0 a y =
x4 – 2x3. Si ottiene che necessariamente x = 0 e quindi l’unica intersezione con l’asse y è il
punto (0,0), punto che avevamo già trovato.
Procediamo nel nostro studio calcolando i limiti della funzione negli estremi del
dominio, anche al fine di trovare eventuali asintoti orizzontali e verticali1. Dato che D =
(− ∞,+∞ ) , dobbiamo calcolare lim f (x ) e lim f (x ) . Si ha che:
x → +∞
1
x → −∞
Prescinderemo, sia per ragioni di tempo che per coerenza con i libri di testo consigliati, dalla ricerca di eventuali asintoti
obliqui.
2
lim f (x ) = lim x 4 − 2 x 3 = lim x 4 1 − = +∞
x → +∞
x → +∞
x
(
x → +∞
)
dato che 2/x tende a 0.
Per x che tende a -∞ non vi è invece alcuna forma indeterminata e concludiamo
direttamente che
(
)
lim f (x ) = lim x 4 − 2x 3 = +∞ .
x → −∞
x → −∞
Non vi è quindi alcun asintoto orizzontale (e nemmeno verticale, chiaramente), ma in ogni
caso il risultato dei limiti ci dice che per valori di x (positivi o negativi) via via sempre più
grandi in valore assoluto la funzione tende ad assumere valori positivi via via sempre più
grandi. Ciò è in accordo anche con lo studio della positività della funzione (che, appunto,
risultava positiva agli estremi del dominio).
A questo punto calcoliamo la derivata della funzione e ottenendo che
f’(x) = 4x3 – 6x2.
Al fine di determinare gli intervalli dove la funzione è crescente o decrescente e quindi gli
eventuali punti di massimo, minimo o flesso a tangente orizzontale, studiamo la
disequazione f’(x) > 0, cioè
2x2 (2x – 3) > 0.
3
. Rappresentiamo graficamente la situazione
2
evidenziando con delle frecce le zone dove la funzione è crescente o decrescente:
Tale disequazione è verificata per x >
3
0
2
f’(x) > 0: ----------------○----------------○-—————————————
3
3
Pertanto la funzione è decrescente nell’intervallo − ∞, e crescente in ,+∞ . Nei
2
2
3
3
punti x = 0 e x =
la derivata si annulla: f ′(0 ) = 0 , f ′ = 0 . Dato che la funzione è
2
2
decrescente sia a sinistra che a destra di x = 0, si ha che x = 0 è un punto di flesso a
tangente orizzontale. Tale flesso ha quindi coordinate (0,f(0)) = (0,0). Invece, come si
3
vede chiaramente anche dalla rappresentazione grafica in alto, x =
è un punto di
2
4
3
81
27
27
3 3
3
minimo relativo. In tale punto la funzione vale f = − 2 =
,
−2
=−
2
2
2
16
8
16
3 27
cioè circa 1,69. Quindi il minimo m ha coordinate ,−
.
2 16
Man mano che acquisiamo tutte queste informazioni, è bene cominciare a rappresentarle
nella bozza di grafico (quindi, per esempio, si possono segnare le intersezioni con gli assi,
il massimo relativo, il flesso a tangente orizzontale, ecc.).
Concludiamo con lo studio del segno della derivata seconda, al fine di determinare gli
intervalli dove la concavità della funzione è rivolta verso l’alto o verso il basso, ed eventuali
altri punti di flesso. Effettuiamo quindi la derivata di f’(x) = 4x3 – 6x2, ottenendo
f’’(x) = 12x2 – 12x = 12x (x – 1).
Studiamo dunque la disequazione f’’(x) > 0. Si tratta di una disequazione di secondo
grado, che è verificata negli intervalli esterni rispetto ai valori x = 0 e x = 1
f’’(x)>0: ———————○----------------------○-————————
0
1
Pertanto la funzione ha la concavità rivolta verso l’alto negli intervalli (− ∞,0 ) e (1,+∞ ) ,
mentre ha la concavità rivolta verso il basso nell’intervallo (0,1). Rappresentiamo questo
graficamente con degli “archetti”. Nei punti x = 0 e x = 1 la concavità subisce un
cambiamento e la derivata seconda si annulla, cioè f’’(0) = 0 e f’’(1) = 0. Concludiamo
quindi che x = 0 e x =1 sono punti di flesso. Notiamo peraltro che il flesso in x = 0 era stato
già determinato precedentemente, con lo studio della crescenza / decrescenza della
funzione; concentriamoci quindi sul secondo punto di flesso, quello in x = 1. In tale punto
la funzione assume valore f(1) = 14 – 2·13 = –1. Quindi, oltre al flesso F1(0,0), già trovato
prima, abbiamo trovato anche il flesso F2(1,–1). In tali punti, lo ricordiamo, la concavità
della funzione cambia.
A questo punto cerchiamo di “tirare le somme” su tutte le informazioni sin qui ottenute e
abbozziamo uno schizzo di grafico. Può anche essere utile dare alla x valori arbitrari e
ottenere i corrispondenti valori di y = x4 – 2x3, onde ottenere ulteriori punti per i quali il
grafico passa.
Nel cominciare a disegnare si può per esempio partire a sinistra del foglio, cioè quando x
tende a -∞. Qui abbiamo visto che la funzione tendeva a +∞, quindi dobbiamo cominciare
a disegnare dall’angolo superiore sinistro del foglio. Sappiamo che la funzione è
decrescente fino a x = 3/2 e che ha la concavità verso l’alto fino a x = 0 (punto di flesso a
tangente verticale), e quindi con la penna scendiamo sino a x = 0, dove la funzione vale 0
(informazione che avevamo ottenuto quando abbiamo trovato le intersezioni con gli assi).
In x = 0 la concavità cambia ma la funzione rimane decrescente. La concavità cambia
nuovamente nell’altro flesso F2(1,–1). La funzione rimane decrescente fino al minimo m
3 27
,−
. Dopo tale minimo, la funzione sale intersecando l’asse delle x in x = 2 e,
2 16
mantenendo la concavità rivolta verso l’alto, tende a +∞ man mano che x tende a +∞.
Il disegno così ottenuto dovrebbe essere simile a quello in basso:
F1
F2
m
Infine, quanto ai massimi e minimi assoluti, notiamo che la funzione non ha massimi
3 27
assoluti (infatti tende a +∞), mentre l’unico minimo relativo m ,−
è anche minimo
2 16
assoluto: come ben si vede dal grafico, tale punto è il punto di ordinata più “bassa” di tutto
il grafico.
x
è quella funzione che ad un numero x associa il numero x
(1 + x )2
diviso per (1 + x)2. Poiché, come è noto, è vietato dividere per zero (!), dobbiamo
assicurarci, appunto, di non dividere per zero e quindi dobbiamo imporre che
2. La funzione f(x) =
(1 + x)2 ≠ 0,
cioè 1 + x ≠ 0, cioè x ≠ –1. Quindi il dominio D è costituito da tutta la retta reale con
l’esclusione del punto –1. Quindi, D = (–∞,–1) ∪ (–1,+∞).
Intersezione con gli assi. Cominciamo con l’intersezione con l’asse delle x (cioè la retta di
equazione y = 0). Dobbiamo risolvere il sistema
x
y =
(1 + x )2
y = 0
x
= 0 , che è verificata se e solo se il numeratore si annulla (e,
(1 + x )2
naturalmente, il denominatore è diverso da 0), cioè quando x = 0. Quindi il grafico della
funzione interseca l’asse x unicamente nel punto (0,0). Per quanto riguarda le intersezioni
con l’asse delle y (cioè la retta di equazione x = 0), risolviamo il sistema
Otteniamo quindi che
x
y =
(1 + x )2
x = 0
che, sostituendo x = 0 nella prima equazione, ci dà anche in questo caso come unica
soluzione il punto (0,0).
x
, dobbiamo studiare il segno di
Per studiare la positività della funzione f(x) =
(1 + x )2
numeratore e denominatore. Il numeratore è evidentemente positivo se x > 0, mentre il
denominatore, essendo il quadrato di qualcosa, è sempre positivo tranne quando è 0, cioè
quando x = –1:
0
x > 0: ─────────────────○▬▬▬▬▬▬▬
–
–
+
(1 + x)2 > 0: ▬▬▬▬▬▬▬○▬▬▬▬▬▬▬▬▬▬▬▬
–1
Poiché stiamo cercando i valori della variabile x per i quali f(x) > 0, dobbiamo prendere in
considerazione le zone (contrassegnate con il “+”) dove numeratore e denominatore
hanno lo stesso segno (cosicché, appunto, il risultato della divisione avrà segno positivo).
Quindi la funzione sarà positiva (cioè il suo grafico giace al di sopra dell’asse delle x) per x
> 0. Rappresentiamo nella figura in basso il dominio e la positività della funzione sulla retta
reale:
–1
D: ▬▬▬▬▬▬▬○▬▬▬▬▬▬▬▬▬▬▬▬
f(x) > 0: ─────────────────○▬▬▬▬▬▬▬
0
Con le freccette blu abbiamo indicato graficamente tutti i limiti che dobbiamo calcolare, in
corrispondenza degli estremi del dominio. In totale 4: a +∞ e –∞, e poi a –1 da sinistra e
da destra.
lim
x → +∞
x
∞
=
2
(1 + x ) ∞
Si tratta di una forma indeterminata che si può risolvere applicando il teorema de l’Hôpital:
lim
x → +∞
x
1
= lim
= 0,
2
x
→
+∞
2
x
+2
(1 + x )
poiché il numeratore è un numero, mentre il denominatore tende, nel suo complesso, a
+∞. Analogamente, nello stesso modo, si vede che
lim
x → −∞
x
1
= lim
= 0.
2
x
→
−∞
2
x
+2
(1 + x )
Dunque la funzione ammette un asintoto orizzontale: la retta y = 0. Inoltre,
lim−
x → −1
x
= −∞
(1 + x )2
in quanto il numeratore tende a –1 (da sinistra), quindi è un numero negativo, mentre il
denominatore è un numero comunque positivo (è il quadrato di 1+x) che tende a 0. Si noti
che tale risultato è coerente con lo studio della positività di f(x), dato che la funzione risulta
negativa a sinistra di 0. Ragionando allo stesso modo si ha che
lim+
x → −1
x
= −∞ .
(1 + x )2
La retta x = –1 è un asintoto verticale. Il grafico “provvisorio” della funzione è quindi il
seguente, tenendo conto delle informazioni che finora abbiamo trovato: dominio, positività,
intersezioni con gli assi, asintoti orizzontali e verticali.
y
●
-1
x
Calcoliamo ora la derivata della funzione.
2
f ′(x ) =
1⋅ (1 + x ) − x ⋅ 2(1 + x ) (1 + x )(1 + x − 2 x )
1− x
=
=
.
4
4
(1 + x )
(1 + x )
(1 + x )3
Studiamo quando f ′(x ) > 0 . Studiamo quindi il segno di numeratore e denominatore. Per
quanto riguarda il numeratore, si noti che 1 – x > 0 se x – 1 < 0, cioè x < 1. Invece,
riguardo al denominatore, si ha che (1 + x)3 = (1 + x)2(1 + x) > 0 se e solo se 1 + x > 0,
cioè x > –1. Riassumendo
1
1– x > 0: ▬▬▬▬▬▬▬▬▬▬▬▬○──────────
–
+
–
3
(1 + x) > 0: ──────────○▬▬▬▬▬▬▬▬▬▬▬▬
–1
Quindi si ha che f ′(x ) > 0 se e solo se –1 < x < 1. Rappresentiamo graficamente il segno
della derivata sotto il dominio:
–1
D: ▬▬▬▬▬▬▬○▬▬▬▬▬▬▬▬▬▬▬▬
–1
1
f’(x) > 0: ──────────○▬▬▬▬▬○─────────
Se ne deduce che la funzione è decrescente nell’intervallo (–∞,–1), crescente
nell’intervallo (–1,1) e di nuovo decrescente in (1,+∞). Il punto di ascissa x = 1 risulta
essere un punto di massimo relativo. Erroneamente si potrebbe concludere che il punto di
ascissa x = –1 sia un punto di minimo relativo. Tuttavia x = –1 non appartiene al dominio e
quindi non ha nemmeno senso chiederci se tale valore sia un punto di minimo, perché in
tale punto la funzione non è proprio definita.
Calcolando il valore della funzione nel punto di ascissa 1, si ottiene quindi il massimo
1
M 1, .
4
Infine, per studiare la concavità della funzione, dobbiamo provare a calcolare la derivata
seconda, sperando che i calcoli non siano troppo complicati. Si ha che
′
1 − x − 1⋅ (1 + x )3 − (1 − x )3(1 + x )2 − (1 + x ) − 3(1 − x ) 2(x − 2 )
=
f ′′(x ) =
=
=
.
3
(1 + x )6
(1 + x )4
(1 + x )4
(1 + x )
Se ne conclude che f’’(x) > 0 se e solo se x – 2 > 0 cioè se e solo se x > 2.
Rappresentiamo graficamente il segno della derivata seconda sotto il dominio.
–1
D: ▬▬▬▬▬▬▬○▬▬▬▬▬▬▬▬▬▬▬▬
2
f’’(x) > 0: ────────────────────○▬▬▬▬▬
Quindi il grafico della funzione rivolge la concavità verso il basso nell’intervallo (–∞,2),
verso l’alto nell’intervallo (2,+∞). Il punto di ascissa x = 2, dove la concavità cambia e la
derivata seconda si annulla, è un flesso. Calcoliamo, al fine di rappresentarlo nel grafico, il
valore della funzione in questo punto: si ha che f(2) = 2/9. Quindi il flesso è il punto
2
F 2, .
9
Ora abbiamo tutte le informazioni per tracciare il grafico della funzione:
M
F
1
3. Per determinare il dominio di f(x) = e x dobbiamo innanzitutto capire quali sono le
funzioni coinvolte. Esse sono: la funzione esponenziale, che è definita su tutto R, e la
funzione che prende un numero x e restituisce 1/x. Quest’ultima operazione di divisione di
1 per x è consentita purché x sia diverso da zero (è severamente vietato dividere per
zero!). Quindi il dominio della funzione è dato da tutti i numeri reali eccetto 0: D = (–∞,0) ∪
(0,+∞).
Quanto al segno della funzione, si noti che la funzione risulta essere sempre strettamente
positiva, in quanto f(x) è sempre l’esponenziale di qualcosa (precisamente di 1/x) e come
tale è sempre positivo per qualsiasi valore di x.
Rappresentiamo come al solito graficamente, sulla retta reale, il dominio e la positività
della funzione:
0
D: ▬▬▬▬▬▬▬▬○▬▬▬▬▬▬▬▬▬
f(x) > 0: ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
Troviamo le intersezioni con gli assi. Non vi è alcuna intersezione con l’asse y dal
momento che il valore x = 0 è fuori dal dominio. D’altra parte le eventuali intersezioni con
l’asse x sono date dalle soluzioni del sistema
1
x
=
y
e
y = 0
che è equivalente all’equazione
1
ex = 0 .
Ma tale equazione non ha alcuna soluzione, in quanto la funzione esponenziale è sempre
strettamente positiva. Concludiamo che la nostra funzione non ha alcuna intersezione né
con l’asse x né con l’asse y.
Passiamo quindi a studiare il comportamento della funzione agli estremi del dominio.
Dobbiamo calcolare 4 limiti, uno per ciascuna delle freccette azzurre disegnate in alto.
Si ha che:
1
lim e x = 1,
x → +∞
in quanto 1/x → 0 per x che tende a +∞. Per lo stesso motivo si ha anche che
1
lim e x = 1.
x → −∞
Vi è quindi un asintoto orizzontale, e precisamente la retta di equazione y = 1.
Inoltre,
1
x
lim e = +∞
x →0 +
1
1
→ +∞ e quindi, a sua volta, e x → +∞ . Pertanto la
x
retta x = 0 è un asintoto verticale (destro), cioè il grafico della funzione si avvicinerà
sempre più alla retta x = 0 fino quasi ad apporgiarvisi dal lato destro. Invece
poiché quando x → 0 + la funzione
1
lim− e x = 0
x →0
1
1
dal momento che quando x → 0 la funzione
→ −∞ e quindi e x → 0 (tieni a mente il
x
grafico della funzione esponenziale). Ci aspettiamo quindi che la funzione quando si
avvicina a 0 da sinistra sia molto vicina al valore 0; in altre parole il grafico della funzione
“sfiora” l’origine (0,0). Di ciò dobbiamo tenere conto quando disegneremo il grafico.
−
Passiamo ora al calcolo della derivata, in modo da studiare la crescenza e decrescenza
della funzione.
Si ha che
1
x
−1 ′
1
x
1
( ) = e (− 1⋅ x )
f ′(x ) = e ⋅ x
−1−1
ex
=− 2 .
x
1
ex
Di conseguenza, f’(x) > 0 se e solo se − 2 > 0 , che è equivalente a risolvere
x
1
ex
<0.
x2
Si noti che tale disequazione non è mai verificata. Infatti il numeratore è sempre positivo
(lo abbiamo visto prima, l’esponenziale di qualcosa è sempre un numero positivo) ed
anche il denominatore è sempre positivo tranne che in 0 (punto che però è escluso dal
1
ex
dominio). Quindi 2 è il rapporto tra due numeri positivi e quindi è a sua volta un numero
x
positivo.
Graficamente quindi il segno della derivata è rappresentato da una linea continua in cui
non vi alcun tratto “calcato”:
0
f’(x) > 0: ──────────────○─────────────
La funzione quindi risulta essere sempre decrescente, in tutti i punti del suo dominio.
Dato che l’espressione della derivata non appare particolarmente complicata, proviamo a
calcolare la derivata seconda:
1
1
′
1
1
1 x 2
x
−
e
⋅
x
−
e
⋅ 2 x e x (2x + 1)
2
ex
f ′′ = − 2 = − x
=
.
x4
x4
x
1
Di conseguenza f ′′(x ) > 0 se e solo se 2x + 1 > 0, cioè se e solo se x > − :
2
0
D: ▬▬▬▬▬▬▬▬▬○▬▬▬▬▬▬▬▬
–1/2
f ′′( x ) > 0 : ───────○▬▬▬○▬▬▬▬▬▬▬▬
Pertanto il grafico della funzione ha la concavità rivolta verso il basso nell’intervallo
1
1
− ∞,− e verso l’alto in − ,0 e (0,+∞ ) (chiaramente abbiamo escluso il valore x = 0
2
2
1
in quanto non appartiene al dominio). Nel punto di ascissa x = − la concavità cambia e
2
la derivata seconda si annulla … esso è quindi un punto di flesso. L’ordinata è pari a
1
1
1 1
f − = e − 2 = 2 . Quindi la funzione ammette il flesso F − , 2 .
e
2
2 e
Abbiamo quindi tutte le informazioni per disegnare il grafico della funzione, che è
approssimativamente il seguente:
F
4. Il dominio della funzione f(x) = xex è evidentemente tutta la retta reale, dal momento che
la funzione esponenziale è definita su tutto R, come pure la funzione y = x.
D: ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
Gli intervalli dove la funzione è positiva si trovano risolvendo la disequazione
x·ex > 0.
Per risolverla dobbiamo studiare separatamente il segno di ciascuno dei due fattori, x ed
ex, e poi confrontare il loro segno tenendo conto della ben nota regola dei segni (una
quantità positiva moltiplicata per una negativa dà una quantità negativa, una positiva per
una positiva dà una quantità positiva, ecc.).
0
───────────○▬▬▬▬▬▬▬▬
–
+
ex > 0 ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
x>0
Dato che stiamo cercando le zone dove la quantità x·ex è positiva, dobbiamo prendere in
considerazione gli intervalli contrassegnati dal “+”. In definitiva x·ex > 0 per x appartenente
all’intervallo (0,+∞).
D: ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
f(x) > 0: ────────────○▬▬▬▬▬▬▬▬
0
Procediamo a determinare le intersezioni con gli assi cartesiani. Le intersezioni con l’asse
x sono tutte le soluzioni dell’equazione
x·ex = 0.
Si noti che tale equazione ammette l’unica soluzione x = 0 dal momento che l’altro fattore,
ex, è una quantità sempre strettamente diversa da zero (positiva, per la precisione). Quindi
l’origine O(0,0) è l’unica intersezione della funzione con l’asse x. Le intersezioni con l’asse
y sono date dai punti di ascissa 0 e ordinata y = 0·e0 = 0. In definitiva anche in questo
caso l’unica intersezione trovata è l’origine.
Possiamo ora cominciare a studiare il comportamento della funzione agli estremi del
dominio, cioè a +∞ e –∞.
D: ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
lim xe x = +∞ ,
x → +∞
poiché sia la funzione y = x che y = ex tendono a +∞ quando x → +∞. Invece
lim xe x = 0 .
x → −∞
La ragione di questo risultato è la seguente. Quando x → –∞ la funzione y = x tende a –∞,
mentre la funzione y = ex tende a 0. Abbiamo quindi una forma indeterminata del tipo 0·∞.
Tuttavia è sufficiente notare che ex tende a 0 più rapidamente di quanto x tenda a –∞ … in
pratica tra le due funzioni (x ed ex) quella che “vince” è ex.
Un modo più classico di risoluzione può essere quello di utilizzare la regola de l’Hôpital.
Come noto, il teorema di de l’Hôpital si può però utilizzare solo per risolvere le forme
indeterminate 0/0 oppure ∞/∞. Di conseguenza riscriviamo il nostro limite in questo modo
lim xe x = lim
x → −∞
x → −∞
x
.
e− x
Abbiamo così trasformato la forma indeterminata 0·∞ in una forma indeterminata
∞
. Ora
∞
sì che possiamo applicare la regola di de l’Hôpital! Si ha:
lim xe x = lim
x → −∞
x → −∞
x
( x )′
1
= lim − x = lim
= 0.
−x
x
→
−∞
x
→
−∞
e
(e )′
− e− x
L’ultimo passaggio si spiega col fatto che il numeratore è un numero (il numero 1), mentre
il denominatore è una quantità che tende a –∞ per x → –∞.
Pertanto vi è un asintoto orizzontale, la retta y = 0.
Calcoliamo la derivata:
f ′(x ) = 1⋅ e x + x ⋅ e x = e x (1 + x ) .
Non dovresti avere difficoltà a concludere che f’(x) > 0 se e solo se x > –1.
–1
′
f ( x ) > 0 : ───────────○▬▬▬▬▬▬▬▬▬
Pertanto la funzione è decrescente nell’intervallo (–∞,–1) e crescente in (–1, +∞), e in –1 vi
è un minimo. Dato che f(–1) = –e–1 = –1/e, il minimo m avrà coordinate (–1,–1/e).
Procediamo con il calcolo della derivata seconda, dato che i calcoli appaiono piuttosto
agevoli:
f ′′(x ) = e x ⋅ (1 + x ) + e x ⋅ 1 = e x (2 + x ) .
Di conseguenza f’’(x) > 0 se e solo se 2 + x > 0, cioè se e solo se x > –2:
–2
f ′′( x ) > 0 : ──────────○▬▬▬▬▬▬▬▬
Otteniamo dunque un’altra informazione e cioè che il grafico della funzione avrà la
concavità rivolta verso il basso nell’intervallo (–∞,–2) e verso l’altro in (–2,+∞). In –2
2
abbiamo un flesso. Per trovarne l’ordinata calcoliamo f(–2) = –2e–2 = − 2 . Quindi il nostro
e
2
flesso sarà il punto F − 2,− 2 , che ci segniamo sugli assi cartesiani.
e
Abbiamo dunque tutti gli strumenti per disegnare uno schizzo del grafico, che è
rappresentato dalla figura in basso:
F
m
5. Esattamente come nell’esercizio precedente, anche in questo caso il dominio (o campo
di esistenza) della funzione
f(x) = x2ex
è tutta la retta reale. Inoltre la funzione risulta essere sempre non-negativa, in quanto essa
è il prodotto di una quantità sempre non negativa (x2) con una sempre strettamente
positiva (ex).
L’unica intersezione del grafico della funzione tanto con l’asse x quanto con l’asse y è data
dall’origine O(0,0).
D: ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
f(x) > 0: ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
Passiamo a studiare il comportamento della funzione agli estremi del dominio, al fine di
trovare eventuali asintoti. Cominciamo con +∞:
lim x 2e x = +∞
x → +∞
dal momento che entrambi i fattori, x2 ed ex, tendono a +∞ quando x tende a +∞. Inoltre
lim x 2e x = 0 .
x → −∞
Infatti, anche in questo caso vi è una forma indeterminata del tipo ∞·0, che può essere
risolta esattamente come nell’esercizio precedente, cioè utilizzando la regola di de
l’Hôpital oppure osservando che, quando x → –∞, ex tende a 0 più velocemente di quanto
x2 tenda a +∞. Il tutto ti viene lasciato come utile esercizio.
Quindi la retta y = 0 è un asintoto orizzontale.
Calcoliamo ora la derivata:
(
)
f ′( x ) = 2x ⋅ e x + x 2 ⋅ e x = x 2 + 2 x e x .
Dato che ex è una quantità sempre positiva, abbiamo che f’(x) > 0 se e solo se x2 + 2x > 0.
Tale disequazione è verificata per valori esterni a –2 e 0. Quindi, ricapitolando, f’(x) > 0
quando x < –2 oppure x > 0:
–2
0
′
f ( x ) > 0 : ▬▬▬▬▬▬▬○─────────○▬▬▬▬▬▬▬
Pertanto la funzione risulta essere crescente negli intervalli (–∞, –2) e (0, +∞), e
decrescente nell’intervallo (–2, 0).
In x = 0 vi sarà un minimo relativo, mentre in x = –2 un massimo relativo. Dato che f(0) = 0
e f(–2) = (–2)2e–2 = 4/e2, il minimo sarà dato dal punto m(0,0), cioè l’origine degli assi,
mentre il massimo dal punto M(–2,4/e2). Può essere utile già disegnare questi due punti su
un sistema di assi cartesiani.
Infine, la derivata seconda è data da
f ′′( x ) = (2 x + 2)e x + ( x 2 + 2 x )e x = ( x 2 + 4 x + 2)e x
e quindi f ′′( x ) > 0 se e solo se x 2 + 4 x + 2 > 0 . Risolviamo quest’ultima disequazione. Le
soluzioni dell’equazione di secondo grado associata sono
x=
− 4 ± 16 − 8 − 4 ± 8
=
= −2 ± 2 ,
2
2
cioè x1 = −2 + 2 ≈ −0,59 e x2 = −2 − 2 ≈ −3,41. La disequazione è soddisfatta per valori
della x “esterni” rispetto ad x1 e x2:
x1
x2
′
′
f ( x ) > 0 : ▬▬▬▬▬▬▬○─────────○▬▬▬▬▬▬▬
Pertanto la funzione ammette 2 flessi: F1 nel punto di ascissa x1 = −2 + 2 ≈ −0,59 , per il
quale l’ordinata vale f(x1) ≈ 0,19, e F2 nel punto di ascissa x2 = −2 − 2 ≈ −3,41, per il
quale l’ordinata vale f(x2) ≈ 0,38.
Tenuto conto di tutte le informazioni raccolte, il grafico della funzione è approssimativamente del tipo di quello disegnato nella figura in basso
M
F1
F2
m
6. La funzione f(x) = x ln(x) è definita dove è definita la funzione logaritmo. Cioè dobbiamo
imporre che x > 0. Il dominio è dunque D = (0,+∞).
Riguardo alle intersezioni con gli assi, ha senso solo trovare quella con l’asse x, perché
quella con l’asse y ci condurrebbe ad imporre x = 0, valore non appartenente al dominio.
Le eventuali intersezioni con l’asse x sono date dalle soluzioni del sistema
y = x ln( x )
y = 0
vale a dire dalle soluzioni dell’equazione
x ln(x) = 0.
Tale equazione è soddisfatta se e solo se x = 0 oppure ln(x) = 0. Le intersezioni quindi
sono date da x = 0 e x = 1.
Passiamo a studiare la positività / negatività della funzione, cioè trovare gli intervalli dove
la funzione è positiva e quelli dove è negativa. Dobbiamo sostanzialmente risolvere la
disequazione
x ln(x) > 0.
Studiamo quindi ciascuno dei due fattori, x e ln(x). Infatti la disequazione sarà soddisfatta
per quei valori della x per i quali i due fattori x e ln(x) hanno segno concorde. Tenuto conto
che ln(x) > 0 equivale a chiedere che ln(x) > ln(1), e quindi (dato che ln è una funzione
strettamente crescente!) x > 1, possiamo schematizzare il tutto nel modo seguente:
0
─────────○▬▬▬▬▬▬▬▬▬▬▬▬▬
+
–
+
ln(x) > 0 ───────────────────○▬▬▬▬▬▬
1
x>0
Siccome stiamo risolvendo la disequazione x ln(x) > 0, cioè stiamo cercando i valori di x
per i quali il prodotto di x e di ln(x) è positivo, dobbiamo scegliere le zone contrassegnate
dal simbolo “+”, che corrispondono proprio agli intervalli in cui x e ln(x) hanno segno
concorde. Si noti però che i valori a sinistra di 0 non appartengono al dominio e quindi
vanno esclusi.
In conclusione, la funzione è positiva per x > 1. In basso abbiamo rappresentato
schematicamente il dominio e la positività della funzione:
0
D: ──────○▬▬▬▬▬▬▬▬▬▬▬
f(x) > 0: - - - - - - -○──────○▬▬▬▬▬▬
0
1
Studiamo ora il comportamento agli estremi del dominio, cioè, in questo caso, a 0 (da
destra) e +∞.
Intanto si ha subito che
lim x ln( x ) = +∞
x → +∞
dal momento che sia x che ln(x) tendono a +∞ quando x → +∞. Quando invece x → 0+, il
limite
lim+ x ln( x )
x →0
dà luogo ad una forma indeterminata 0·(–∞). Trasformiamo tale forma indeterminata in
una del tipo ∞/∞, in modo da poter utilizzare la regola de l’Hôpital. È sufficiente scrivere il
limite in modo leggermente diverso:
1
′
ln x
ln x )
(
lim x ln( x ) = lim+
= lim x = lim+ − x = 0 .
= lim+
′ x →0 + 1
1
x →0 +
x →0
x →0
x →0
1
− 2
x
x
x
Quindi non ci sono asintoti orizzontali o verticali, ma la funzione in 0 “sfiora” il valore 0.
Cioè pur essendo l’origine degli assi un punto non appartenente al grafico della funzione
(perché 0 non appartiene al dominio), nelle sue immediate vicinanze la funzione “tende a
sfiorarlo”.
Il calcolo della derivata mostra che
f ′( x ) = 1⋅ ln( x ) + x ⋅
1
= ln( x ) + 1 .
x
Pertanto f’(x) > 0 se e solo se ln(x) > –1, cioè se e solo se e ln( x ) > e −1 , cioè x >
1
:
e
0
D: ──────○▬▬▬▬▬▬▬▬▬▬▬
f’(x) > 0: - - - -○──────○▬▬▬▬▬▬▬▬
1/e
Quindi la funzione è decrescente in (0, 1/e) e crescente in (0, +∞). In x = 1/e ≈ 0,37 vi è un
1
1 1 1
punto di minimo relativo, la cui ordinata è data da f = ln = − ≈ −0,37 .
e
e e e
In questo caso anche la derivata seconda è molto semplice ed è data semplicemente da
′ 1
f ′′( x ) = (1 + ln( x )) = .
x
Pertanto f’’(x) > 0 se e solo se x > 0. Questo risultato, tenendo conto che il dominio è
(0,+∞), ci dice che il grafico della funzione ha la concavità sempre rivolta verso l’alto:
0
D: ──────○▬▬▬▬▬▬▬▬▬▬▬
f’’(x) > 0: - - - - - - -○▬▬▬▬▬▬▬▬▬▬▬
0
Il grafico della funzione è rappresentato nella figura in basso.
m