AMPLIFICATORE OPERAZIONALE L`Amplificatore Operazionale

AMPLIFICATORE OPERAZIONALE
L’Amplificatore Operazionale (Operational Amplifier - OP) è un
dipositivo elettronico che si comporta come un generatore di
tensione controllsto in tensione
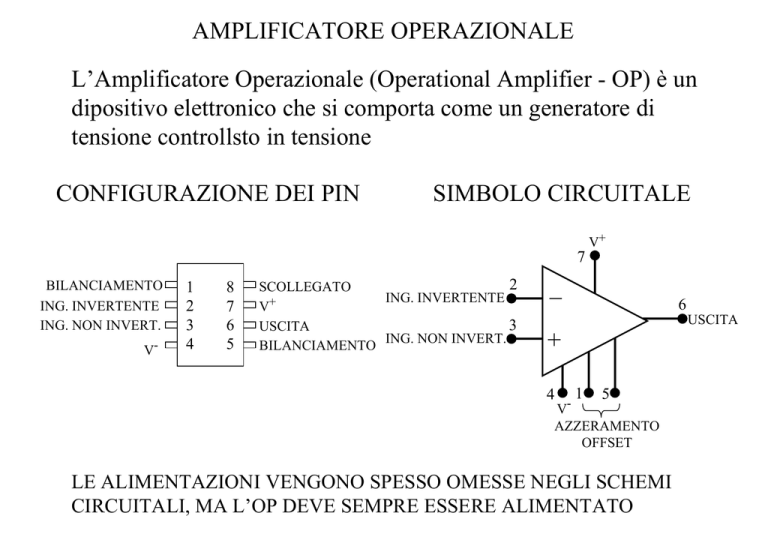
CONFIGURAZIONE DEI PIN
SIMBOLO CIRCUITALE
7
BILANCIAMENTO
ING. INVERTENTE
ING. NON INVERT.
V-
1
2
3
4
8
7
6
5
2
SCOLLEGATO
ING.
INVERTENTE
V+
3
USCITA
BILANCIAMENTO ING. NON INVERT.
V+
_
6
+
4 -1
V
5
AZZERAMENTO
OFFSET
LE ALIMENTAZIONI VENGONO SPESSO OMESSE NEGLI SCHEMI
CIRCUITALI, MA L’OP DEVE SEMPRE ESSERE ALIMENTATO
USCITA
MODELLO CIRCUITALE
v1
vd
v2
Ri
A·vd
Ro
Generatore di tensione
controllato in tensione
vo
vd = v2 −v1
vo = A ⋅ vd = A ⋅ (v2 −v1 )
A: guadagno di tensione ad anello aperto
valori tipici
A
105÷108
Ri
106÷1013 Ω
10÷100 Ω
Ro
5 ÷24 V tensione di
Vcc
alimentazione
vo
Vcc
saturazione positiva
vd
saturazione negativa
-Vcc
AMPLIFICATORE OPERAZIONALE IDEALE
i1 = 0
v1 i2 = 0
_
i1 = 0
vd
+
vo
v2 = v1
A=∞
i2 = 0

 Ri = ∞ ⇒
vd = v2 − v1 = 0
R = 0
 o
v2 = v1
NELLA MAGGIOR PARTE DELLE APPLICAZIONI SI CONSIDERANO OP
IDEALI NELLA REGIONE LINEARE DI FUNZIONAMENTO
NULLORE
i∞
i0
v0
0
∞
v∞
v0 = 0


 i0 = 0
v∞ qualsiasi


 i∞ qualsiasi
INSEGUITORE DI TENSIONE
Un generatore di tensione è collegato al morsetto
non invertente dell'operazionale, mentre il
morsetto invertente è collegato direttamente
all'uscita. Determinare la tensione in uscita vo
vo
vs
Ri ed Ro sono in serie. Quindi la corrente i vale:
i
vd
vs
Ri
A·vd
i=
Ro
vs − A ⋅ vd vs − A ⋅ Ri ⋅ i
=
Ri + Ro
Ri + Ro
per l'equilibrio delle tensioni alla maglia 1:
1
vo
vo = Ro ⋅ i + A ⋅ vd = Ro ⋅ i + A ⋅ Ri ⋅ i = (Ro + A ⋅ Ri ) ⋅ i
da cui, sostituendo:
vo
vs
A ⋅ Ri
vo
=
−
⋅
⇒
Ro + A ⋅ Ri Ri + Ro Ri + Ro Ro + A ⋅ Ri
vo
Ri + Ro + A ⋅ Ri
vs
⋅
=
⇒
Ro + A ⋅ Ri
Ri + Ro
Ri + Ro
vo =
Ro + A ⋅ Ri
⋅ vs ≈ vs
Ri + Ro + A ⋅ Ri
INSEGUITORE CON CARICO
i- = 0
vs
in
io
iL
vo
RL
Determinare il valore della corrente iL che attraversa
il carico RL
I due morsetti in ingresso all'operazionale hanno lo stesso potenziale. Il corto circuito
riporta lo stesso potenziale al morsetto di uscita, quindi vo = vs .
LA TENSIONE IN USCITA NON DIPENDE DAL CARICO
Per il calcolo della corrente:
vo
vs
iL =
=
RL RL
AMPLIFICATORE INVERTENTE
i1 R1
R2 i2
1
vs
Determinare il valore della tensione vo
2
in
io
vo
i1 = −i2
RL
ma, per l'idealità dell'operazionale:
da cui:
vs
v
=− o
R1
R2
e infine:
vo = −
equilibrio al nodo 1
i1 =
v s − v−
R1
equazione del componente R1
i2 =
vo − v−
R2
equazione del componente R2
v1 = v− = v+ = 0
R2
⋅ vs
R1
Questa configurazione di operazionale
amplifica l'ingresso in ragione del
rapporto R1/R2 e ne inverte il segno.
vs
t
vo
AMPLIFICATORE NON INVERTENTE
i1
R1
R2 i2
vs in
io
Determinare il valore della tensione vo
vo
RL
i1 = −i2
equilibrio al nodo 1
v−
i1 = −
R1
equazione del componente R1
i2 =
ma, per l'idealità dell'operazionale:
da cui:
−
vs
v −v
=− o s
R1
R2
e infine:
vo − v−
R2
equazione del componente R2
v− = v+ = v s
 R 
vo = 1 + 2  ⋅ vs
 R1 
t
Questa configurazione di operazionale
amplifica l'ingresso della quantità
1+R2/R1 e non inverte il segno.
vs
vo
AMPLIFICATORE SOMMATORE
i3 R3
i2 R2
v3
i1 R1
v2
v1
Determinare il valore della tensione vo
Ro i
in
io
vo
RL
i + i1 + i2 + i3 = 0
v
v
v
v
− o − 1 − 2 − 3 =0
Ro R1 R2 R3
da cui, riordinando
 v1 v2 v3 
vo = − Ro  +
+ 
 R1 R2 R3 
L'uscita è proporzionale alla somma pesata delle tensioni. Se R1 = R2 = R3 = R :
vo = −
Ro
(v1 + v2 + v3 )
R
Cioè l'uscita è proporzionale alla somma delle tensioni
AMPLIFICATORE DIFFERENZIALE
Determinare il valore della tensione vo
1 R2
R1
R1
v2
v1 R2
v+ = v1 ⋅
vo
RL
R2
= v− partitore di tensione
R1 + R2
v2 − v− vo − v− v2 vo R1 + R2
+
= +
−
⋅ v− = 0 equilibrio al nodo 1
R1
R2
R1 R2 R1 ⋅ R2
sostituendo:
R2
v2 vo R1 + R2
R2
+
−
⋅ v1 ⋅
= 0 ⇒ vo =
⋅ (v1 − v2 )
R1
R1 R2 R1 ⋅ R2
R1 + R2
Cioè l'uscita è proporzionale alla differenza tra le tensioni
AMPLIFICATORI ADINAMICI -TABELLA RIASSUNTIVA
inseguitore
di tensione
vo = vs
amplificatore
invertente
R2
vo = − ⋅ vs
R1
R2
amplificatore
non invertente
R2
R1
vs
vs
RL
vo
amplificatore
sommatore
R3
v3
vo
 v1 v2 v3 
vo = − Ro  +
+ 
 R1 R2 R3 
R2
RL
R1
v1
vo
RL
v2
vo
vo =
RL
R2
⋅ (v1 − v2 )
R1
R2
R1
R1
v2
vs
amplificatore
differenziale
Ro
 R 
vo = 1 + 2  ⋅ vs
 R1 
R1
v1 R2
vo
RL