IL PIANO CARTESIANO E LA RETTA
La distanza fra due punti
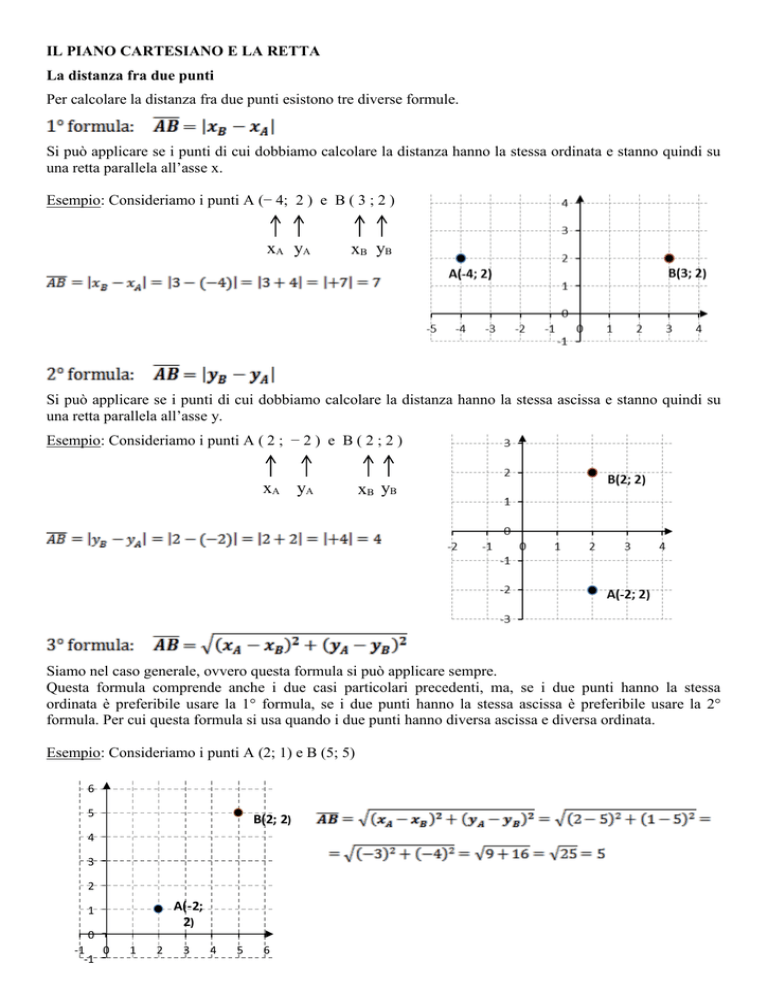
Per calcolare la distanza fra due punti esistono tre diverse formule.
Si può applicare se i punti di cui dobbiamo calcolare la distanza hanno la stessa ordinata e stanno quindi su
una retta parallela all’asse x.
Esempio: Consideriamo i punti A (− 4; 2 ) e B ( 3 ; 2 )
xA yA
xB yB
Si può applicare se i punti di cui dobbiamo calcolare la distanza hanno la stessa ascissa e stanno quindi su
una retta parallela all’asse y.
Esempio: Consideriamo i punti A ( 2 ; − 2 ) e B ( 2 ; 2 )
xA yA
xB yB
Siamo nel caso generale, ovvero questa formula si può applicare sempre.
Questa formula comprende anche i due casi particolari precedenti, ma, se i due punti hanno la stessa
ordinata è preferibile usare la 1° formula, se i due punti hanno la stessa ascissa è preferibile usare la 2°
formula. Per cui questa formula si usa quando i due punti hanno diversa ascissa e diversa ordinata.
Esempio: Consideriamo i punti A (2; 1) e B (5; 5)
6
5
B(2; 2)
4
3
2
A(-2;
2)
1
0
-1 0
-1
1
2
3
4
5
6
Il punto medio di un segmento
Il punto medio di un segmento AB è tale che
, cioè è quel punto che ha la stessa distanza dagli
estremi A e B del segmento.
Dati i punti
, il punto medio M del segmento AB ha le seguenti coordinate:
Esempio: Determiniamo il punto medio del segmento di estremi
Applicando la formula, abbiamo che:
.
L’equazione della retta nel piano cartesiano
Ogni retta del piano cartesiano è identificata da un’equazione.
4
y=3
3
2
1
Una retta parallela all’asse x, ha un equazione del tipo:
.
Esempio: Le rette in figura hanno equazione
-4
.
-3
-2
0
-1 0
-1
-2
-3
Una retta parallela all’asse y, ha un equazione del tipo:
Esempio: Le rette in figura hanno equazione
.
.
1
2
3
4
y=-2
Una retta passante per l’origine, diversa dall’asse y, ha equazione del tipo:
Esempio: Le retta in figura ha equazione
.
.
Ogni retta non parallela all’asse y ha equazione del tipo: y = mx + q dove m e q sono numeri reali.
Il significato dei coefficienti m e q
Nell’equazione della retta y = mx + q, il coefficiente m si chiama coefficiente angolare e il coefficiente q
termine noto. Per esempio, nell’equazione:
y = 2x + 3
Il coefficiente
angolare è 2
Il termine
noto è 3
Il termine noto q è l’ordinata del punto d’intersezione della retta di equazione y = mx + q con l’asse y.
6
4
2
(0; 2)
-> termine
noto q=2
0
-3
-1
1
3
-2
Il coefficiente angolare m dà invece informazioni sulla “inclinazione” della retta rispetto all’asse x: per
questo motivo m viene anche chiamato pendenza della retta.
Se m > 0
La retta y = mx + q forma con l’asse x un angolo
acuto
m>0
percorrendo la retta da
sinistra verso destra si
sale
angolo
acuto
Se m < 0
La retta y = mx + q forma con l’asse x un angolo
ottuso
m<0
percorrendo la retta da
sinistra verso destra si
scende
angolo
ottuso
Se m > 0
al crescere di m le rette y = mx + q formano con
l’asse x angoli acuti di ampiezza via via maggiore;
in altre parole: al crescere di m si ottengono rette
sempre più “ripide”
Se m < 0
al crescere di m le rette y = mx + q formano con
l’asse x angoli ottusi di ampiezza via via maggiore;
in altre parole: al crescere di m si ottengono rette
sempre meno “ripide”
m=2
m = -2
m=1
m = -1
m = 1/2
m = -1/2
L’equazione generale della retta nel piano cartesiano
L’equazione y = mx + q non permette di rappresentare tutte le rette del piano cartesiano, in quanto non
comprende le rette parallele all’asse y.
L’equazione che permette di rappresentare tutte le rette del piano è la seguente:
ax + by + c = 0
dove a, b e c sono numeri reali con a e b non entrambi nulli.
Se l’equazione di una retta è assegnata nella forma ax + by + c = 0 si dice che l’equazione è data in forma
implicita; se invece l’equazione di una retta è assegnata nella forma y = mx + q si dice che l’equazione è
data in forma esplicita.
Per passare dalla forma implicita alla forma esplicita basta risolvere l’equazione implicita rispetto a y.
Esempio: L’equazione 2x + 3y + 2 = 0 è l’equazione di una retta, data i forma implicita. Risolviamo questa
equazione rispetto a y:
2
2
2 x 3 y 2 0 3 y 2 x 2 y x
3
3
Abbiamo così ottenuto l’equazione della retta in forma esplicita.
Rette parallele
Due rette non parallele all’asse y, di equazioni y = mx + q e y = m’x + q’, sono parallele se e solo se hanno
lo stesso coefficiente angolare.
La condizione di parallelismo è quindi: m = m’
Rette perpendicolari
Due rette non parallele agli assi, di equazioni y = mx + q e y = m’x + q’, sono perpendicolari se e solo se i
loro coefficienti angolari hanno prodotto – 1.
La condizione di perpendicolarità è quindi:
1
m m 1
oppure m
m
Come determinare l’equazione di una retta
Sappiamo dalla geometria euclidea che una retta resta univocamente individuata quando se ne conoscono un
punto e la direzione, oppure due punti. Trasferendoci nell’ambito della geometria analitica, scaturiscono i
seguenti problemi:
a. determinare l’equazione di una retta passante per un punto P(x0,y0) e di coefficiente angolare m assegnato
(il coefficiente angolare individua la direzione della retta);
b. determinare l’equazione di una retta passante per due punti assegnati.
RETTA PASSANTE PER UN PUNTO E DI ASSEGNATO COEFFICIENTE ANGOLARE
L’equazione della retta passante per P( x0 , y0 ) e di coefficiente angolare m è: y y
0
mxx
0
Esempio: L’equazione della retta passante per P(– 2; 1) e di coefficiente angolare m = 2 è:
y 1 2x (2) y 2x 5
RETTA PASSANTE PER UN PUNTO E PARALLELA A UNA RETTA DATA
Esempio: Determiniamo l’equazione della retta passante per P( – 1; 3 ) e parallela alla retta r, di equazione
x 2y 1 0 .
1
1
1
x , quindi il suo coefficiente angolare è m
2
2
2
In base alla formula su scritta, l’equazione della retta passante per P( – 1; 3 ) e parallela alla retta r sarà:
1
1
7
y 3 x 1 da cui y x
2
2
2
L’equazione della retta r in forma esplicita è: y
RETTA PASSANTE PER UN PUNTO E PERPENDICOLARE A UNA RETTA DATA
Esempio: Determiniamo l’equazione della retta passante per P( 3; 0 ) e perpendicolare alla retta r, di
equazione y 2 x .
Il coefficiente angolare della retta r è 2; pertanto una retta perpendicolare a r deve avere coefficiente
1
1
1
angolare m' . La retta cercata è allora quella passante per P(3;0) e di coefficiente angolare
m
2
2
In base alla formula su scritta: y 0
1
x 3
2
da cui
y
1
3
x
2
2
RETTA PASSANTE PER DUE PUNTI
Vediamo come si determina l’equazione di una retta passante per due punti A(xA, yA) e B(xB, yB) assegnati.
Si dimostra che il coefficiente angolare m della retta passante per A(xA, yA) e B(xB, yB), con xA xB, è
y yA
y yA
, e pertanto la formula è y y A B
x x A
m B
xB x A
xB x A
Esempio: Determina l’equazione della retta passante per A(– 2, 4) e B(1, – 1).
y yA
1 4
5
m AB B
x B x A 1 2
3
y4
5
x (2)
3
ossia
y
5
2
x
3
3












