Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
1
1. Si risolvano tutti i circuiti mostrati negli esempi del Paragrafo
6 utilizzando la regola Shunt-Short, Serie-Sever .
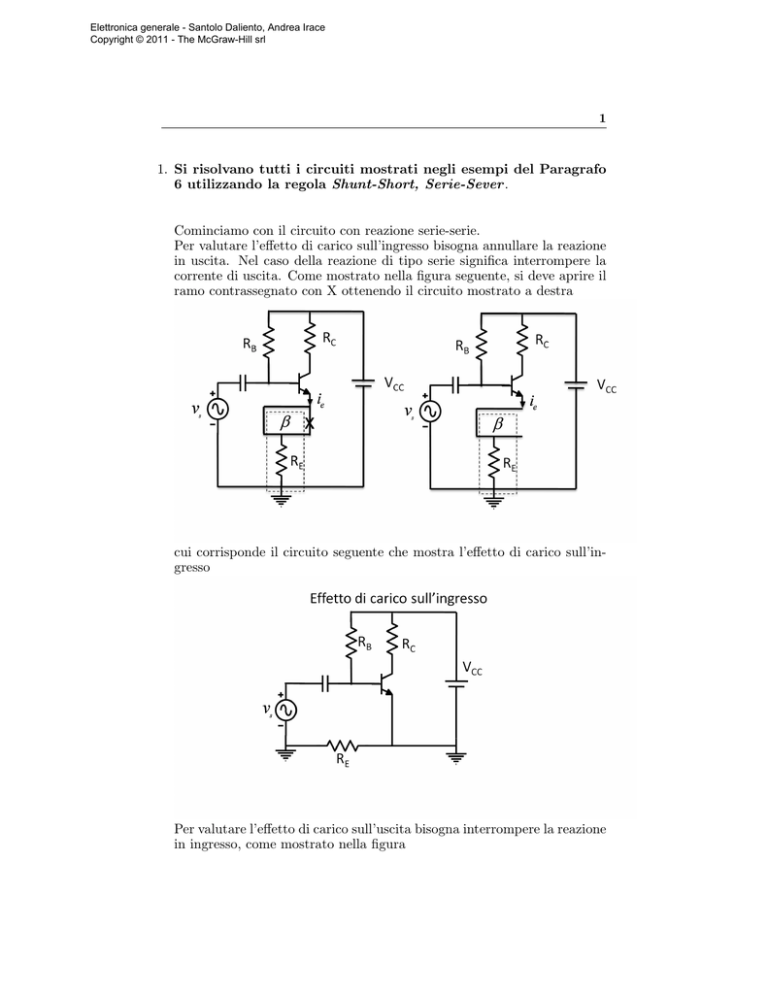
Cominciamo con il circuito con reazione serie-serie.
Per valutare l’effetto di carico sull’ingresso bisogna annullare la reazione
in uscita. Nel caso della reazione di tipo serie significa interrompere la
corrente di uscita. Come mostrato nella figura seguente, si deve aprire il
ramo contrassegnato con X ottenendo il circuito mostrato a destra
cui corrisponde il circuito seguente che mostra l’effetto di carico sull’ingresso
Per valutare l’effetto di carico sull’uscita bisogna interrompere la reazione
in ingresso, come mostrato nella figura
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
2
Capitolo 0
cui corrisponde l’effetto di carico sull’uscita
Pertanto, l’amplificatore base che comprende gli effetti di carico assume
la forma mostrata di seguito
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
3
A questo punto la soluzione dell’esercizio procede come mostrato negli
esempi.
Passiamo ora al circuito con reazione parallelo-parallelo.
Per annullare la reazione bisogna cortocircuitare i terminali della rete
di reazione con la massa. Per valutare l’effetto di carico sull’ingresso
cortocircuitiamo il terminale della rete di reazione posto sull’uscita, cosı̀
come mostrato in figura
ottenendo l’effetto di carico mostrato nella parte destra
Successivamente cortocircuitiamo il terminale posto sull’ingresso, ottenendo l’effetto di carico sull’uscita mostrato nella prossima figura
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
4
Capitolo 0
In definitiva l’amplificatore base che comprende gli effetti di carico della
rete di reazione appare come nella prossima figura
A questo si applicano le formule dei sistemi reazionati.
Infine, analizziamo il circuito con reazione serie-parallelo. Questa volta
bisogna aprire il terminale della rete di reazione posto sull’ingresso e
cortocircuitare quelllo posto sull’uscita.
Cortocircuitando il terminale sull’uscita, come mostrato nella figura seguente,
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
5
si ottiene l’effetto di carico sull’ingresso mostrato nella prossima figura
Aprendo il terminale posto sull’ingresso, come nella figura seguente
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
6
Capitolo 0
si ottiene l’effetto di carico sull’uscita mostrato nella prossima figura.
In conclusione, l’amplificatore base che comprende gli effetti di carico è
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
7
2. Con riferimento al circuito di Fig. 8.22 si determini l’espressione della resistenza di ingresso e la si confronti con quella
calcolata utilizzando il modello per piccolo segnale.
La teoria della reazione ci dice che nel caso di una connessione di tipo
serie in ingresso la resistenza di ingresso è pari alla resistenza di ingresso
dell’amplificatore base (che comprende gli effetti di carico) moltiplicata
per 1 + A∗ β, dove A∗ indica il guadagno dell’amplificatore base. Per
valutare la resistenza di ingresso dell’amplificatore base disegnamone il
circuito per piccolo segnale. Il circuito dell’amplificatore base lostesso
mostrato nell’esercizio precedente.
Dalla semplice ispezione visiva si comprende che la resistenza di ingresso
di questo circuito vale rπ +RE , quindi la resistenza di ingresso complessiva
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
8
Capitolo 0
vale (rπ + RE )(1 + A∗ β).
A questo punto bisogna ricordare che
A∗ = −
gm
1 + RrπE
e
β = RE
quindi
∗
A β=
gm RE
1 + RrπE
!
=
gm rπ RE
rπ + RE
=
βf RE
rπ + RE
dove con βf si è indicato il guadagno di corrente del BJT.
La resistenza di ingresso del circuito con reazione vale quindi
Rif = (rπ + RE )
βf RE
+1
rπ + RE
che si può scrivere
Rif = (βf RE + rπ + RE ) = rπ + RE (βf + 1)
quest’ultima relazione è del tutto identica a quella che si può ricavare
analizzando il modello per piccolo segnale completo del circuito di partenza oppure, più semplicemente, applicando il teorema della riflessione della
resistenza, il quale dice che la resistenza che si vede guardando nella base
è pari a rπ più la resistenza presente sul circuito di emettitore moltiplicata
per βf + 1
3. Con riferimento al circuito di Fig. 8.26 si determini l’espressione della resistenza di ingresso e la si confronti con quella
calcolata utilizzando il modello per piccolo segnale.
Procediamo come nel caso precedente ed analizziamo il modello per piccolo segnale corrispondente all’amplificatore base del circuito di Fig. 8.26.
Anche questo circuito è stato già disegnato per lo svolgimento del primo
esercizio, il suo equivalente per piccolo segnale è il seguente
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
9
Trattandosi di una reazione di tipo parallelo in ingresso questa volta la
resistenza di ingresso del circuito reazionato è data da quella dell’amplificatore base divisa per 1 + A∗ β.
Dal circuito si vede subito che la resistenza di ingresso dell’amplificatore
base vale RB //rπ .
D’altra parte ricordiamo che, per il circuito di Fig. 8.26 si è trovato che
β=
1
RB
e
A∗ = gm (RC //RB ) rπ //RB
quindi
A∗ β =
gm (RC //RB ) rπ //RB
RB
e
Rif =
1+
rπ //RB
gm (RC //RB )rπ //RB
RB
= RB
rπ //RB
RB + gm (RC //RB ) rπ //RB
esplicitando il parallelo tra rπ ed RB si ottiene facilmente
Rif =
rπ RB
RB + rπ + gm rπ (RC //RB )
Procediamo ora analizzando il circuito per piccolo segnale dell’ammplificatore completo, mostrato nella figura seguente
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
10
Capitolo 0
valutiamo la resistenza di ingresso Ri vista a valle di rπ , la resistenza di
ingresso complessiva sarà data dal parallelo tra Ri ed rπ . Per valutare
Ri riferiamoci al circuito seguente
dove il generatore di segnale vale vπ perchè quello è il valore della tensione
sulla base.
Dal circuito si ricava che
vπ = RB iB + Rc iC
e
iC = iB − gm vπ
da cui
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
11
vπ = RB iB + RC iB − gm vπ RC
risolvendo rispetto a vπ si trova
vπ (1 + gm RC ) = iB (RB + RC )
La resistenza Ri è data dal rapporto tra vπ e iB
Ri =
RB + RC
(1 + gm RC )
mentre la resistenza di ingresso complessiva, che chiamiamo Rif è data
da Ri in parallelo con rπ
Rif =
RB +RC
rπ (1+g
m RC )
rπ +
RB +RC
(1+gm RC )
=
rπ (RB + RC )
RB + RC + rπ + gm RC rπ
Dividendo numeratore e denominatore per RB + RC e moltiplicando
numeratore e denominatore per RB si ottiene
Rif =
RB +
rπ
R
1+ RC
rπ RB
+ gm rπ (RC //RB )
B
la quale è identica a quella trovata in precedenza quando RB >> RC
(tasso di reazione elevato) ed è, in tutti i casi, numericamente molto simile, perchè il termine con gm vπ (cioè il β del transistore) domina rispetto
agli altri.
4. Con riferimento al circuito di Fig. 8.30 si determini l’espressione della resistenza di uscita e la si confronti con quella calcolata utilizzando il modello per piccolo segnale.
Dal disegno dell’amplificatore base, riportato nella soluzione del primo
esercizio, si vede che il secondo stadio è un semplice amplificatore a doppio
carico, quindi la sua resistenza di uscita vale, come nell’amplificatore
a collettore comune, semplicemente re . Questo valore, già piccolo, va
ulteriormente diviso per 1 + A∗ β.
In questo caso
RC
A∗ =
RE1 //R
e
RE1
β=
RE1 + R
quindi
A∗ β =
RC RE1
RE1 R
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
12
Capitolo 0
e, in definitiva
Rof =
1+
re
RC RE1
RE1 R
L’analisi esatta risulta molto complessa, risulta più conveniente confrontarsi con una simulazione SPICE. Lasciamo al lettore questa verifica.
5. Con riferimento alla Fig. 8.33 si dimensioni il circuito in modo
che il guadagno di corrente sia pari a 20. Nelle condizioni cosı̀
determinate si valuti anche il guadagno di tensione.
Il guadagno di corrente del circuito complessivo è dato dal guadagno di
corrente dell’amplificatore base diviso per 1 + A∗ β. L’amplificatore base
assume la forma mostrata nella figura (Cfr. con gli esempi riportati nel
libro)
si tratta della cascata di un emettitore comune ed un doppio carico,
entrambi presentano guadagno di corrente pari a βf (a meno del partitore
di ingresso e del partitore sul secondo stadio). In prima approssimazione,
quindi, A∗ = βf 1 βf 2 dove con i pedici 1 e 2 sono indicati i guadagni di
corrente del primo e del secondo transistore.
Poichè
β=
R
R + RE1
Il guadagno di corrente complessivo sarà dato da
Aif =
βf 1 βf 2
R
1 + βf 1 βf 2 R+R
E1
Elettronica generale - Santolo Daliento, Andrea Irace
Copyright © 2011 - The McGraw-Hill srl
13
Se si suppone che il numeratore valga 104 (100 · 100) il valore del denominatore, per avere guadagno pari a 20, deve essere pari a 500. Imponendo
A∗ β = 500 si ottiene R ' 0.9RE1 .
Per calcolare il guadagno di tensione non si può procedere utilizzando
le formule della reazione negativa ed è più opportuno procedere con una
simulazione SPICE.












