ex cap 8

CORSO DI ECONOMIA POLITICA – DOCENTE LUIGI BOSCO – (25-49)
Esercizi: Domanda Offerta Sovrappiù, Elasticità
1 Nel mercato di un bene la funzione di domanda aggregata è
𝐷 = 300 − 3𝑝
e la funzione di offerta aggregata
0 𝑠𝑒 𝑝 < 36
{
𝑆 = 𝑝 − 36 𝑠𝑒 𝑝 ≥ 36
1a)
1b)
1c)
disegnare la retta di domanda e quella d’offerta
Calcolare il prezzo e la quantità scambiata di equilibrio
Calcolare il sovrappiù dei consumatori, dei produttori e quello aggregato.
2
Se la funzione di domanda aggregata è data dalla funzione Q = 100 - 2 P , come varia il surplus dei consumatori
(SC) se il prezzo aumenta da 20 a 30?
3
La funzione di domanda aggregata delle nocciole è Q d = a – b p. La funzione di offerta delle nocciole è
𝒑
𝑸𝒔 = 𝟎 𝒔𝒆 𝒑 < 𝟏
𝒄
{ 𝒔
𝒑
𝑸 = −𝒑𝟏 + 𝒄𝒑 𝒔𝒆 𝒑 ≥ 𝟏
𝒄
Se
3a)
a
b
c
p1
130
2
2
10
calcolate il prezzo e la quantità prodotta in equilibrio dal mercato
4
Considerando i valori della domanda precedente calcolate l’elasticità della domanda al prezzo nel punto di
equilibrio.
5
Se la funzione di domanda aggregata del caffè è Q D = a – b p . La funzione d’offerta delle imprese produttrici
𝒅
𝒅
di caffè è QSC = c p – d [quando 𝒑 ≥ , mentre QSC=0 quando 𝒑 < ], calcolate il sovrappiù aggregato nel
𝒄
𝒄
punto di equilibrio di concorrenza perfetta.
a
b
c
d
130
2
1
20
6 La funzione di domanda di un dato bene è Q = 150 – 3 p.
6a) Calcolate l’elasticità puntuale del bene in questione quando il prezzo è 10.
6b) Calcolate per quale valore di p l’elasticità assume valore unitario.
7
7a)
La funzione di domanda aggregata delle melanzane è QM = a – b p. Al momento il prezzo delle melanzane è
p1.
Come varierebbe la spesa totale dei consumatori per le melanzane (STM)se il prezzo avesse un lieve
(infinitesimo) aumento ? Cosa succederebbe alla spesa totale per le melanzane in caso di lieve aumento del
prezzo se il prezzo iniziale fosse p1 ? E se il prezzo iniziale fosse p2?
a
b
p1
p2
100
4
10
15
Soluzioni: Domanda Offerta Sovrappiù Elasticità
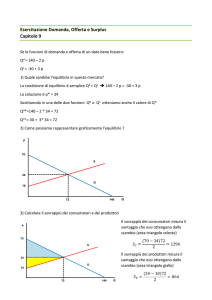
1 Nel mercato di un bene la funzione di domanda aggregata è
𝐷 = 300 − 3𝑝
e la funzione di offerta aggregata
0 𝑠𝑒 𝑝 < 36
{
𝑆 = 𝑝 − 36 𝑠𝑒 𝑝 ≥ 36
1) disegnare la funzione le due funzioni
2) Calcolare il prezzo e la quantità scambiata di equilibrio
3) Calcolare il sovrappiù dei consumatori, dei produttori e quello aggregato.
1a)
p
𝑁𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑑 ′ 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑡𝑡𝑎 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙𝑒
𝑄 = 0 𝑞𝑢𝑖𝑛𝑑𝑖
0 = 300 − 3𝑝
300
𝑝=
= 100
3
S
100
𝑁𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑑 ′ 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑡𝑡𝑎 𝑜𝑟𝑖𝑧𝑧𝑜𝑛𝑡𝑎𝑙𝑒
𝑃 = 0 𝑞𝑢𝑖𝑛𝑑𝑖
𝑄 = 300 − 3(0) = 300
36
1b)
{
𝑄 = 0 𝑞𝑢𝑖𝑛𝑑𝑖
p = 36
D
300
Per trovare l’equilibrio occorre imporre la condizione D = S ovvero
Q
𝐷 = 𝑆 = 0 𝑠𝑒 𝑝 < 36
300 − 3𝑝 = 𝑝 − 36 𝑠𝑒 𝑝 ≥ 36
336 = 4𝑝 → 𝑝 =
Considerando il caso nel quale p ≥ 36
336
4
= 84
sostituendo per p nella funzione di domanda o in quella di offerta otteniamo
𝐷 = 300 − 3 ∗ 84 = 300 − 252 = 48
p
𝑆 = 84 − 36 = 48
S
1c)
Sovrappiù consumatori 𝑆𝐶 =
Sovrappiù imprese 𝑆𝑃 =
(100−84)48
2
(84−36)48
Sovrappiù aggregato = 1536
2
=384
100
84
= 1152
36
D
48
300
Q
2
3
La formula dell’elasticità è η =
4
dQ
dp
dQ p
dp Q
= −2 (il coefficiente angolare della funzione di domanda lineare), p = 35 e Q=60; quindi
η = −𝟐
5
35
𝟕
=−
60
𝟔
In questo caso
QS = Qd  -20 + p = 130 + 2p
3p = 150  p=50
Q=130-2(50) = 30.
𝑆𝐶 =
(65 − 50)30
= 225
2
𝑆𝑃 =
(50 − 20)30
= 450
2
SA = 675
6
La formula dell’elasticità è η =
6a)
dQ
dp
dQ p
dp Q
= −3.e p = 10
Dobbiamo conoscere il valore di Q sostituendo p=10 nella FdD
Q = 150 – 3(10)= 120
quindi
η = −𝟑
6b)
10
𝟏
=−
120
𝟒
Per rispondere alla domanda possiamo
o ricordare che l’elasticità assume valore unitario nel punto mediano della FdD, quindi quando Q=75 (75=150/2)
e p = 25,
infatti
η = −𝟑
25
75
= −𝟏
o procedere algebricamente
P
Q
1
3
1
3
η = −1 = −3  𝑝 = 𝑄 sostituendo nella FdD otteniamo 𝑄 = 150 − 3 𝑄 2Q=150  Q = 75, p =25
7
Per sapere cosa accade alla spesa totale quando varia il prezzo dobbiamo derivare la spesa totale rispetto al
prezzo ottenendo:
dST
dQ(P)
 dQ(P) P 
 Q(P)  P
 Q(P) 1 
 Q(P)1    Q(P)1   
dP
dP
dP Q 

dST
 0 se 1     0  se   1
dP
dST
 0 se 1     0  se   1
dP
E’ evidente che quel che succede alla spesa totale quando aumenta il prezzo dipende dal valore dell’elasticità.
 Se la domanda è rigida (η<1 in valore assoluto) la spesa totale aumenta quando aumenta il prezzo perché la
variazione del prezzo domina la variazione della quantità.
 Se la domanda è elastica (η>1 in valore assoluto) la spesa totale diminuisce quando aumenta il prezzo perché
la variazione della quantità domina la variazione del prezzo.
Quindi è sufficiente calcolare il valore delle elasticità della domanda nei due punti indicati per rispondere alla
domanda
(p  10)  4
10
2

60
3
(p  15)  4
15
3

40
2
La spesa totale aumenta
La spesa totale diminuisce