SEZIONE O «ONDE
Muscolo
ciliare
Cornea
Retina
Nervo
ottico
Umore
acqueo
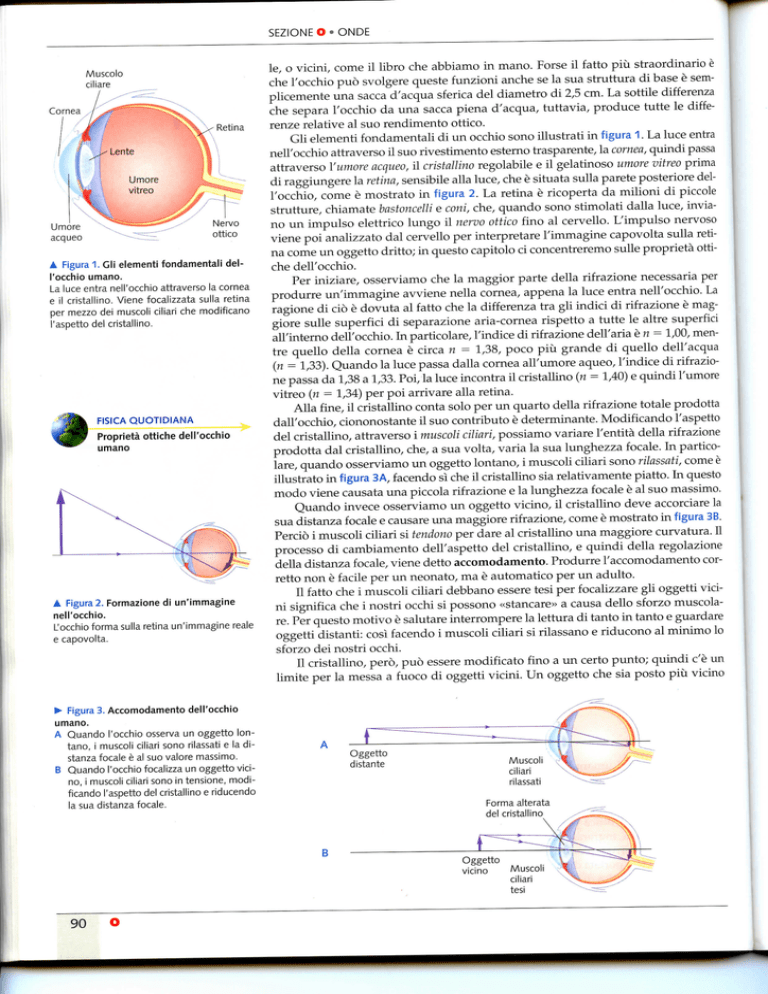
A Figura 1. Gli elementi fondamentali dell'occhio umano.
La luce entra nell'occhio attraverso la cornea
e il cristallino. Viene fecalizzata sulla retina
per mezzo dei muscoli ciliari che modificano
l'aspetto del cristallino.
FISICA QUOTIDIANA
Proprietà ottiche dell'occhio
umano
A Figura 2. Formazione di un'immagine
nell'occhio.
L'occhio forma sulla retina un'immagine reale
e capovolta.
^ Figura 3. Accomodamento dell'occhio
umano.
A Quando l'occhio osserva un oggetto lontano, i muscoli ciliari sono rilassati e la distanza focale è al suo valore massimo.
B Quando l'occhio fecalizza un oggetto vicino, i muscoli ciliari sono in tensione, modificando l'aspetto del cristallino e riducendo
la sua distanza focale.
le, o vicini, come il libro che abbiamo in mano. Forse il fatto più straordinario è
che l'occhio può svolgere queste funzioni anche se la sua struttura di base è semplicemente una sacca d'acqua sferica del diametro di 2,5 cm. La sottile differenza
che separa l'occhio da una sacca piena d'acqua, tuttavia, produce tutte le differenze relative al suo rendimento ottico.
Gli elementi fondamentali di un occhio sono illustrati in figura 1. La luce entra
nell'occhio attraverso il suo rivestimento esterno trasparente, la cornea, quindi passa
attraverso l'umore acqueo, il cristallino regolabile e il gelatinoso umore vitreo prima
di raggiungere la retina, sensibile alla luce, che è situata sulla parete posteriore dell'occhio, come è mostrato in figura 2. La retina è ricoperta da milioni di piccole
strutture, chiamate bastoncelli e coni, che, quando sono stimolati dalla luce, inviano un impulso elettrico lungo il nervo ottico fino al cervello. L'impulso nervoso
viene poi analizzato dal cervello per interpretare l'immagine capovolta sulla retina come un oggetto dritto; in questo capitolo ci concentreremo sulle proprietà ottiche dell'occhio.
Per iniziare, osserviamo che la maggior parte della rifrazione necessaria per
produrre un'immagine avviene nella cornea, appena la luce entra nell'occhio. La
ragione di ciò è dovuta al fatto che la differenza tra gli indici di rifrazione è maggiore sulle superfici di separazione aria-cornea rispetto a tutte le altre superfici
all'interno dell'occhio. In particolare, l'indice di rifrazione dell'aria è n = 1,00, mentre quello della cornea è circa n = 1,38, poco più grande di quello dell'acqua
(n = 1,33). Quando la luce passa dalla cornea all'umore aqueo, l'indice di rifrazione passa da 1,38 a 1,33. Poi, la luce incontra il cristallino (n = 1,40) e quindi l'umore
vitreo (n = 1,34) per poi arrivare alla retina.
Alla fine, il cristallino conta solo per un quarto della rifrazione totale prodotta
dall'occhio, ciononostante il suo contributo è determinante. Modificando l'aspetto
del cristallino, attraverso i muscoli ciliari, possiamo variare l'entità della rifrazione
prodotta dal cristallino, che, a sua volta, varia la sua lunghezza focale. In particolare, quando osserviamo un oggetto lontano, i muscoli ciliari sono rilassati, come è
illustrato in figura 3A, facendo sì che il cristallino sia relativamente piatto. In questo
modo viene causata una piccola rifrazione e la lunghezza focale è al suo massimo.
Quando invece osserviamo un oggetto vicino, il cristallino deve accorciare la
sua distanza focale e causare una maggiore rifrazione, come è mostrato in figura 3B.
Perciò i muscoli ciliari si tendono per dare al cristallino una maggiore curvatura. Il
processo di cambiamento dell'aspetto del cristallino, e quindi della regolazione
della distanza focale, viene detto accomodamento. Produrre l'accomodamento corretto non è facile per un neonato, ma è automatico per un adulto.
Il fatto che i muscoli ciliari debbano essere tesi per fecalizzare gli oggetti vicini significa che i nostri occhi si possono «stancare» a causa dello sforzo muscolare. Per questo motivo è salutare interrompere la lettura di tanto in tanto e guardare
oggetti distanti: così facendo i muscoli ciliari si rilassano e riducono al minimo lo
sforzo dei nostri occhi.
Il cristallino, però, può essere modificato fino a un certo punto; quindi c'è un
limite per la messa a fuoco di oggetti vicini. Un oggetto che sia posto più vicino
Oggetto
distante
Forma alterata
del cristallino
Oggetto
vicino
90
Muscoli
ciliari
tesi
3 - STRUMENTI OTTICI
< L'iride pigmentata dell'occhio umano risponde automaticamente ai cambiamenti di
intensità dell'illuminazione, dilatando la pupilla con la luce debole e contraendola con la
luce intensa.
^
all'occhio del suo punto prossimo, N, appare sfocato, indipendentemente da quanto ci sforziamo di metterlo a fuoco. Per un giovane, la distanza del punto prossimo è normalmente di circa 25 cm, ma essa aumenta con il passare degli anni. Una
persona di 40 anni può avere il suo punto prossimo a 40 cm, in tarda età può trovarlo anche oltre i 500 cm. Perciò invecchiando, di solito, è necessario allontanare
il foglio per poterlo leggere e inforcare gli occhiali.
Invece il punto remoto è la più grande distanza alla quale può trovarsi un
oggetto dall'occhio ed essere ancora a fuoco. Poiché possiamo mettere a fuoco la
Luna e le stelle, è evidente che normalmente il punto remoto è all'infinito.
Infine, la quantità dì luce che raggiunge la retina è controllata da un diaframma colorato chiamato iride. Allargandosi e restringendosi, l'iride regola le dimensioni della pupilla, l'apertura attraverso la quale la luce entra nell'occhio. Con la
luce intensa la pupilla si chiude fino a un diametro di 1 mm. Nelle notti più buie,
la pupilla adattata all'oscurità può aprirsi fino a un diametro di circa 7 mm.
1.ESEMP O SVOLTO
Escursione al punto prossimo
La distanza del punto prossimo di un dato occhio è N = 25 cm. Trattando l'occhio come se fosse una singola
lente a distanza di 2,5 cm dalla retina, trova la distanza focale della lente, quando viene messo a fuoco un
oggetto:
a. nel punto prossimo;
b. all'infinito.
• Descrizione
Nella figura sono illustrati l'occhio e l'equivalente semplificazione della lente sottile. Osserviamo che l'asse orizzontale è spezzato al fine di poter mettere l'oggetto e l'occhio nello stesso disegno.
• Strategia
Troviamo la distanza focale utilizzando l'equazione delle lenti sottili, l/d0 + \l&\ I//. La distanza dell'immagine è d-, = 2,5 cm
sia nel caso a. sia nel caso b.. Nel caso a. la distanza dell'oggetto è d0 = 25 cm; nel caso b. è da = =°.
• Soluzione
a.
1. Sostituiamo d0 = 25 cm e di = 2,5 cm nell'equazione
delle lenti sottili e ricaviamo/
i
=
_L + _L = 25 cm
|
:
2,5 cm
= Q 44 cm"1
= 2,3 cm
£
0,44 cm"
O
91
3 « STRUMENTI OTTICI
Mostriamo ora come un sistema di due lenti (l'occhio e una lente esterna) può
correggere un difetto della vista.
Miopia
Se una persona con una vista normale rilassa i muscoli ciliari dell'occhio, riesce a
mettere a fuoco un oggetto all'infinito. In una persona miope, invece, l'occhio totalmente rilassato vede chiaramente solo a una certa distanza finita: il punto remoto;
cioè, una persona miope mette a fuoco solo gli oggetti vicini all'occhio, mentre
quelli oltre il punto remoto risultano confusi.
Il problema in questo caso è che l'occhio fa convergere la luce a una distanza
troppo breve; in altre parole, la distanza focale dell'occhio è inferiore al diametro
dell'occhio. Tale condizione è illustrata in figura 6, dove vediamo che un oggetto
all'infinito forma un'immagine davanti alla retina, a causa dell'allungamento dell'occhio. Non occorre che questo effetto sia grande; come abbiamo visto nel precedente paragrafo, un allungamento di solo un millimetro o due è sufficiente per
provocare un problema.
Per correggere questo difetto dobbiamo annullare l'eccesso di convergenza
prodotto dall'occhio, in modo che l'immagine cada di nuovo sulla retina. Per fare
ciò poniamo una lente divergente davanti all'occhio. In particolare, consideriamo un
oggetto all'infinito, che a una persona miope normalmente appare confuso. Se una
lente concava, con un'opportuna distanza focale, produce un'immagine di tale oggetto nel punto remoto di questa persona, come in figura 7, l'occhio rilassato potrà
mettere a fuoco l'oggetto. Esaminiamo questa situazione nel prossimo esempio
svolto.
Visione
confusa
-
PROBUEM SOLVINC
Correggere la miopia
Per correggere la miopia si deve utilizzare
una lente che produce un'immagine sul
punto remoto della persona quando l'oggetto si trova all'infinito. Osserva che il
punto remoto è più vicino alle lenti di un
paio di occhiali che non all'occhio, poiché
gli occhiali sono davanti agli occhi.
•^ Figura 6. Forma dell'occhio e miopia.
La forma allungata dell'occhio può essere la
causa della miopia. In questo caso, un oggetto all'infinito viene messo a fuoco davanti alla
retina.
-^ Figura 7. Correzione della miopia.
Una lente divergente davanti all'occhio può
correggere la miopia. La lente concava focalizza la luce 'proveniente da un oggetto che si
trova oltre il punto remoto in modo da produrre un'immagine nel punto remoto. L'occhio così può mettere a fuoco l'immagine dell'oggetto.
Immagine formata
da una lente concava
Visione estesa
Una persona miope ha il punto remoto a 323 cm dall'occhio.
;
Se le lenti di un paio di occhiali sono a 2,00 cm dagli occhi, che distanza focale devono avere per consentirle
di mettere a fuoco oggetti lontani?
4. ESEMPIO SVOLTO
Fisica
quotidiana
• Descrizione
Nella figura sono mostrati un oggetto all'infinito e l'immagine prodotta da una lente concava. L'immagine è nel punto remoto dell'occhio della persona.
Oggetto
Immagine dell'oggetto
prodotta da una lente concava
all'infinito
• Strategia
Possiamo trovare la distanza focale della lente utilizzando l'equazione delle lenti sottili l/d 0 + 1/d, = I//.
In questo caso d0 = =0, poiché l'oggetto è infinitamente lontano.
L'immagine è a 323 cm dall'occhio, cioè 323 cm — 2,00 cm = 321 cm
dalla lente. Perciò la distanza dell'immagine è di = 321 cm.
Con questi valori di d0 e d\o la distanza focale/.
95
SEZIONE O » ONDE
• Soluzione
1. Sostituiamo d0 = « e d; = 321 cm nell'equazione delle lenti sottili
JL 1 _ ì - L
2. Ricaviamo la distanza focale/
/ = -321 cm
d0
d(
/
*
_1
-321 cm
• Osservazioni
Con una lente con questa distanza focale la persona può mettere a fuoco gli oggetti distanti con gli occhi rilassati.
• Problema
Se questi occhiali vengono utilizzati per vedere un oggetto posto a 525 cm dall'occhio, calcola a quale distanza dall'occhio viene prodotta l'immagine dalla lente concava.
Problemi simili: 25, 27 e 28 a pag, O112 e Olii.
> Figura 8. Potere diottrico.
Una lente con una minore distanza focale,
come in B, ha maggiore potere diottrico di
una con una maggiore distanza focale, come
in A, nel senso che i raggi di luce entranti vengono deviati maggiormente.
B
La capacità di una lente di rifrangere la luce, potere diottrico, è legata alla sua
distanza focale. Minore è la distanza focale, maggiore è la rifrazione della luce da
parte della lente, come è mostrato in figura 8. Perciò il potere diottrico dipende
inversamente dalla distanza focale. Per definizione, quindi, diciamo che il potere
diottrico di una lente è I//, dove fé misurato in metri:
Potere diottrico o diottria
diottria = rrr1
potere diottrico = —
3.2
Normalmente le lenti sono caratterizzate dagli ottici, con le diottrie piuttosto che
con la distanza focale.
Come esempio sul significato di diottria, consideriamo che una lente con un
potere diottrico di 10 diottrie ha una distanza focale di I/(10 irT1) = 10 cm (lente
convergente), mentre una lente con un potere diottrico di —10 diottrie ha una
distanza focale di -10 cm (lente divergente).
Nell'esempio svolto 4 la lente necessaria per correggere la miopia ha un potere diottrico di l/(-3,21 m) = -0,312 diottrie.
5. ESEMPIO GUIDATO
Diottrie
Una persona ha il punto remoto a 5,50 m dai suoi occhi.
Se questa persona mette gli occhiali a 2,00 cm dagli occhi, calcola quale potere
diottrico, in diottrie, devono avere le lenti.
• Soluzione
A Per prescrivere le opportune lenti correttive è necessario misurare le proprietà rifrangenti dell'occhio del paziente. Questo strumento consente all'optometrista di vedere
come lenti con differenti caratteristiche ottiche modificano la vista del paziente.
1. Identifichiamo la distanza dell'oggetto
2. Identifichiamo la distanza dell'immagine
3. Utilizziamo l'equazione delle lenti sottili
per calcolare la distanza focale delle lenti
4. Trasformiamo/in metri e invertiamo il risultato
per trovare il potere diottrico
d0 = <*
d; = — 548 cm
/ = — 548 cm
potere diottrico = -0,182
• Osservazioni
II fatto che il punto remoto di questa persona sia più lontano (vicino all'infinito) del
punto remoto dell'esempio svolto 4 significa che le lenti non devono essere così «forti»
per correggere questo difetto. Di conseguenza, il numero di diottrie qui è minore di
quello dell'esempio svolto 4.
96
3 « STRUMENTI OTTICI
Al giorno d'oggi, in aggiunta agli occhiali e alle lenti a contatto, esistono numerose tecniche mediche per correggere la miopia. Alcune di queste procedure prevedono l'utilizzazione di un fascio di luce laser per ricostruire la forma della cornea.
Esamineremo queste tecniche quando studieremo in dettaglio i laser. Qui presentiamo due tecniche alternative che modificano la forma di una cornea con mezzi
meccanici.
Forse la più semplice di queste tecniche è l'impianto di un anello intmcorneale
o Intact nella cornea. Un Intact consiste di due piccole mezzelune trasparenti, dello
stesso materiale utilizzato per le lenti a contatto, che vengono infilate in solchi praticati nella cornea. Quando le mezzelune sono in posizione tendono a tirare la cornea verso l'esterno e ad appiattire la sua superficie. Questo appiattimento aumenta
la distanza focale e corregge la miopia da -1 a -3 diottrie. Se necessario, l'Intact
può essere rimosso e sostituito con altri che producono un maggiore o minore
appiattimento della cornea.
Un metodo più complesso coinvolge l'effettuazione di incisioni radiali per
mezzo di una lama di diamante ad alta precisione, che taglia a una determinata
profondità. Tale metodo viene chiamato cheratotomia radiale o RK (figura 9). Queste
incisioni permettono alle parti periferiche della cornea di gonfiarsi verso l'esterno,
il che, a sua volta, determina l'appiattimento della parte centrale. Come con l'Intact,
l'appiattimento della cornea corregge la miopia.
Ipermctropia
Una persona ipermetrope può vedere chiaramente oltre una determinata distanza, punto prossimo, ma non riesce a mettere a fuoco gli oggetti più vicini.
Fondamentalmente, la visione di un ipermetrope differisce da quella di una persona con una vista normale per il fatto di avere il punto prossimo più lontano. Di
conseguenza, un ipermetrope non riesce a leggere facilmente, poiché un libro
dovrebbe essere tenuto a grande distanza per risultare a fuoco.
L'ipermetropia può essere causata da un bulbo oculare più corto del normale,
come è illustrato in figura 10. In questo caso i raggi provenienti da un oggetto più
vicino del punto prossimo convergono in un punto dietro alla retina. Perciò la
distanza focale di un ipermetrope è troppo grande, cioè l'occhio di un ipermetrope non fa convergere la luce entrante abbastanza da fecalizzarla sulla retina.
Questo problema può essere corretto facendo «preconvergere» la luce, cioè utilizzando una lente convergente davanti agli occhi, per rinforzare la convergenza
insufficiente. Supponiamo che un oggetto sia più vicino del punto prossimo, come
in figura 11; se una lente convergente posta davanti agli occhi può produrre un'immagine oltre il punto prossimo, l'ipermetrope può vedere l'oggetto chiaramente.
Esamineremo un sistema di questo tipo nel prossimo esempio svolto.
r
_Visione i Visione
chiara ' confusa
Immagine formata
dalla lente convessa
Oggetto vicino "
al punto prossimo
FISICA QUOTIDIANA
Anello intracorneale
FISICA QUOTIDIANA
Cheratotomia radiale
Incisione
A Figura 9. Cheratotomia radiale.
Nella cheratotomia radiale viene fatta una
serie di incisioni radiali alla periferia della cornea. Ciò consente alla cornea di espandersi
verso l'esterno, appiattendo la regione centrale. La diminuzione della curvatura della
cornea fa aumentare la distanza focale dell'occhio, permettendogli di mettere a fuoco
gli oggetti lontani.
•< Figura 10. Forma dell'occhio e ipermetropia.
Un occhio più corto del normale può soffrire
di ipermetropia. Osserviamo che un oggetto
che si trova più vicino del punto prossimo
viene messo a fuoco dietro la retina.
•* Figura 11. Correzione dell'ipermetropia.
Una lente convessa davanti all'occhio può
correggere l'ipermetropia. La lente convessa
fecalizza la luce proveniente da un oggetto
più vicino del punto prossimo per produrre
un'immagine oltre il punto prossimo. L'occhio,
così, può mettere a fuoco l'immagine dell'oggetto.
97
SEZIONE O «ONDE
6. ESEMP O SVOLTO
Guardi lontano
Fisica
Un ipermetrope mette gli occhiali per poter leggere un libro tenuto a una distanza di 25,0 cm dai suoi occhi,
quotidiana anche se il suo punto prossimo è a una distanza di 57,0 cm.
J
Se gli occhiali sono a 2,00 cm dagli occhi, trova la distanza focale e il potere diottrico necessari affinchè le lenti formino un'immagine del libro nel punto prossimo di questa persona.
• Descrizione
Nella figura è illustrata la situazione fisica. Osserviamo che l'immagine del libro è nel punto prossimo.
Immagine del libro Libro posto
formata dalla
prima del punto
lente convessa
prossimo
• Strategia
Troviamo la distanza focale della lente utilizzando l'equazione
delle lenti sottili. La distanza dell'oggetto è da = 23,0 cm, tenendo
conto dei 2,00 cm fra gli occhiali e gli occhi. Analogamente, la
distanza desiderata per l'immagine èd[= —55,0 cm. Il segno meno è necessario per la distanza, perché l'immagine si trova dalla
stessa parte dell'oggetto rispetto alla lente.
/
Punto
prossimo
i
i
i
i
i 2 00
32,0 cm— K23,0 crrH— -=—i
i crn
• Soluzione
= 0,0253 cm"
1. Utilizziamo l'equazione delle lenti sottili
per trovare la distanza focale/
23,0 cm
i
/ = 0,0253 cm"
2. Il potere diottrico è I// con/misurato in metri
-55,0cm
= 39,5 cm
1
1
potere diottrico = — =
= 2,53 diottrie
/
0,395 m
• Osservazioni
Osserviamo che il libro si trova fra la lente e il fuoco. Di conseguenza l'immagine è dritta (vedi la figura 34B del capitolo O2), come
è opportuno per gli occhiali da lettura.
• Problema
Un'altra persona ha il proprio punto prossimo a una distanza maggiore di 57,0 cm.
In questo caso, il potere diottrico delle lenti necessarie è maggiore o minore di 2,53 diottrie? Verifica la tua risposta, calcolando
il potere diottrico per un punto prossimo a una distanza di 67,0 cm.
Problemi simili: 24 e 29 a pag. O112 e O113.
VERIFICA DEI CONCETTI
-C
PROBLEM SOLVING
Correzione dell'ipermetropia
Per correggere l'ipermetropia, dobbiamo
utilizzare lenti che producono un'immagine
alla distanza del punto prossimo della persona quando l'oggetto è più vicino del punto prossimo. Osserviamo che la distanza tra
l'oggetto e le lenti degli occhiali è minore
della distanza tra l'oggetto e gli occhi.
Marco e Giovanni sono in campeggio e decidono di accendere un fuoco con un paio di
occhiali, utilizzando la luce del Sole. Sapendo che Marco è miope e Giovanni è ipermetrope,
indica quale paio di occhiali devono utilizzare:
E quelli di Marco
O quelli di Giovanni
• Discussione
Per fecalizzare i raggi paralleli della luce del Sole in un punto sono necessarie delle lenti convergenti. Come abbiamo visto, la miopia viene corretta con una lente divergente; l'ipermetropia, invece, viene corretta con una lente convergente. Gli occhiali di Giovanni sono
convergenti e quindi sono quelli da utilizzare per accendere il fuoco.
Risposta
Gli occhiali di Giovanni sono la scelta migliore.
98












