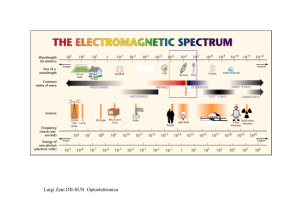
Mezzi anisotropi
I mezzi otticamente anisotropi (tipicamente cristalli non cubici) sono
mezzi in cui le proprietà ottiche dipendono dalla direzione. In
particolare, la costante dielettrica ε, che dipende dallo spostamento
degli elettroni rispetto ai nuclei, assume valori diversi a seconda
della direzione cristallina; cioè gli elettroni sono più o meno legati ai
nuclei a seconda della direzione in cui sono forzati a muoversi.
L’indice di rifrazione di un cristallo anisotropo dipende, quindi, dalla
direzione del campo elettrico dell’onda che lo attraversa.
Per i cristalli otticamente anisotropi la permeabilità magnetica è quella
del vuoto mentre la costante dielettrica è descrivibile con una matrice
3X3 detta tensore dielettrico.
I vettori E e D non sono paralleli
Luigi Zeni DII-SUN Optoelettronica
ε11 ε12
ε = ε 21 ε 22
ε
31 ε 32
ε13
ε 23
ε 33
Mezzi anisotropi
In un opportuno sistema di riferimento (assi coincidenti con gli assi
principali del cristallo) il tensore dielettrico si scrive:
εx
ε= 0
0
0
εy
0
0
0
ε z
Dalle equazioni di Maxwell nel dominio della frequenza in assenza di
cariche e correnti libere:r r
r
r
1 r r
k × E = ωB
H=
k×E
µω
r r
r
r
1r r
k × H = − ωD
D =− k×H
ω
r r
r r
r r
k⋅D = 0
k ⋅ B = µk × H = 0
H e D sono ortogonali a k mentre E in generale non è ortogonale a k
Luigi Zeni DII-SUN Optoelettronica
Cristalli biassici e uniassici
Il tensore dielettrico può avere tutti gli elementi diversi o solo due
diversi tra loro.
Nel primo caso si parla di cristalli biassici, nel secondo di cristalli
uniassici.
εx
n1 =
ε0
n2 =
εy
ε0
εz
n3 =
ε0
Gli indici di rifrazione corrispondenti ai tre elementi del tensore
dielettrico sono detti indici di rifrazione principali e corrispondono
allo stato di polarizzazione dell’onda lungo i tre assi principali del
cristallo rappresentato mediante l’ellissoide di Fresnel o degli indici
Luigi Zeni DII-SUN Optoelettronica
Birifrangenza
Si dimostra che in un cristallo uniassico sono ammessi solo due stati
di polarizzazione per il vettore D.
Un’onda non polarizzata che entra in un cristallo uniassico ad
opportuno angolo si divide in due onde che si propagano a velocità
diversa delle quali una segue la legge di Snell e viene detta onda
ordinaria mentre l’altra non segue la legge di Snell e viene detta
onda straordinaria. Si parla di doppia rifrazione o birifrangenza.
Mezzo isotropo
Luigi Zeni DII-SUN Optoelettronica
Mezzo anisotropo
Cristalli uniassici
Nei cristalli uniassici si pone n1=n2=no (indice ordinario) e
n3=ne (indice straordinario).
ne > no
cristallo uniassico positivo
ne < no
cristallo uniassico negativo
L’indice ordinario non dipende dalla direzione di propagazione
L’indice straordinario dipende dalla direzione di propagazione
Luigi Zeni DII-SUN Optoelettronica
Cristalli uniassici
L’indice straordinario si può determinare graficamente mediante
l’ellissoide di Fresnel che in questo caso è un ellissoide di
rivoluzione intorno all’asse z detto asse ottico del cristallo
no e ne rappresentano le ampiezze dei semiassi dell’ellissoide
Luigi Zeni DII-SUN Optoelettronica
Cristalli uniassici
Un’onda che si propaga lungo l’asse ottico vede il cristallo come
isotropo con indice di rifrazione no.
Un’onda che si propaga ortogonalmente all’asse ottico vede un
indice ordinario pari a no e un indice straordinario pari ne
In generale si ha:
Luigi Zeni DII-SUN Optoelettronica
cos 2 θ sin 2 θ
=
+ 2
2
2
n e (θ)
no
ne
1
Cristalli uniassici
La direzione del vettore di Poynting per l’onda straordinaria è
diversa dalla direzione del vettore ke quindi il fronte di fase
viaggia in direzione diversa dal flusso di energia (walk-off del
vettore di Poynting).
La direzione del “raggio” è sempre quella del vettore di Poynting.
Luigi Zeni DII-SUN Optoelettronica
Indici di cristalli notevoli per λ = 589nm
Isotropi
Diamante
Fluorite (CaF2)
no
2.4170
1.4340
ne
2.4170
1.4340
Ghiaccio
Quarzo
Rutile (TiO2)
no
1.3090
1.5442
2.6160
ne
1.3105
1.5533
2.9030
no
1.6580
2.2900
ne
1.4860
2.2000
n1
1.5601
n2
n3
1.5936 1.5977
Uniassici positivi
Uniassici negativi
Biassici
Calcite (CaCO3)
Niobato di Litio
(LiNBO3)
Mica
Luigi Zeni DII-SUN Optoelettronica
Birifrangenza della calcite
Un’onda incidente lungo una direzione diversa dall’asse ottico viene
divisa in due onde con polarizzazione ortogonale.
Luigi Zeni DII-SUN Optoelettronica
Dicroismo
Alcuni materiali anisotropi manifestano un fenomeno secondo il quale
il coefficiente di assorbimento dipende dalla direzione di propagazione
dallo stato di polarizzazione dell’onda.
Tale fenomeno è noto come DICROISMO
Un’onda di polarizzazione arbitraria che attraversa un mezzo dicroico,
di opportuna lunghezza, emerge con una polarizzazione ben definita.
Ad esempio la tormalina (borosilicato di alluminio) esibisce dicroismo
Luigi Zeni DII-SUN Optoelettronica
Applicazioni dei materiali birifrangenti
Alcuni importanti dispositivi passivi, molto usati in optoelettronica,
vengono realizzati mediante materiali birifrangenti:
•Polarizzatori
•Lamine di ritardo
•Compensatori di ritardo
•Prismi divisori di polarizzazione
Luigi Zeni DII-SUN Optoelettronica
Polarizzatori
Possono essere realizzati ad esempio con:
a) due prismi di calcite tagliati ad angolo opportuno (68°) ed incollati
con uno speciale materiale in modo tale che all’interfaccia con il
collante l’onda ordinaria subisce riflessione totale mentre quella
straordinaria viene trasmessa.
b) materiali dicroici
Legge di Malus:
I(θ) = I(0 ) cos 2 θ
Luigi Zeni DII-SUN Optoelettronica
Altri tipi di polarizzatori
Polarizzatore di
Glan-Foucault
Polarizzatore a
fili metallici
Luigi Zeni DII-SUN Optoelettronica
Lamine di ritardo
Se una lamina di materiale uniassico (es. positivo) viene realizzata con
l’asse ottico parallelo alla faccia di ingresso, due onde linearmente
polarizzate con il campo elettrico rispettivamente parallelo e ortogonale
all’asse ottico, risultano all’uscita ritardate in fase l’una rispetto all’altra.
Se l’asse ottico è invece ortogonale alla faccia di ingresso le due onde
non subiscono ritardo di fase.
Luigi Zeni DII-SUN Optoelettronica
Lamine di ritardo
Se un’onda è polarizzata linearmente con un angolo α rispetto all’asse
ottico, parallelo alla faccia di ingresso della lamina, le due componenti
viaggiano con velocità diversa (asse lento e asse veloce) ed emergono
con una differenza di fase φ che dipende dagli indici no ed ne e dalla
lunghezza L della lamina.
Lo stato di polarizzazione dell’onda viene quindi alterato
2π
(n e − n o )L
Φ=
λ
Luigi Zeni DII-SUN Optoelettronica
Lamine a mezz’onda e a quarto d’onda
λ
L=
2(n e − n o )
Luigi Zeni DII-SUN Optoelettronica
L=
λ
4(n e − n o )
Compensatore Soleil-Babinet
Il compensatore consente di ottenere un ritardo variabile φ tra onda
ordinaria e onda straordinaria
2π
(n e − n o )(D − d )
Φ=
λ
I due cunei di quarzo scorrono l’uno sull’altro, variando lo spessore d,
e sono appoggiati su una lamina di quarzo di spessore D con asse ottico
ortogonale a quello dei cunei.
Luigi Zeni DII-SUN Optoelettronica
Prisma di Wollaston
Il prisma di Wollaston consente di ottenere da un’onda con polarizzazione
arbitraria due onde, con polarizzazioni lineari e ortogonali, divergenti di
un angolo che può variare da 15° a 45° a seconda di come è realizzato il
dispositivo (materiale ed angolo del prisma).
Luigi Zeni DII-SUN Optoelettronica
Attività ottica
Alcune sostanze, tra cui il quarzo e le soluzioni acquose di zucchero o
altre molecole organiche, ruotano il piano di polarizzazione di un’onda
linearmente polarizzata che le attraversa.
L’angolo di rotazione aumenta con la distanza percorsa (per il quarzo lo
incremento è di circa 17° per mm a 650nm).
Se la rotazione avviene in senso orario la sostanza è detta destrogira
altrimenti levogira.
Il quarzo può essere levogiro o destrogiro a seconda della forma cristallina
Luigi Zeni DII-SUN Optoelettronica
Effetto Elettro-Ottico
L’effetto elettro-ottico (E-O) è la variazione dell’indice di rifrazione
dei materiali per effetto di un campo elettrico esterno.
Un campo elettrico può trasformare un materiale isotropo in anisotropo.
Rappresentando l’indice di rifrazione in funzione del campo esterno
mediante una serie di Taylor si ha:
n ( E ) = n + a 1E + a 2 E 2 + ⋅ ⋅ ⋅
I coefficienti a1 e a2 sono chiamati rispettivamente coefficiente E-O
lineare e coefficiente E-O del secondo ordine.
•Le variazioni dovute al termine lineare sono dette Effetto Pockels
•Le variazioni dovute al termine quadratico sono dette Effetto Kerr
Luigi Zeni DII-SUN Optoelettronica
Effetto Pockels
L’effetto Pockels si manifesta solo nei cristalli non centrosimmetrici.
Ad esempio il cloruro di sodio ed il silicio sono centrosimmetrici e
non presentano effetto Pockels mentre l’arseniuro di gallio è non
centrosimmetrico e presenta effetto Pockels
∆n = a1E
L’effetto Pockels si può comprendere in maniera intuitiva immaginando
che il campo elettrico applicato deforma l’ellissoide degli indici e/o
modifica i valori di n1, n2 e n3.
Un materiale isotropo, il cui ellissoide è una sfera, si trasforma in
anisotropo oppure un materiale uniassico diventa biassico.
Ad esempio l’arseniuro di gallio (GaAs), che è un cristallo isotropo,
diventa birifrangente oppure cristalli come il KDP (KH2PO4), l’ADP
(AlH2PO4) e il niobato di litio (LiNbO3) che sono uniassici, subiscono
modifiche dell’ellissoide.
Luigi Zeni DII-SUN Optoelettronica
Effetto Pockels
a)
Assenza di campo elettrico applicato n1=n2=no
b, c) Campo elettrico applicato parallelamente all’asse y
Luigi Zeni DII-SUN Optoelettronica
Effetto Pockels
Nel niobato di litio, che è un cristallo molto usato in optoelettronica,
l’applicazione di un campo elettrico Ey parallelo all’asse principale
y induce birifrangenza nel senso che le onde che si propagano lungo
l’asse ottico (z) polarizzate linearmente lungo x e y vedono due
indici diversi n’1 e n’2 invece di vedere no
1 3
n ≈ n o + n o r22 E y
2
'
1
1 3
n ≈ n o − n o r22 E y
2
'
2
Dove r22 è una costante, chiamata coefficiente di Pockels, che dipende
dal materiale. In generale rij sono le componenti del tensore elettro-ottico
che lega le variazioni degli indici al campo esterno.
3
Luigi Zeni DII-SUN Optoelettronica
∆ i = ∑ rijE j
j=1
Tensore Elettro-ottico per LiNbO3 e KDP
∆1 r11 r12
∆ r
2 21 r22
∆ 3 r31 r32
=
∆ 4 r41 r42
∆ 5 r51 r52
∆ 6 r61 r62
r13
r23
E x
r33
⋅ E y
r43
E z
r53
r63
Per il KDP sono diversi da zero solo
due termini e valgono, per λ = 546nm:
r41 = 8.8 ⋅10 −12 m / V
r63 = 10.5 ⋅10 −12 m / V
Per il Niobato di Litio sono diversi da zero solo quattro termini e
valgono, per λ = 500nm:
r13 = 8.6 ⋅10 −12 m / V r22 = 3.4 ⋅10 −12 m / V
r33 = 30.8 ⋅10 −12 m / V r51 = 28 ⋅10 −12 m / V
Luigi Zeni DII-SUN Optoelettronica
Effetto Pockels trasversale
Si parla di effetto Pockels trasversale quando il campo elettrico
esterno è applicato ortogonalmente alla direzione di propagazione
della luce. Per il niobato di litio si ha:
2πL
1 3
2πL
1 3
φ1 =
φ2 =
n o + n o r22 E y
n o − n o r22 E y
2
λ
2
λ
2πL 3
2π 3 L
Dipende dal rapporto
n o r22 E y =
n o r22 V
∆φ = φ1 − φ 2 =
d’aspetto
d
λ
λ
Luigi Zeni DII-SUN Optoelettronica
Effetto Pockels longitudinale
Si parla di effetto Pockels longitudinale quando il campo elettrico
esterno è applicato lungo la direzione di propagazione della luce.
Per il KDP si ha:
2π 3
2πL 3
2π 3 L
n o r63 V
n o r63 E z =
n o r63 V =
∆φ = φ1 − φ 2 =
L
λ
λ
λ
Luigi Zeni DII-SUN Optoelettronica
Non dipende dal rapporto
d’aspetto
Modulatore con cella di Pockels
Utilizzando due polarizzatori con assi di trasmissione posti a 90° ed
una cella di Pockels si può realizzare un modulatore di intensità
controllato in tensione
La tensione corrispondente al massimo di intensità è quella per cui il
cristallo si comporta come una lamina a mezz’onda ed è detta tensione
di π o Vλ/2
Luigi Zeni DII-SUN Optoelettronica
Effetto Kerr
In un mezzo isotropo il campo elettrico trasforma la sfera degli indici
in un ellissoide, inducendo birifrangenza
Se la lunghezza è L e lo spessore è d si ha:
∆n = λKE 2z
2π∆n
2πλKE 2z
2πLKV 2
∆φ =
L=
L=
2
λ
λ
d
Luigi Zeni DII-SUN Optoelettronica
K è il coefficiente
di Kerr. Per il vetro:
K=3.10-15m/V2
Effetto Acusto-Ottico
L’effetto acusto-ottico consiste nella modifica delle proprietà ottiche,
ad esempio l’indice di rifrazione, di un mezzo per effetto di un’onda
acustica. E’ governato dal tensore elasto-ottico del mezzo
Il fascio diffratto subisce
uno shift Doppler pari alla
frequenza dell’onda acustica
viaggiante
Modulazione dell’indice di rifrazione con un’onda acustica di periodo Λ
Luigi Zeni DII-SUN Optoelettronica
2Λsinθ = λ / n
Condizione di Bragg
Effetto Magneto-Ottico
L’effetto magneto-ottico (effetto Faraday) consiste nella rotazione
del piano di polarizzazione di un’onda lanciata in un mezzo in
presenza di un campo magnetico parallelo alla sua direzione di
propagazione.
θ = ϑBL
L è la lunghezza del cammino, B è l’intensità del campo magnetico e
ϑ è la cosiddetta costante di Verdet del materiale.
E’ come se il materiale diventasse otticamente attivo e l’angolo di
rotazione dipende dalla direzione del campo magnetico, quindi se il
fascio torna su se stesso la rotazione si cumula e l’angolo complessivo
raddoppia.
Ad esempio un campo magnetico di 0.1T causa una rotazione di 1°
nell’attraversamento di una barra di vetro di 20mm
Luigi Zeni DII-SUN Optoelettronica
Isolatore ottico di Faraday
L’effetto Faraday si può utilizzare nella realizzazione di un isolatore
ottico, cioè di un componente che serve ad arrestare le onde riflesse.
Progettando opportunamente il componente, il piano di polarizzazione
della luce che torna verso la sorgente risulta ruotato di 90° ed essa viene
fermata dal polarizzatore.
Luigi Zeni DII-SUN Optoelettronica