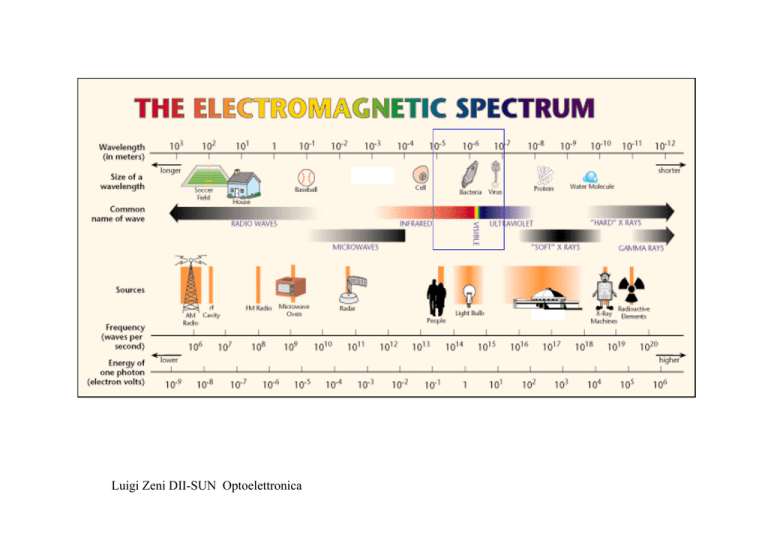
Luigi Zeni DII-SUN Optoelettronica
Equazioni di Maxwell
r
r
∂B
∇×E = −
∂t
r
r ∂D r
+J
∇×H =
∂t
r
∇⋅B = 0
r
∇⋅D = ρ
r
r
D = εE
r
B = µH
r
r
J = σE
ε : costante dielettrica
µ : permeabilità magnetica
σ : conducibilità elettrica
Luigi Zeni DII-SUN Optoelettronica
Dualismo onda-particella
Una particella di energia E e quantità di moto (impulso) p è descritta
da un’onda di frequenza f e costante di propagazione k secondo le
relazioni di Einstein - de Broglie:
ω
2
Ε = hf = h
= mc
2π
h
h
p=
k=
2π
λ
h: Costante di Planck
c: Velocità della luce
m: Massa
Luigi Zeni DII-SUN Optoelettronica
Equazione di Schrödinger
r
2
r
r
∂Ψ ( r , t ) h
2
jh
=
∇ Ψ ( r , t ) − UΨ ( r , t )
∂t
2m
r 2 r
r
r Probabilità di trovare la particella
Ψ ( r , t ) d r dt = P( r , t )d r dt in un intorno del punto r in un
intorno dell’istante t
∫
r 2 r
Ψ ( r , t ) d r dt = 1
r
t,r
Ψ è la funzione d’onda di una particella di massa m sottoposta ad
un potenziale U.
h è la costante di Planck razionalizzata pari a h/(2π).
Luigi Zeni DII-SUN Optoelettronica
Definizioni e grandezze
h = 6.626 ⋅10 −34 [Joule ⋅ s]
ε 0 = 8.842 ⋅10 −12 [Farad / m ]
µ 0 = 1.256 ⋅10 −6 [Henry / m ]
µ
ε
Impedenza del mezzo
n=
εµ
= ε rµ r
ε 0µ 0
Indice di rifrazione del mezzo
c=
1
= 3 ⋅108 m / s
ε 0µ 0
Velocità della luce nel vuoto
ζ=
v=
1
c
=
εµ n
Luigi Zeni DII-SUN Optoelettronica
Velocità della luce nel mezzo
Equazione delle onde in un mezzo
omogeneo e isotropo
r
2
r
∂
E
2
∇ E − µε 2 = 0
∂t
Assumendo per i campi una dipendenza temporale del tipo:
e
jω t
=e
j( 2 πf )t
Si ottiene:
r
r
∇2E + k 2E = 0
2π
⎛ 2π ⎞
k = k 0n =
n = ⎜ f ⎟n
λ
⎝ c ⎠
Luigi Zeni DII-SUN Optoelettronica
Costante di propagazione o
numero d’onda
Onde elettro-magnetiche (EM) piane
(
E x = E 0 cos ωt − kz + φ0
(
φ = ωt − kz + φ 0
Luigi Zeni DII-SUN Optoelettronica
)
)
Fase dell’onda
Velocità di fase
(
)
φ = ωt − kz + φ0 = cos tan te
Derivando rispetto al tempo si ha la velocità di fase:
dz ω 2πf
v=
= =
= fλ
dt k 2π
λ
La velocità di fase rappresenta lo spostamento per unità
di tempo del generico valore dell’ampiezza del campo
Luigi Zeni DII-SUN Optoelettronica
Onde elettro-magnetiche piane
Luigi Zeni DII-SUN Optoelettronica
Onda EM piana generica
Luigi Zeni DII-SUN Optoelettronica
Esempi di onde elettro-magnetiche
E = E 0 cos(ωt − kz )
Luigi Zeni DII-SUN Optoelettronica
(
r r
E0
E=
cos ωt − k ⋅ r
r
)
Esempi di onde elettro-magnetiche
Può originare da una sorgente estesa con una certa direttività
Luigi Zeni DII-SUN Optoelettronica
Fascio Gaussiano
La soluzione della equazione delle onde assumendo
una componente del campo del tipo
~
− jkz
E = Ψ (x , y, z )e
~
con Ψ funzione debolmente dipendente da z, si scrive:
⎧ ⎡
k 2
2
E = exp ⎨− j⎢P +
x +y
2q
⎩ ⎣
(
Luigi Zeni DII-SUN Optoelettronica
⎤⎫
⎥ ⎬ exp(− jkz )
⎦⎭
)
Fascio Gaussiano
I parametri P e q sono funzioni di z e soddisfano le relazioni:
dP
j
=−
dz
q
dq
=1
dz
λ
1
1
=
−j
q R (z)
πW (z) 2
Ponendo:
e
λ
1
= −j
2
q0
πW0
q0 rappresenta il valore di q per R=∞ si ha:
2
πW0
q= j
+z
λ
Luigi Zeni DII-SUN Optoelettronica
legge di propagazione del raggio
di curvatura complesso del fascio
Fascio Gaussiano
Si ottiene:
2 W (z) = 2 W0
⎛ λz ⎞
⎟
1 + ⎜⎜
2 ⎟
⎝ πW0 ⎠
⎡ ⎛ πW 2 ⎞ 2 ⎤
0
⎟⎟ ⎥
R (z) = z ⎢1 + ⎜⎜
⎢⎣ ⎝ λz ⎠ ⎥⎦
2
(W (0) = W0 ) Spot size
(R (0) = ∞ )
Raggio di curvatura
2 ⎞
⎛
⎛ λz ⎞ ⎟
⎜
−1 ⎛ λz ⎞
⎟ − tg ⎜⎜
⎟
P(z) = − j ln⎜ 1 + ⎜⎜
2 ⎟ ⎟
2 ⎟
πW0 ⎠ ⎟
πW0 ⎠
⎜
⎝
⎝
⎠
⎝
Luigi Zeni DII-SUN Optoelettronica
Fascio Gaussiano
Infine:
⎧⎪ ⎡
W0
k 2
−1 ⎛ λz ⎞
2
⎟
⎜
x
y
E=
exp ⎨− j⎢kz − tg ⎜
+
+
2 ⎟
W
2R
W (z)
π
⎪⎩ ⎣
0 ⎠
⎝
(
⎤ ⎫⎪
⎛ x 2 + y2 ⎞
⎟
⎥ ⎬ exp⎜⎜ −
2 ⎟
⎝ W (z) ⎠
⎦ ⎪⎭
)
Il fascio si attenua lungo z a causa del fattore 1/W(z) ed in direzione
radiale con profilo Gaussiano. Si definiscono:
⎛ πW02 ⎞
⎟⎟
Z R = ⎜⎜
⎝ λ ⎠
⎛ λ
θ0 ≅ tg (θ0 ) = ⎜⎜
⎝ πW0
⎞
W (z)
⎟⎟ = lim
⎠ z →∞ z
ZR viene detta “lunghezza di Rayleigh” e rappresenta la distanza
dall’origine entro la quale il fascio si considera collimato mentre θ0 è
detto “divergenza in campo lontano” del fascio
Luigi Zeni DII-SUN Optoelettronica
Fascio Gaussiano
Il minimo raggio del fascio W0 è detto “WAIST” del fascio e
rappresenta il punto in cui il fronte d’onda è piano cioè R=∞
Luigi Zeni DII-SUN Optoelettronica
Pacchetto d’onda
Due o più onde di frequenza leggermente diversa che si propagano nella
stessa direzione danno luogo al cosiddetto “pacchetto d’onda” il cui
inviluppo viaggia alla velocità di gruppo
Luigi Zeni DII-SUN Optoelettronica
Velocità di gruppo
E x (z, t ) = E 0 cos[(ω − δω)t − (k − δk )z ] + E 0 cos[(ω + δω)t − (k + δk )z ]
Dalle formule di prostaferesi si ha:
E x (z, t ) = 2E 0 cos[(δω)t − (δk )z ]cos[ωt − kz ]
Cioè un’onda a frequenza ω che si propaga nella direzione z la cui
ampiezza è modulata sinusoidalmente a frequenza δω. Un punto di
ampiezza generica per il quale (δω)t − (δk )z è costante, viaggia
alla velocità
dz δω
=
dt δk
dω
Ovvero, alla velocità di gruppo v g =
dk
Luigi Zeni DII-SUN Optoelettronica
Propagazione in un mezzo dispersivo
In un mezzo dispersivo di indice di rifrazione n(λ), per un
pacchetto d’onda di frequenza centrale ω, si ha k = n(2π/λ), quindi:
ω
2π
k=n
=n
c
λ
Differenziando si ottiene:
2π
2πn
dω
ω
n + dn
dk =
dn − 2 dλ =
λ
λ
c
c
dω ⎛ ω dn ⎞ c c ω dn
= ⎜1 −
⎟ = −
dk ⎝ c dk ⎠ n n n dk
Luigi Zeni DII-SUN Optoelettronica
Propagazione in un mezzo dispersivo
dk 2π 2π dλ
=
− 2 n
dn λ λ dn
dω c ω
λ dn
= −
dk n n 2π(λ (dn ) − n (dλ ) )
2
dω
=
dk
c
= vg
⎛ dn ⎞
n − λ⎜ ⎟
dλ ⎠
Luigi Zeni DII-SUN Optoelettronica ⎝
Velocità di gruppo
nel mezzo
Indice di gruppo di un mezzo dispersivo
Si definisce indice di gruppo la seguente grandezza:
dn
Ng = n − λ
dλ
Per cui la velocità di gruppo nel mezzo si scrive:
c
vg =
Ng
Che richiama l’espressione della velocità di fase nel mezzo:
c
v =
Luigi Zeni DII-SUN Optoelettronica
n
Indice di rifrazione e di gruppo per la silice
(SiO2)
Per λ=1µm si ha:
v=c / n = 2.069 108 m/s
vg = c / Ng = 2.055 108 m/s
Luigi Zeni DII-SUN Optoelettronica
Irradianza e vettore di Poynting
c
E x = By
n
La densità totale di energia elettromagnetica è la somma
dell’energia associata al campo elettrico e di quella associata
al campo magnetico:
1
1 2
2
2
ε0ε r E x +
By = ε0ε r E x
2
2µ 0
Luigi Zeni DII-SUN Optoelettronica
Irradianza e vettore di Poynting
Il flusso di energia per unità di tempo e di area sarà quindi:
(
v∆t )A (ε 0 ε r E
S=
A∆t
2
x
)= c ε ε E
n
0 r
2
2
x
⎛c⎞
= ⎜ ⎟ E x By
⎝n⎠
In generale, per un mezzo isotropo, l’energia fluisce nella direzione
di propagazione dell’onda e si ha:
r ⎛ c ⎞2
r r
S = ⎜ ⎟ ε 0ε r E × B
⎝n⎠
S è detto vettore di Poynting e la sua ampiezza è detta irradianza o
intensità e rappresenta la densità di potenza (flusso di potenza per
unità di area)
Luigi Zeni DII-SUN Optoelettronica
Riflessione e rifrazione in mezzi
isotropi e omogenei
Luigi Zeni DII-SUN Optoelettronica
Legge di Snell
La direzione di propagazione dell’onda incidente e la normale alla
interfaccia tra i due mezzi definiscono il piano di incidenza al quale
appartengono anche i vettori d’onda dell’onda riflessa e di quella
trasmessa
n1sin (θi ) = n 2sin (θ t )
θi = θ r
se
n1 < n 2 ⇒ θ t < θi
se
n1 > n 2 ⇒ θ t > θi
Luigi Zeni DII-SUN Optoelettronica
Riflessione interna totale (TIR)
θ t = 90°
⎛ n2 ⎞
⇒ θi = θc = sin ⎜⎜ ⎟⎟
⎝ n1 ⎠
−1
Oltre l’angolo critico non c’è potenza trasmessa ma esiste un’onda
evanescente che si propaga lungo l’interfaccia e si attenua
rapidamente allontanandosi dall’interfaccia
Luigi Zeni DII-SUN Optoelettronica
Riflessione interna totale
Oltre l’angolo critico, l’angolo di trasmissione diventa immaginario
e la componente del vettore d’onda normale all’interfaccia è anche
essa immaginaria
sin θ t > 1
⇒ cos θ t = 1 − sin 2 θ t = ± j sin 2 θ t − 1
2
⎛ n1
⎞
kt ⊥ = kt cos θ t = ± jk ⎜⎜ sin θ i ⎟⎟ − 1
⎝ n2
⎠
n1
kt|| = kt sin θ t = k sin θ i
n2
Luigi Zeni DII-SUN Optoelettronica
Profondità di penetrazione
L’onda evanescente avrà la seguente espressione:
(
Et = E t 0 e
r r
j ωt − k t ⋅ r
1
δ=
kt ⊥
) = E e j (ωt − kt|| z )e − kt ⊥ y
t0
Profondità di penetrazione [cm]
Luigi Zeni DII-SUN Optoelettronica
Spostamento di Goos-Haenchen
In condizioni di riflessione totale l’onda riflessa appare spostata
lateralmente di una quantità ∆z come se l’interfaccia si trovasse
all’interno del mezzo ad una profondità δ
∆z = (2δ )tgθi
Luigi Zeni DII-SUN Optoelettronica
Riflessione interna “frustrata” (FTIR)
Se, ad una distanza dall’interfaccia dell’ordine di δ, c’è una discontinuità
cioè un mezzo di indice diverso (n3) può esistere un’onda non evanescente
nel mezzo di indice n3 e si parla di riflessione interna totale frustrata
(Frustrated Total Internal Reflection -FTIR-)
In condizioni di FTIR si parla di “tunneling ottico” perché esiste un’onda
trasmessa dove l’ottica geometrica lo proibisce
Luigi Zeni DII-SUN Optoelettronica
Esempio di applicazione della FTIR
Divisore di fascio
(Cubo beam-splitter)
Luigi Zeni DII-SUN Optoelettronica
Polarizzazione
Per il calcolo dell’ampiezza e della fase delle onde riflesse e
trasmesse occorre tener conto dello stato di polarizzazione.
Come è noto lo stato di polarizzazione di un’onda elettromagnetica può
essere:
Lineare: l’estremità del vettore campo elettrico oscilla lungo una linea retta
Circolare: l’estremità del vettore campo elettrico descrive una circonferenza
Ellittico: l’estremità del vettore campo elettrico descrive una ellisse
Random: l’estremità del vettore campo elettrico si muove in maniera casuale
Nell’ultimo caso si parla di luce non-polarizzata
Lo stato di polarizzazione di un onda può essere modificato mediante
opportuni componenti (polarizzatori, lamine di ritardo, etc)
Luigi Zeni DII-SUN Optoelettronica
Polarizzazione
Indicando con (x,y) le coordinate dell’estremità del vettore campo
elettrico nel piano ortogonale alla direzione di propagazione
dell’onda si ha:.
r
E = E x cos(ωt + α) x̂ + E y cos(ωt + β) ŷ
x = E x cos(ωt + α)
y = E y cos(ωt + β)
Il luogo descritto dal punto di coordinate (x,y) al passare del tempo
definisce lo stato di polarizzazione
Luigi Zeni DII-SUN Optoelettronica
Polarizzazione
Indicando con (x,y) le coordinate dell’estremità del vettore campo
elettrico nel piano ortogonale alla direzione di propagazione
dell’onda si ha:.
α = β + nπ
π
α =β+
2
π
α ≠β+
2
⇒
y=
Ey
Ex
x
Ex = Ey = E
e / o Ex ≠ Ey
⇒
⇒
x 2 + y2 = E2
Ax 2 + By 2 + Cxy = D
Studiando quindi il comportamento delle componenti Ex ed Ey, di seguito
indicate con E⊥ ed E|| con riferimento al piano di incidenza,è possibile seguire lo
stato di polarizzazione dopo riflessioni e trasmissioni
Luigi Zeni DII-SUN Optoelettronica
Formule di Fresnel
θ i < θc
Luigi Zeni DII-SUN Optoelettronica
θ i > θc
Formule di Fresnel
Nell’ipotesi in cui la permeabilità magnetica dei due mezzi è
identica (µ1 = µ2) i coefficienti di riflessione e trasmissione, per
le due componenti linearmente polarizzate del campo elettrico,
sono:
n1 cos θi − n 2 cos θ t
r⊥ =
;
n1 cos θi + n 2 cos θ t
2n1 cos θi
t⊥ =
n1 cos θi + n 2 cos θ t
1 + r⊥ = t ⊥
n1 cos θ t − n 2 cos θi
;
r|| =
n 2 cos θi + n1 cos θ t
n2
t || + r|| = 1
n1
Luigi Zeni DII-SUN Optoelettronica
2n1 cos θi
t || =
n 2 cos θi + n1 cos θ t
Formule di Fresnel
Oltre l’angolo limite il modulo dei coefficienti di riflessione è
unitario mentre la fase è:
⎛ n2 ⎞
sin θi − ⎜⎜ ⎟⎟
⎞
⎛1
⎝ n1 ⎠
tg⎜ Φ ⊥ ⎟ = −
cos θi
⎠
⎝2
2
2
⎛ n2 ⎞
sin θi − ⎜⎜ ⎟⎟
⎝ n1 ⎠
2
π⎞
⎛1
tg⎜ Φ || + ⎟ = −
2⎠
⎝2
Luigi Zeni DII-SUN Optoelettronica
2
⎛ n2 ⎞
⎜⎜ ⎟⎟ cos θi
⎝ n1 ⎠
2
Formule di Fresnel
θp : Angolo di polarizzazione o angolo di Brewster
Luigi Zeni DII-SUN Optoelettronica
Calcolo dell’angolo di Brewster
Se, per polarizzazione parallela, la direzione di propagazione
dell’onda trasmessa è ortogonale a quella dell’onda riflessa cioè:
θt = π/2 - θi non c’è onda riflessa perché i dipoli elementari nel
mezzo n2 non possono irradiare in direzione ortogonale al campo
elettrico che mette in movimento le cariche
⎛π
⎞
sin ⎜ − θi ⎟
n1 sinθ t
1
2
⎝
⎠
=
=
=
n 2 sinθi
sinθi
tgθi
⇓
n2
θ p = tg
n1
−1
Luigi Zeni DII-SUN Optoelettronica
Formalismo di Jones
Per studiare la variazione dello stato di polarizzazione di un’onda
che subisce riflessione o trasmissione è possibile utilizzare il
formalismo di Jones cioè la rappresentazione mediante matrici
2X2 dei diversi componenti ottici
r
⎡ E x e j Φ x ⎤ jω t
E IN = ⎢
jΦ y ⎥ e
⎢⎣ E y e ⎥⎦
⎡ J11
J=⎢
⎣J 21
J12 ⎤
⎥
J 22 ⎦
Luigi Zeni DII-SUN Optoelettronica
r
⎡ J11
E OUT = ⎢
⎣J 21
jΦ x
⎡
J12 ⎤ E x e ⎤
⋅⎢
jΦ y ⎥
⎥
J 22 ⎦ ⎢⎣ E y e ⎥⎦
Matrici di Jones notevoli
J Px
Jλ
⎡1 0⎤
=⎢
⎥
⎣0 0 ⎦
Polarizzatore x
Polarizzatore y
⎡
= ⎢e
⎢
⎣ 0
⎡ − j π4
= ⎢e
⎢
⎣ 0
π
−j
2
2
J Py
⎡0 0 ⎤
=⎢
⎥
0
1
⎣
⎦
⎤
0⎥
π
j ⎥
e 2⎦
Lamina a λ/2
Luigi Zeni DII-SUN Optoelettronica
Jλ
4
⎤
0⎥
π
j ⎥
e 4⎦
Lamina a λ/4
Strati anti-riflesso e specchi dielettrici
E’ possibile utilizzare uno o più strati dielettrici per minimizzare il
coefficiente di riflessione facendo interferire distruttivamente le onde
AeB
⎛ λ ⎞
⎛ 2πn 2 ⎞
⎟⎟
m = 1,3,5...
⎜
⎟2d = mπ ovvero d = m⎜⎜
⎝ λ ⎠
⎝ 4n 2 ⎠
n2 =
(n1n 3 )
Luigi Zeni DII-SUN Optoelettronica
Specchi dielettrici
Utilizzando diversi strati dielettrici a λ/4 si può ottenere un
assegnato andamento della riflettanza, definita come modulo al
quadrato del coefficiente di riflessione, realizzando i cosiddetti
specchi dielettrici
Luigi Zeni DII-SUN Optoelettronica
Interferometro Fabry-Perot
E’ costituito da due specchi piani e paralleli di riflettanza R. Alla
risonanza le onde che viaggiano nelle due direzioni interferiscono
costruttivamente. La condizione di risonanza e:
⎛λ⎞
⎛ c ⎞
m⎜ ⎟ = L
ν = m⎜
⎟ = mν f m = 1,2,3...
⎝2⎠
⎝ 2L ⎠
Le lunghezze d’onda che soddisfano la condizione di risonanza
definiscono i modi della cavità
Luigi Zeni DII-SUN Optoelettronica
Interferometro Fabry-Perot
Le corrispondenti frequenze νmsono le frequenze di risonanza della
cavità Fabry-Perot e νf è detto “free spectral range” o frequenza di
battimento fondamentale. Al crescere della riflettanza (quindi perdite
minori) l’energia si concentra intorno alle frequenze di risonanza.
I0
I Cavità =
Si calcola considerando la
2
2
(1 − R ) + 4Rsin (kL )
somma di infinite riflessioni
I0
I max =
kL = mπ
2
(1 − R )
νf
Larghezza spettrale (FWHM)
δν =
F
π R
Finesse
F=
1− R
Luigi Zeni DII-SUN Optoelettronica
Intensità trasmessa da un Fabry-Perot
I trasmessa = I incidente
(1 − R )2
(1 − R )2 + 4Rsin 2 (kL )
Un Fabry-Perot con elevata finesse realizza un filtro ottico a banda
molto stretta.
Si noti la dipendenza da k e quindi dall’indice di rifrazione in cavità.
Luigi Zeni DII-SUN Optoelettronica
Interferometro di Michelson
Specchio fisso
d1
50%
I0
d2
I t = I1 + I 2 + 2 I1I 2 cos(∆Φ )
It
Intensità media in uscita
4π
(n1d1 − n 2d 2 )
∆Φ = 2k1d1 − 2k 2 d 2 =
λ
Un interferometro di Michelson presenta in uscita, al variare di d2,
massimi e minimi (frange di interferenza) finché ∆φ è deterministico.
Luigi Zeni DII-SUN Optoelettronica
Interferometro di Michelson
Se I1 = I2 = I0/4, cioè l’interferometro è perfettamente bilanciato in
potenza, si ha:
I0
I t = (1 + cos(∆Φ ))
2
In generale si definisce “visibilità” delle frange il parametro:
V=
I t max − I t min
I t max + I t min
2 I1I 2
=
I1 + I 2
0 ≤ V ≤1
La visibilità è massima per l’interferometro bilanciato in potenza
Luigi Zeni DII-SUN Optoelettronica
Lunghezza e tempo di coerenza
Nel momento in cui ∆φ diventa una variabile aleatoria si ottiene in
uscita un valore costante di intensità pari a I.
Si definisce lunghezza di coerenza l la differenza di lunghezza tra i
due bracci dell’interferometro oltre cui non si osserva più variazione
di intensità in uscita. Si definisce tempo di coerenza ∆t = l/c
Il concetto di tempo di coerenza è legato alla capacità di una sorgente
di emettere un treno d’onda di una certa durata senza salti di fase ed è
quindi legato alla banda dal teorema di Fourier
⎛ t ⎞
E( t ) = E 0sin (ω0 t − k 0 z )Π⎜ ⎟
Treno d’onda
⎝ ∆t ⎠
1
∆ν ≈
∆t
Larghezza spettrale (banda)
2
λ0
∆λ ≈ ∆ν
c
Luigi Zeni DII-SUN Optoelettronica
Lunghezza e tempo di coerenza
(a) Sinusoide ideale
(b) Treno d’onda
(c) Segnale a larga banda
Luigi Zeni DII-SUN Optoelettronica
Coerenza spaziale di una sorgente
Si definisce coerenza spaziale di una sorgente estesa la coerenza
tra le onde radiate da diversi punti della sorgente stessa
Luigi Zeni DII-SUN Optoelettronica
Principio di Huygens-Fresnel
Consente di descrivere il campo come sovrapposizione di onde sferiche
radiate dai punti investiti dalla radiazione
Luigi Zeni DII-SUN Optoelettronica
E ' ( x ' , y ' , z ' ) − jkr
e dV
E( x , y, z) ∝ ∫
r
V
Diffrazione da una apertura
Diffrazione di Fresnel:
lo schermo è “vicino” all’apertura
Diffrazione di Fraunhofer: lo schermo è “lontano” dall’apertura
La condizione “vicino” o “lontano” è legata alla dimensione massima
della apertura D ed alla lunghezza d’onda
πD 2
z ≅ r >>
λ
Definizione di zona di Fraunhofer
Si può facilmente dimostrare, tramite il principio di Huygens-Fresnel,
che il campo in zona di Fraunhofer è proporzionale alla trasformata di
Fourier della distribuzione di campo sull’apertura
Luigi Zeni DII-SUN Optoelettronica
Diffrazione di Fraunhofer da una fenditura
(
Luigi Zeni DII-SUN
[(
) ]
2
⎧⎪ sin 1 ka sinθ ⎫⎪
2
I(θ) ∝ I(0)⎨
= I(0)sinc 2 1 ka sinθ
⎬
2
⎪⎩ 1 2 ka sinθ ⎪⎭
y
mλ
I(θ) = 0 se
≅ sinθ =
m = ±1, ± 2,...
z
a
Optoelettronica
)
[(
) ]
Diffrazione di Fraunhofer da una
apertura rettangolare
[(
) ]
[(
) ]
I(θ, ρ) ∝ I(0)sinc 2 1 ka sinθ sinc 2 1 kb sinρ
2
2
mλ
sinθ =
a
I(θ, ρ) = 0 se
m = ±1, ± 2,...
mλ
sinρ =
b
Luigi Zeni DII-SUN Optoelettronica
Diffrazione di Fraunhofer da una
apertura circolare
Pattern di intensità
⎡ 2J1 (2kRsinθ) ⎤
I(θ) ∝ ⎢
⎥
J1: Funzione di Bessel 1a specie ordine 1
⎣ 2kRsinθ ⎦
d
λ
d: Raggio del disco principale di diffrazione
≅ sinθd = 1.22
z
2R
2
Luigi Zeni DII-SUN Optoelettronica
Potere risolutivo dei sistemi ottici
Due sorgenti diventano indistinguibili se il sistema ottico (occhio,
microscopio, telescopio, etc) dotato di apertura circolare di raggio
R forma un pattern di diffrazione dove i dischi di Airy si
sovrappongono
λ
sin (∆θ min ) = 1.22
λ
λn =
n
Luigi Zeni DII-SUN Optoelettronica
n
2R
n: indice di rifrazione del mezzo
Reticoli di diffrazione
Il reticolo di diffrazione più semplice è costituito da una sequenza
periodica di aperture in uno schermo. Il diagramma di intensità in
zona di Fraunhofer è costituito da una serie di massimi e minimi il
cui inviluppo è il diagramma di diffrazione della singola apertura.
Luigi Zeni DII-SUN Optoelettronica
Reticoli di diffrazione
Il diagramma di intensità in zona di Fraunhofer di un reticolo
costituito da N aperture rettangolari di lunghezza a e larghezza b
distanti d>>a l’una dall’altra disposte lungo la direzione dell’asse
y, ad una distanza z dal piano del reticolo stesso, è rappresentato da:
⎛ b ⎞
⎞ ⎡ sin (Nδ ) ⎤
2⎛ a
I(x, y ) ∝ sinc ⎜ x ⎟sinc ⎜ y ⎟ ⎢
⎥
⎝ λz ⎠
⎝ λz ⎠ ⎣ sinδ ⎦
y
π y
δ= d
≅ sinθ
z
λ z
2
y
z
I massimi si hanno per: d = mλ ⇒ y = mλ
z
d
z
Ampiezza alla base dei massimi:
∆ = 2λ
Nd
Luigi Zeni DII-SUN Optoelettronica
m = 0,±1,±2,..
Reticoli di diffrazione
In generale costituisce un reticolo qualsiasi perturbazione periodica
della ampiezza o della fase di un’onda o di entrambe.
Se l’onda incidente forma un angolo θi con la normale al reticolo si ha:
d(sinθ m − sinθi ) = mλ
Luigi Zeni DII-SUN Optoelettronica
m = 0,±1,±2,..
θm: posizione angolare dei massimi
Reticoli di Bragg
Si parla di reticoli di Bragg quando la perturbazione periodica si
sviluppa nel piano di incidenza dell’onda invece che ortogonalmente
ad esso
Variazione periodica
di indice di rifrazione
λ
2Λsinθ = m
n
m = ±1,±2,..
Luigi Zeni DII-SUN Optoelettronica
Condizione di Bragg