Cristalli e bande di energia
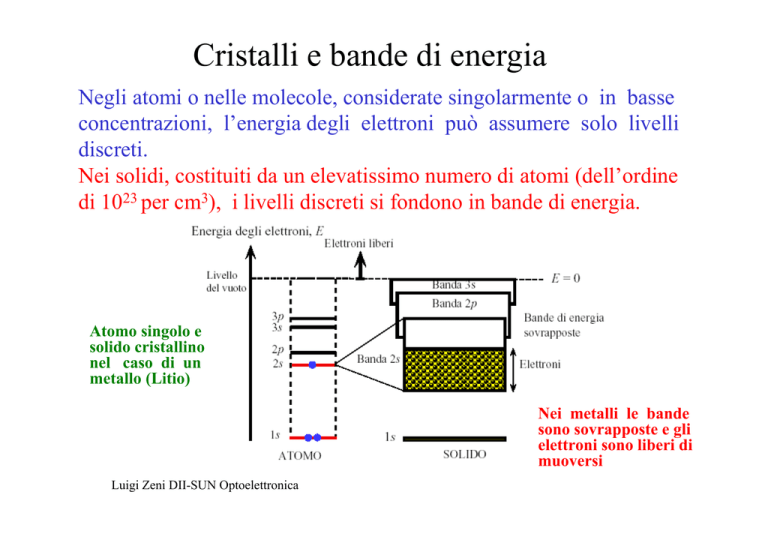
Negli atomi o nelle molecole, considerate singolarmente o in basse
concentrazioni, l’energia degli elettroni può assumere solo livelli
discreti.
Nei solidi, costituiti da un elevatissimo numero di atomi (dell’ordine
di 1023 per cm3), i livelli discreti si fondono in bande di energia.
Atomo singolo e
solido cristallino
nel caso di un
metallo (Litio)
Nei metalli le bande
sono sovrapposte e gli
elettroni sono liberi di
muoversi
Luigi Zeni DII-SUN Optoelettronica
Semiconduttori e bande di energia
Nei semiconduttori esistono due bande distinte, banda di valenza (VB)
e banda di conduzione (CB), separate da un intervallo di energia proibito
Eg (badgap). L’ampiezza χ della CB è detta affinità elettronica.
Cristallo di silicio e corrispondente diagramma a bande allo zero assoluto
Luigi Zeni DII-SUN Optoelettronica
Elettroni e lacune
Un elettrone (e-) che si trova in banda di conduzione si può trattare
come un elettrone libero purché gli venga assegnata una massa efficace
(me*) che tiene conto dell’interazione con il cristallo.
Per portare un elettrone dalla banda di valenza a quella di conduzione
occorre fornire una energia almeno pari a Eg.
A temperature superiori a 0K, un certo numero di elettroni si trova in
banda di conduzione (generazione termica).
Il “vuoto” lasciato dall’elettrone mancante nella banda di valenza viene
detto lacuna (h+) e può essere rappresentato come una particella con
carica positiva (pari alla carica dell’elettrone) che si può trattare come
una particella libera purché le venga assegnata una massa efficace (mh*)
che tiene conto dell’interazione con il cristallo.
Lo spostamento di una lacuna avviene quando un elettrone, appartenente
ad un legame covalente vicino, “salta” nella lacuna lasciando una nuova
lacuna al suo posto.
Luigi Zeni DII-SUN Optoelettronica
Fotogenerazione di coppie e- - h+
L’energia necessaria a portare un elettrone dalla banda di valenza a quella
di conduzione può essere fornita da un fotone di energia hν > Eg
Luigi Zeni DII-SUN Optoelettronica
Ricombinazione di coppie e- - h+
Quando un elettrone che si trova in banda di conduzione incontra una
lacuna in banda di valenza, trova di fatto uno stato permesso di energia
inferiore e lo occupa rilasciando l’energia in eccesso.
Questo processo viene detto ricombinazione delle coppie e- - h+.
L’energia in eccesso può essere rilasciata sotto varie forme, a secondo
del tipo di semiconduttore:
•Ricombinazione radiativa (Arseniuro di Gallio, Fosfuro di Indio, ..)
l’energia è rilasciata sotto forma di fotoni
•Ricombinazione non radiativa (Silicio, Germanio, ..)
l’energia è rilasciata sotto forma di vibrazioni reticolari (calore)
Entrambi i meccanismi, se consentiti, possono essere presenti contemporaneamente.
All’equilibrio termodinamico la velocità di generazione termica eguaglia quella di
ricombinazione.
Luigi Zeni DII-SUN Optoelettronica
Densità degli stati nei semiconduttori
Molte proprietà dei semiconduttori possono essere descritte considerando la
distribuzione statistica degli elettroni e delle lacune rispettivamente in banda di
conduzione e banda di valenza.
Si definisce la funzione g(E) che rappresenta la densità degli stati (DOS), cioè
il numero di stati elettronici in una banda per unità di energia e per unità di
volume.
La densità degli stati, in accordo con la meccanica quantistica, cresce con la
energia e fornisce informazioni solo sugli stati disponibili, non sulla effettiva
occupazione degli stessi.
g CB (E ) ∝ E − E c
In banda di conduzione
g VB (E ) ∝ E v − E
In banda di valenza
La effettiva probabilità di occupazione di uno stato è descritta mediante il modello
statistico di Fermi-Dirac
Luigi Zeni DII-SUN Optoelettronica
Statistica di Fermi-Dirac
La statistica di Fermi-Dirac, f(E), rappresenta la probabilità di trovare un elettrone
in uno stato quantistico di energia E:
1
f (E) =
E − EF
1 + exp
k BT
EF : Energia di Fermi
kB: Costante di Boltzmann
T: Temperatura assoluta
L’energia di Fermi è il livello cui compete una probabilità di occupazione pari a
0.5 e rappresenta, allo zero assoluto (T=0), il confine tra gli stati occupati e quelli
vuoti.
Inoltre, ogni variazione del livello di Fermi all’interno di un materiale implica
l’esistenza di una differenza di potenziale V e rappresenta, quindi, un lavoro per
l’elettrone: ∆EF = eV.
La probabilità di trovare una lacuna in uno stato quantistico di energia E è 1-f(E)
Luigi Zeni DII-SUN Optoelettronica
Concentrazione dei portatori
La effettiva concentrazione degli elettroni e delle lacune in un semiconduttore per
unità di energia è:
n E = g CB (E)f (E) ;
Luigi Zeni DII-SUN Optoelettronica
p E = g VB (E)(1 − f (E))
Concentrazione dei portatori
Il numero totale di elettroni in banda di conduzione e di lacune in banda di valenza
è calcolabile integrando nE e pE sulle rispettive bande:
n = ∫ g CB (E)f (E)dE ;
p = ∫ g VB (E)[1 − f (E)]dE
Ipotizzando che il livello di Fermi si trovi abbastanza lontano (alcuni kBT) dai bordi
delle bande, si è in presenza di semiconduttori non degeneri e la statistica di FermiDirac può essere approssimata dalla statistica di Boltzmann:
f (E) ≅ exp[− (E − E F ) / k BT ]
da cui si può mostrare che:
n = N c exp[− (E c − E F ) / k BT ];
dove:
p = N v exp[− (E F − E v ) / k BT ]
2πm k T
N c = 2
h
Luigi Zeni DII-SUN Optoelettronica
*
e B
2
32
2πm k T
; N v = 2
h
*
h B
2
32
Legge di azione di massa
Il prodotto delle concentrazioni dei portatori segue la legge di
azione di massa, valida ogniqualvolta il campione è al buio e
all’equilibrio termico
Eg
= n i2
np = N c N v exp −
k BT
Si noti che il prodotto delle concentrazioni dei portatori non dipende
dalla posizione del livello di Fermi ma solo dalla temperatura e dalle
proprietà del materiale.
La posizione del livello di Fermi dipende dal tipo di semiconduttore e
dalla presenza di eventuali impurità nel cristallo
Luigi Zeni DII-SUN Optoelettronica
Semiconduttori intrinseci
Un semiconduttore si dice intrinseco se si tratta di un cristallo puro. In tal caso la
concentrazione di elettroni eguaglia quella delle lacune:
n = p = ni
[(
→
)
]
[(
)
N c exp − E c − E Fi / k BT = N v exp − E Fi − E v / k BT
]
Da cui è possibile ricavare EFi,che indica il livello di Fermi intrinseco:
Nc
1
1
E Fi = E v + E g − (k BT ) ln
2
2
Nv
Il livello di Fermi intrinseco si trova quasi al centro del band-gap
in quanto Nc e Nv hanno valori comparabili.
Luigi Zeni DII-SUN Optoelettronica
Semiconduttori estrinseci
Introducendo in un semiconduttore una piccola quantità di atomi estranei (drogaggio),
si ottiene un semiconduttore estrinseco. Come drogante si usano atomi che rimpiazzano
quelli di semiconduttore ed hanno un elettrone in più (tipo n) o in meno (tipo p)
Drogaggio con Arsenico: tipo n (atomi donatori)
L’elettrone “in più “ si porta in banda di conduzione con la somministrazione di
0.05eV (è sufficiente l’energia termica a temperatura ambiente)
Luigi Zeni DII-SUN Optoelettronica
Semiconduttori estrinseci
Drogaggio con Boro: tipo p (atomi accettori)
L’atomo di boro presenta un elettrone “in meno “ rispetto al silicio per cui lascia un
legame covalente non saturo nel cristallo, cioè una lacuna.
E’ come se accettasse un elettrone dalla banda di valenza creando una lacuna che è
libera di svincolarsi dall’atomo di boro mediante somministrazione di 0.05eV
(è sufficiente l’energia termica a temperatura ambiente)
Luigi Zeni DII-SUN Optoelettronica
Semiconduttori estrinseci
a) Semiconduttore intrinseco: n=p=ni
b) Semiconduttore di tipo n : n > p (il livello di Fermi si sposta verso la CB)
c) Semiconduttore di tipo p : p > n (il livello di Fermi si sposta verso la VB)
Luigi Zeni DII-SUN Optoelettronica
Conducibilità elettrica
La conducibilità elettrica dipende, in generale, sia dagli elettroni sia dalle lacune:
σ = enµ e + epµ h
dove µe e µh sono le mobilità degli elettroni e delle lacune
mentre e=q è la carica dell’elettrone.
In un semiconduttore di tipo n, drogato con Nd atomi di drogante per cm3, la
concentrazione degli elettroni a temperatura ambiente è n≈Nd e quella delle
lacune si può ricavare dalla legge di azione di massa p=ni2/Nd , quindi:
n i2
σ = eN d µ e + e
µ h ≈ eN d µ e
Nd
In un semiconduttore di tipo p, drogato con Na atomi di drogante per cm3, la
concentrazione delle lacune a temperatura ambiente è p≈Na e quella degli
elettroni si può ricavare dalla legge di azione di massa n=ni2/Na , quindi:
n i2
σ=e
µ e + eN a µ h ≈ eN a µ h
Na
Luigi Zeni DII-SUN Optoelettronica
Portatori maggioritari e minoritari
In un semiconduttore di tipo n gli elettroni sono definiti portatori maggioritari e le
lacune portatori minoritari.
Si utilizza la seguente notazione:
n no
Concentrazione di elettroni all’equilibrio
p no
Concentrazione di lacune all’equilibrio
In un semiconduttore di tipo p le lacune sono definite portatori maggioritari e gli
elettroni portatori minoritari.
Si utilizza la seguente notazione:
n po
Concentrazione di elettroni all’equilibrio
p po
Concentrazione di lacune all’equilibrio
E’ possibile trasformare un semiconduttore da tipo n a tipo p e viceversa aggiungendo
opportunamente drogante (compensazione)
Luigi Zeni DII-SUN Optoelettronica
Semiconduttori degeneri
Normalmente il livello di drogaggio dei semiconduttori (1015-1018 cm-3) porta ad un
numero di elettroni in banda di conduzione o lacune in banda di valenza molto più
piccolo del numero degli stati disponibili. Ciò consente di ignorare il principio di
esclusione di Pauli e utilizzare la statistica di Boltzmann (n << Nc e p << Nv ).
Se il drogaggio è dell’ordine di 1019-1020 cm-3 si ha n ≈ Nc e p ≈ Nv e bisogna
utilizzare la statistica di Fermi-Dirac. Si parla allora di semiconduttori degeneri
e il loro comportamento è molto vicino a quello dei metalli.
Il livello di Fermi si trova in banda di conduzione, per il tipo n (fig. a), e in banda
di valenza, per il tipo p (fig. b)
N.B.
Non tutto il drogante è
ionizzato e non vale la
legge di azione di massa
Luigi Zeni DII-SUN Optoelettronica
Diagramma a bande in presenza di campo
Applicando un campo elettrico ad
un
semiconduttore il diagramma a
bande
risulta inclinato a causa della differenza
di potenziale che cresce da un estremo all’altro.
Il livello di Fermi varia di una quantità pari a
eV e scorre una corrente nel cristallo.
La concentrazione di elettroni resta costante e
quindi Ec - EF deve restare costante per cui CB,
CV ed EF restano paralleli.
Luigi Zeni DII-SUN Optoelettronica
Elettrone in una buca di potenziale
L’energia potenziale di un elettrone confinato in una buca di potenziale, di larghezza
spaziale L e altezza infinita, è quantizzata ed espressa da:
(
hk n )
=
2
En
nπ
; con k n =
2m e
L
n = 1,2,⋅ ⋅
La grandezza kn è il numero d’onda dell’elettrone (meve=hk/2π è l’impulso cioè il
prodotto della massa per la velocità dell’elettrone secondo la relazione di de Broglie).
L’energia cresce quadraticamente con il numero d’onda (andamento parabolico).
Il modello dell’elettrone nella buca è utilizzabile per i metalli dove si può considerare
l’energia potenziale costante in quanto gli elettroni sono praticamente liberi di
muoversi.
Nel caso dei semiconduttori la relazione tra energia e numero d’onda è più complessa
e richiede la soluzione dell’equazione di Schroedinger in presenza di un potenziale
periodico. L’impulso dell’elettrone legato viene chiamato momento del cristallo.
Luigi Zeni DII-SUN Optoelettronica
Funzioni d’onda di Bloch
La soluzione dell’equazione di Schroedinger fornisce le funzioni d’onda dell’elettrone
nel cristallo, periodiche come il potenziale, dette funzioni d’onda di Bloch:
ψ k ( x ) = U k ( x ) exp( jkx )
Luigi Zeni DII-SUN Optoelettronica
Diagramma E-k
Ogni funzione d’onda rappresenta uno stato di energia Ek e numero d’onda k.
L’andamento dell’energia in funzione del numero d’onda dipende dal materiale
semiconduttore considerato (è un insieme discreto di punti molto vicini)
Ogni punto del diagramma
è una possibile funzione d’onda
per l’elettrone nel cristallo
Nelle transizioni tra bande si deve
conservare l’energia e l’impulso
(momento)
Luigi Zeni DII-SUN Optoelettronica
Semiconduttori a bandgap diretto e indiretto
Si parla di semiconduttori a bandgap diretto se il minimo della banda di conduzione è
“allineato” con il massimo della banda di valenza.
Nei semiconduttori a bandgap diretto è possibile avere ricombinazione radiativa in
quanto il momento si conserva automaticamente e l’energia può essere portata via da
un fotone che presenta momento trascurabile.
Nei semiconduttori a bandgap indiretto la ricombinazione richiede l’interazione con
un centro di ricombinazione e avviene con emissione di un fonone.
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n
Si parla di omogiunzione p-n quando
un semiconduttore drogato con atomi
donatori viene posto in contatto con
uno (uguale) drogato con atomi
accettori.
Quando si utilizzano semiconduttori
di specie diversa si parla invece di
eterogiunzione.
All’equilibrio si instaura un campo
elettrico, generato dagli ioni di
drogante, che contrasta la diffusione
dei portatori annullando la corrente
N a Wp = N d Wn
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n
L’andamento del campo elettrico è
determinabile mediante il teorema di
Gauss e, nel caso di giunzione brusca,
presenta un profilo triangolare.
La differenza di potenziale che si
instaura ai capi della giunzione è detta
“potenziale built-in”
eN a Wp
eN d Wn
=−
ε
ε
1
eN a N d Wo2
Vo = − E o Wo =
2
2ε(N a + N d )
Eo = −
Wo = Wn + Wp
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n
L’espressione del “potenziale built-in” dipende dalla concentrazione del drogante,
dalla costante dielettrica del semiconduttore e dalla larghezza della zona di
svuotamento. Utilizzando la statistica di Boltzmann è possibile trovare una relazione
tra le concentrazioni dei portatori nelle regioni n e p, infatti esistendo tra i portatori
della stessa specie che si trovano ai due lati della giunzione una differenza di energia,
si può scrivere:
n 2 n1 = exp[− (E 2 − E1 ) / k BT ];
n po
n no
= exp(− eVo k BT )
p no
= exp(− eVo k BT )
p po
n i2
p po = N a ; p no =
Nd
Luigi Zeni DII-SUN Optoelettronica
p 2 p1 = exp[− (E1 − E 2 ) / k B T ]
k BT n no k BT p po
Vo =
ln
ln
=
e
e
p no
n po
k BT N a N d
Vo =
ln 2
e
ni
Giunzione p-n: Polarizzazione diretta
Applicando alla giunzione p-n una batteria con il polo positivo connesso al lato p e
quello negativo al lato n si parla di polarizzazione diretta e si ha un flusso di corrente
nel circuito
La differenza di potenziale applicata cade praticamente tutta sulla regione di carica spaziale
(SCL) poiché le regioni neutre sono ad elevata conducibilità, e abbassa la barriera di potenziale
built-in Vo, portandola a Vo-V. L’abbassamento della barriera provoca una diffusione di lacune
dal lato p a quello n e, similmente, una diffusione di elettroni dal lato n a quello p.
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n: Polarizzazione diretta
La diffusione di elettroni e lacune, rispettivamente nelle regioni neutre p e n, provoca
un leggero incremento della concentrazione dei portatori maggioritari per conservare
la neutralità.
La concentrazione di lacune al bordo esterno della regione di carica spaziale nel
lato n dipende dalla diffusione causata dall’abbassamento della barriera di
potenziale:
− e(Vo − V )
eV
p n (0) = p po exp
= p no exp
k
T
k
T
B
B
La concentrazione di elettroni al bordo esterno della regione di carica spaziale nel
lato p dipende dalla diffusione causata dall’abbassamento della barriera di
potenziale:
eV
− e(Vo − V )
n p (0) = n no exp
= n po exp
k
T
k
T
B
B
Le espressioni precedenti sono note come “legge della giunzione”
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n: Polarizzazione diretta
L’iniezione di portatori minoritari da un lato e dall’altro della giunzione produce un
eccesso di portatori che diffondono finché non si ricombinano con i maggioritari e la
concentrazione diventa quella di equilibrio (pno e npo ). Con riferimento alle lacune è:
∆p n ( x ) = p n ( x ) − p no ⇒
'
'
x'
∆p n ( x ) = ∆p n (0) exp −
L p
'
L p = Dp τp
Lp è la lunghezza di diffusione delle lacune, Dp e τp rispettivamente la costante di diffusione
e il tempo medio di ricombinazione di lacune ed elettroni nel lato n
Il gradiente di concentrazione dei minoritari produce una corrente di diffusione:
J D,h
[
]
x'
dp n ( x ' )
d ∆p n ( x ' ) eD p
= −eD p
= −eD p
=
∆p n (0) exp −
'
'
L
dx
dx
Lp
p
Un discorso analogo vale per la diffusione degli elettroni
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n: Polarizzazione diretta
La corrente di diffusione tende ad annullarsi andando verso i contatti esterni e si
somma alla corrente di trasporto dei maggioritari che è invece massima in prossimità
dei contatti. La corrente totale è costante in tutta la struttura.
Andamento delle componenti
della densità di corrente totale,
supponendo trascurabile
la
ricombinazione nella regione di
svuotamento
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n: Polarizzazione diretta
La densità di corrente totale è esprimibile come somma delle correnti di diffusione di
elettroni e lacune ai due lati della regione di svuotamento, se si trascura la
ricombinazione in quest’ultima regione. Utilizzando la legge della giunzione si ha
quindi:
J D,h
eD p n i2 eV
exp
− 1 ;
=
L N
p d k BT
eD p
eD n
+
J=n
L N
p d Ln Na
2
i
J D ,e
eD n n i2 eV
exp
− 1
=
L n N a k BT
eV
eV
exp
k T − 1 = J so exp k T − 1
B
B
L’equazione precedente è detta equazione di Shockley mentre la costante Jso, che dipende dai
drogaggi Na e Nd e dal materiale attraverso le costanti e le lunghezze di diffusione, è detta
densità di corrente di saturazione inversa in quanto contribuisce alla densità corrente
che scorre nella giunzione quando è applicato un potenziale inverso, V=-Vr, maggiore
della tensione termica VT = kBT/e= kBT/q
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n: Polarizzazione diretta
La ricombinazione nella regione di svuotamento produce una variazione della corrente
esterna che serve a compensare le cariche perse per ricombinazione.
J rec
eABC eBCD
=
+
τn
τp
J rec ≈
e
Wp n M
2
τn
Wn p M
2
+
τp
e
Cioè, considerando finiti i tempi di ricombinazione, la variazione temporale di carica (corrente)
nei due lati della regione di svuotamento è pari alla carica totale diviso il tempo medio di
ricombinazione dei rispettivi portatori minoritari.
Luigi Zeni DII-SUN Optoelettronica
Giunzione p-n: Polarizzazione diretta
Le concentrazioni pM e nM possono essere facilmente determinate mediante la statistica
di Boltzmann ipotizzando che il potenziale si distribuisca in parti uguali sui due lati
della regione di svuotamento:
e(Vo − V ) p M
pM
= exp −
=
p po
2k B T N a
⇒
eV
p M = n i exp
= nM
2k B T
J rec
n
=e i
2
Wp Wn
eV
eV
+
exp
= J ro exp
τ
τ
2
k
T
2
k
T
n
p
B
B
Più in generale si dimostra che la densità corrente di una giunzione pn (diodo) è esprimibile
come:
Luigi Zeni DII-SUN Optoelettronica
eV
− 1
J = J o exp
ηk B T
η: fattore di idealità
del diodo
Giunzione p-n: Polarizzazione inversa
In condizioni di polarizzazione inversa la corrente che attraversa la giunzione è molto
piccola. La tensione applicata dall’esterno cade quasi tutta sulla regione di svuotamento,
che diventa più ampia e l’altezza della barriera di potenziale si incrementa di Vr.
J rev
eD p
eD n
=
+
L N
p d Ln Na
2 eWn i
n i +
τg
Luigi Zeni DII-SUN Optoelettronica
La densità di corrente inversa Jrev è dipendente dalla temperatura
e somma di due contributi di cui il primo è il termine Jso della
equazione di Shockley ed il secondo dipende dalla generazione
termica di coppie e-h nella regione di svuotamento, regolata dal
tempo di generazione τg
Caratteristica I-V del diodo p-n
Il fattore di idealità η vale 1 se domina la diffusione,
vale 2 se domina la ricombinazione nella regione di
svuotamento
Luigi Zeni DII-SUN Optoelettronica
Capacità della regione di svuotamento
La regione di svuotamento della giunzione p-n presenta cariche positive e negative per
una estensione spaziale W=Wn+Wp ed è simile ad un condensatore a facce piane e
parallele.
A differenza di un condensatore la carica accumulata NON dipende linearmente dalla
tensione applicata. Detta A la sezione trasversa della giunzione si ha per la carica Q:
Q = eN d Wn A ; − Q = −eN a Wp A
Variando la tensione applicata di dV, la quantità di carica varia di dQ, quindi:
C dep
dQ
=
dV
Applicando una tensione esterna V si ha, per la larghezza della zona di svuotamento:
2ε(N a + N d )(Vo − V )
W=
eN a N d
Luigi Zeni DII-SUN Optoelettronica
Capacità della regione di svuotamento
Utilizzando l’espressione della carica ai due lati della regione di svuotamento, si può
esprimere W in funzione di Q:
1
1
W = Wp + Wn = Q
+
eN a A eN d A
N N
Q = eA a d
Na + Nd
Cdep
2εe(N a N d )(Vo − V )
2ε(N a + N d )(Vo − V )
=A
eN a N d
Na + Nd
dQ
A
=
=
dV
Vo − V
εe(N a N d ) εA
=
2(N a + N d ) W
La capacità ha la stessa espressione di quella di un condensatore a facce piane e parallele ma dipende, in
maniera quadratica, dalla tensione. Cresce all’aumentare della polarizzazione diretta (V > 0) e decresce
all’aumentare della polarizzazione inversa (V < 0)
Luigi Zeni DII-SUN Optoelettronica
Capacità di diffusione
Quando la giunzione è polarizzata direttamente, si ha un eccesso di lacune sul lato n e
di elettroni sul lano p della regione di svuotamento che diffondono nelle regioni neutre.
La quantità di carica dipende dalla tensione diretta e varia con essa comportandosi
come una capacità, detta capacità di diffusione Cd, che si somma a quella della regione
di svuotamento Cdep
Dette Qp e Qn le quantità di carica dovute alle lacune ed agli elettroni iniettati, si ottiene:
∞
∞
Q p = eA ∫ ∆p n ( x )dx =eA ∫ ∆p n (0)e
0
0
∞
∞
0
0
−x Lp
(
)
(
)
dx =eALp p no e eV k BT − 1
− Q n = eA ∫ ∆n p ( x )dx =eA ∫ ∆n p (0)e − x L n dx =eALn n po e eV k BT − 1
dQ n dQ p Ae2
(L p p no + L n n po )eeV k BT
Cd =
+
=
dV
dV
k BT
Luigi Zeni DII-SUN Optoelettronica
Tempo di ricombinazione (bandgap diretto)
Quando in un semiconduttore drogato c’è un eccesso di lacune ed elettroni, la neutralità
richiede ∆np= ∆pp nel caso di drogaggio p, e ∆pn= ∆nn per drogaggio n.
Considerando, ad esempio, GaAs di tipo p, si ha:
n p = n po + ∆n p
Concentrazione istantanea dei portatori minoritari
p p = p po + ∆n p
Concentrazione istantanea dei portatori maggioritari
La velocità di ricombinazione sarà proporzionale alla concentrazione di entrambi i tipi
di portatori avendo scelto un semiconduttore a bandgap diretto e quindi con elevata
probabilità di ricombinazione diretta:
∂∆n p
∂t
= −βn p p p + G th
Gth è la velocità di generazione termica
β è il coefficiente di cattura per ricombinazione diretta
L’espressione della velocità di generazione termica si ricava considerando il sistema
all’equilibrio, per cui:
∂∆n p
Luigi Zeni DII-SUN Optoelettronica
= 0;
∂t
G th = βn po p po
n p = n po ; p p = p po ⇒
Tempo di ricombinazione (bandgap diretto)
Si ha, quindi, per l’equazione di bilancio:
∂∆n p
∂t
= −β(n p p p − n po p po ) = − U
U è detta velocità netta di ricombinazione in quanto include la generazione termica.
L’equazione precedente può essere particolarizzata ai casi di bassa ed alta iniezione
Bassa iniezione:
∆n p << p po →
∂∆n p
∂t
= −βp po ∆n p = −
∆n p
τn
τn = 1/βppo ≈ 1/βNa è detto tempo di vita medio dei portatori minoritari ed è costante
Alta iniezione:
∆n p >> p po →
∂∆n p
∂t
= −β∆p p ∆n p = −β(∆n p )
2
Non è definibile un tempo di vita medio dei portatori minoritari come una costante
Luigi Zeni DII-SUN Optoelettronica
Tempo di ricombinazione (bandgap indiretto)
In un semiconduttore a bandgap indiretto, ad esempio Silicio, i processi
di ricombinazione sono più complessi perché coinvolgono i cosiddetti
centri di ricombinazione (o livelli di trappola) ed implicano l’interazione
con fononi. Si dimostra che la velocità netta di ricombinazione, nel caso
di drogaggio n, è:
v th σ n σ p N t (p n n n − n i2 )
U=
σ n n n + n i e(E −E )/ k T + σ p p n + n i e(E −E )/ k
[
v th =
3k BT
m*e
t
i
B
]
[
i
t
BT
]
Velocità termica media degli elettroni nel cristallo
σn , σp
Sezioni di cattura della trappola rispettivamente per elettroni e lacune
Et , Nt
Livello energetico della trappola e sua concentrazione
Luigi Zeni DII-SUN Optoelettronica
Diagramma a bande della giunzione p-n
Luigi Zeni DII-SUN Optoelettronica