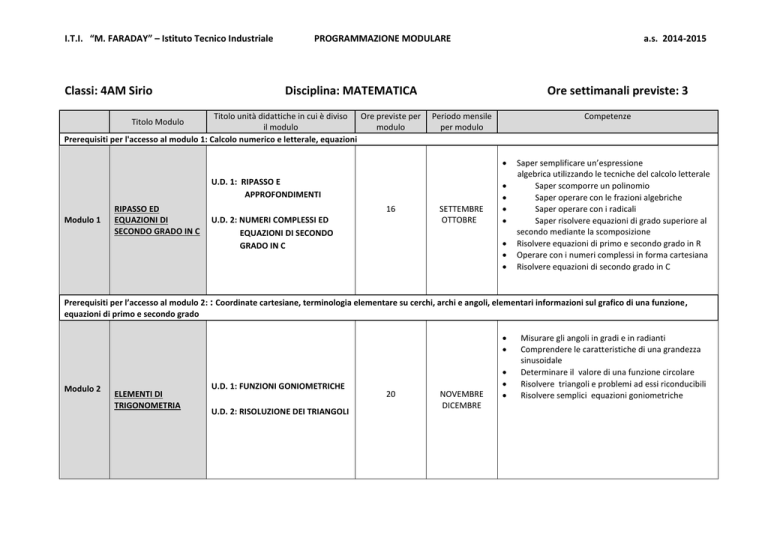
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
Classi: 4AM Sirio
PROGRAMMAZIONE MODULARE
a.s. 2014-2015
Disciplina: MATEMATICA
Titolo unità didattiche in cui è diviso Ore previste per
il modulo
modulo
Prerequisiti per l'accesso al modulo 1: Calcolo numerico e letterale, equazioni
Titolo Modulo
Ore settimanali previste: 3
Periodo mensile
per modulo
Competenze
U.D. 1: RIPASSO E
APPROFONDIMENTI
Modulo 1
RIPASSO ED
EQUAZIONI DI
SECONDO GRADO IN C
16
U.D. 2: NUMERI COMPLESSI ED
EQUAZIONI DI SECONDO
GRADO IN C
SETTEMBRE
OTTOBRE
Saper semplificare un’espressione
algebrica utilizzando le tecniche del calcolo letterale
Saper scomporre un polinomio
Saper operare con le frazioni algebriche
Saper operare con i radicali
Saper risolvere equazioni di grado superiore al
secondo mediante la scomposizione
Risolvere equazioni di primo e secondo grado in R
Operare con i numeri complessi in forma cartesiana
Risolvere equazioni di secondo grado in C
Prerequisiti per l’accesso al modulo 2: : Coordinate cartesiane, terminologia elementare su cerchi, archi e angoli, elementari informazioni sul grafico di una funzione,
equazioni di primo e secondo grado
Modulo 2
ELEMENTI DI
TRIGONOMETRIA
U.D. 1: FUNZIONI GONIOMETRICHE
U.D. 2: RISOLUZIONE DEI TRIANGOLI
20
NOVEMBRE
DICEMBRE
Misurare gli angoli in gradi e in radianti
Comprendere le caratteristiche di una grandezza
sinusoidale
Determinare il valore di una funzione circolare
Risolvere triangoli e problemi ad essi riconducibili
Risolvere semplici equazioni goniometriche
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
PROGRAMMAZIONE MODULARE
a.s. 2014-2015
Prerequisiti per l’accesso al modulo 3: Elementi di trigonometria, coordinate cartesiane, equazioni
U.D. 1 : NUMERI COMPLESSI IN
FORMA TRIGONOMETRICA
Modulo 3
10
GENNAIO
NUMERI COMPLESSI
U.D. 2: GRANDEZZE SINUSOIDALI E
NUMERI COMPLESSI
Porre in relazione coordinate cartesiane e
coordinate polari
Passare dalla rappresentazione cartesiana di un
numero complesso a quella goniometrica e
viceversa
Operare con i numeri complessi
Eseguire operazioni tra grandezze sinusoidali con il
metodo dei fasori
Prerequisiti per l'accesso al modulo 4: Equazioni e sistemi di equazioni
U.D. 1: LA FUNZIONE LINEARE E LA
RETTA
Modulo
4
PIANO CARTESIANO E
FUNZIONI NOTEVOLI
U.D. 2: LA FUNZIONE QUADRATICA
E LA PARABOLA
20
FEBBRAIO
MARZO
U.D.3: FUNZIONE ESPONENZIALE E
FUNZIONE LOGARITMICA
Calcolare distanze nel piano cartesiano
Comprendere l’andamento di grandezze lineari,
quadratiche, esponenziali e logaritmiche
Rappresentare graficamente rette e parabole e
risolvere problemi
Calcolare logaritmi
Risolvere semplici equazioni esponenziali e
logaritmiche
Prerequisiti per l'accesso al modulo 5: Semplificazione di espressioni algebriche, equazioni di 1° e 2° grado, sistemi di equazioni
U.D.1: GRAFICO PROBABILE
Modulo
5
STUDIO DI FUNZIONE
U.D.2: CALCOLO DIFFERENZIALE
21
MARZO
APRILE
MAGGIO
Risolvere disequazioni e sistemi di disequazioni
Calcolare il dominio di una funzione
Calcolare limiti e determinare il grafico probabile di
funzioni in particolare razionali fratte
Conoscere le informazioni che fornisce la derivata
di una funzione
Calcolare derivate e utilizzarle per trovare eventuali
massimi e minimi
Eseguire uno studio completo di funzione
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
PROGRAMMAZIONE MODULARE
a.s. 2014-2015
Prerequisiti per l'accesso al modulo 6: Operazioni con numeri razionali e insiemi
Modulo
6
PROBABILITA'
U.D.1: PROBABILITA’ DI EVENTI
SEMPLICI E COMPOSTI
U.D.2: CALCOLO COMBINATORIO E
PROBABILITA’
12
MAGGIO
GIUGNO
Calcolare la probabilità di un evento.
Calcolare la probabilità dell’evento unione di due
eventi.
Calcolare la probabilità dell’evento intersezione di
due eventi.
Calcolare la probabilità di eventi complessi con il
calcolo combinatorio
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
PROGRAMMAZIONE MODULARE
a.s. 2014-2015
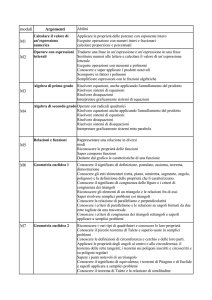
Unità didattiche del modulo N. 1: RIPASSO ED EQUAZIONI DI SECONDO GRADO IN C
Titolo U. D.
U. D. 1:
RIPASSO
Contenuti
Monomi, polinomi, prodotti
notevoli
Metodi di scomposizione dei
polinomi
Frazioni algebriche
Equazioni di primo e secondo grado
Radicali
U. D. 2:
NUMERI COMPLESSI
ED EQUAZIONI DI
SECONDO GRADO
IN C
L’unità immaginaria e i numeri
immaginari
Il campo dei numeri complessi, il
piano di Gauss e i vettori
Equazioni di secondo grado in C
Conoscenze Teoriche
Operazioni con i monomi e i
polinomi
Prodotti notevoli
Scompozione con: raccoglimento
totale e parziale, prodotti
notevoli, trinomio particolare,
Ruffini
Principi di equivalenza delle
equazioni
Formula risolutiva equazione di
secondo grado
Operazioni con frazioni algebriche
Operazioni con radicali
Rappresentazione cartesiana di un
numero complesso
Numero complesso opposto,
coniugato, inverso, modulo
Operazioni con numeri complessi
in forma cartesiana
Abilità Operative
Saper risolvere operazioni e
semplici espressioni con monomi e
polinomi
Saper risolvere equazioni di primo e
secondo grado intere e fratte
Saper scomporre un polinomio con:
raccoglimento totale e parziale,
prodotti notevoli, trinomio
particolare, Ruffini
Saper risolvere un’equazione di
grado superiore al secondo con la
scomposizione
Saper operare con le frazioni
algebriche
Saper operare con i radicali
Saper eseguire le operazioni tra
numeri complessi in forma
cartesiana
Saper rappresentare
geometricamente sul piano di Gauss
i numeri complessi con punti o
vettori
Saper determinare il modulo di un
numero complesso
Saper risolvere equazioni di
secondo grado in C
N. ore
10
6
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
PROGRAMMAZIONE MODULARE
a.s. 2014-2015
Unità didattiche del modulo N. 2: ELEMENTI DI TRIGONOMETRIA
Titolo U. D.
U. D. 1:
FUNZIONI
GONIOMETRICHE
Contenuti
Radianti
Funzioni circolari
Funzioni inverse delle funzioni
circolari
Conoscenze Teoriche
U. D. 2:
RISOLUZIONE DEI
TRIANGOLI
Risoluzione di triangoli rettangoli
Risoluzione di triangoli qualsiasi
Abilità Operative
Definizione di radiante
Definizioni di seno, coseno,
tangente e grafici delle funzioni
corrispondenti
Funzioni periodiche
Relazioni goniometriche
fondamentali
Funzioni inverse delle funzioni
circolari e loro grafici: arcoseno,
arcocoseno, arcotangente
Valori delle funzioni circolari per
angoli fondamentali
Relazione tra tangente di un
angolo e coefficiente angolare di
una retta
Cenni sulle principali formule
trigonometriche.
Relazioni tra cateti, ipotenusa e
angoli in un triangolo rettangolo.
Teorema dei seni e teorema di
Carnot
Convertire gradi sessagesimali in
radianti e viceversa
Saper determinare il valore di una
funzione circolare
geometricamente, con la
calcolatrice o conoscendo il valore
di altre funzioni circolari relative
allo stesso angolo
Saper applicare le principali formule
trigonometriche
Saper risolvere semplici equazioni
goniometriche
Saper determinare il coefficiente
angolare di una retta a partire
dall’angolo che forma con l’asse
delle X e viceversa
Saper determinare, noti alcuni
elementi di un triangolo, tutti gli
elementi rimanenti
Saper applicare i metodi per la
risoluzione dei triangoli a problemi
N. ore
10
10
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
PROGRAMMAZIONE MODULARE
a.s. 2014-2015
Unità didattiche del modulo N. 3: NUMERI COMPLESSI
Titolo U. D.
Contenuti
U. D. 1:
NUMERI COMPLESSI
IN FORMA
TRIGONOMETRICA
U. D. 2:
GRANDEZZE
SINUSOIDALI E
NUMERI COMPLESSI
Conoscenze Teoriche
Rappresentazione trigonometrica di
un numero complesso
Operazioni con i complessi in forma
trigonometrica
Grandezze sinusoidali
Metodo dei fasori
Elementi caratteristici di una
grandezza sinusoidale: ampiezza,
frequenza e fase
Fasore associato ad una grandezza
sinusoidale.
Sistema di coordinate polari.
Formule per le operazioni con i
numeri complessi
Formula di De Moivre.
Abilità Operative
Saper passare dalla
rappresentazione cartesiana a
quella trigonometrica di un
numero complesso e viceversa
Saper eseguire le operazioni tra
numeri complessi in forma
goniometrica, comprese le potenze
e le radici n-esime.
Saper utilizzare il metodo dei fasori
per eseguire la somma di
grandezze sinusoidali
isofrequenziali
N. ore
6
4
Unità didattiche del modulo N.4: PIANO CARTESIANO E FUNZIONI NOTEVOLI
Titolo U. D.
U. D.1:
LA FUNZIONE
LINEARE E LA RETTA
Contenuti
Le coordinate cartesiane
Distanza di due punti nel piano
La funzione lineare e la retta
Il parallelismo e la perpendicolarità
tra rette nel piano cartesiano
Retta per due punti
Conoscenze Teoriche
Come si introduce un sistema di
coordinate cartesiane in un piano
Formula per determinare la
distanza tra due punti
Equazione implicita ed esplicita di
una generica retta
Coefficiente angolare
Le condizioni di parallelismo e
perpendicolarità tra rette
Abilità Operative
Calcolare la lunghezza di un
segmento
Riconoscere e disegnare rette
Determinare il coefficiente
angolare di una retta
Saper calcolare il punto di
intersezione tra due rette
Saper determinare l’equazione
della retta per due punti noti
N. ore
8
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
U. D. 2:
LA FUNZIONE
QUADRATICA E LA
PARABOLA
U. D. 3:
LA FUNZIONE
ESPONENZIALE E
LOGARITMICA
La funzione quadratica
La parabola
PROGRAMMAZIONE MODULARE
Definire la parabola come luogo
geometrico.
Formule di calcolo degli elementi
che caratterizzano una parabola
Funzione esponenziale
Logaritmi
Funzione logaritmica
Definizione di funzione
esponenziale
Funzioni inverse
Definizione di logaritmo
Proprietà dei logaritmi
a.s. 2014-2015
Saper associare il modello lineare
in una situazione reale
Disegnare una parabola a partire
dalla sua equazione
Determinare vertice, asse, fuoco e
direttrice di una parabola
Saper calcolare semplici logaritmi
sia analiticamente che con la
calcolatrice
Saper applicare le proprietà dei
logaritmi
Saper risolvere semplici equazioni
esponenziali e logaritmiche
Saper associare il modello
esponenziale ad una situazione
reale
4
8
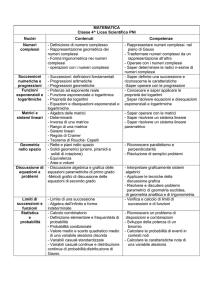
Unità didattiche del modulo N. 5: STUDIO DI FUNZIONE
Titolo U. D.
Contenuti
U. D. 1:
GRAFICO
PROBABILE
Disequazioni di primo e secondo
grado intere e fratte
Sistemi di disequazioni.
Dominio di una funzione
Limiti e asintoti di una funzione
Conoscenze Teoriche
Principi di equivalenza delle
disequazioni.
Studio del segno di fattori di
primo e secondo grado.
Definizione di dominio di
esistenza
Tipologie dei limiti
Definizione di asintoto
Abilità Operative
Saper risolvere disequazioni e
sistemi di disequazioni
Saper determinare il dominio di
esistenza di una funzione
Saper calcolare limiti soprattutto di
funzioni razionali fratte
Saper determinare gli asintoti di
una funzione razionale fratta
N. ore
11
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
U. D. 2:
CALCOLO
DIFFERENZIALE
PROGRAMMAZIONE MODULARE
Derivata di una funzione
Estremi relativi di una funzione
Definizione di derivata e suoi
significati
Derivate fondamentali e regole di
derivazione.
Definizione di massimo e minimo
relativo
C.N.e C. S. per l’esistenza di
estremi relativi.
a.s. 2014-2015
Saper calcolare derivate
Saper determinare gli intervalli di
crescenza e decrescenza di una
funzione
Saper determinare massimi e
minimi relativi
Saper interpretare un grafico
Saper determinare l’andamento
grafico di una funzione
10
Unità didattiche del modulo N. 6: PROBABILITA’
Titolo U. D.
U. D. 1:
PROBABILITA’ DI
EVENTI SEMPLICI E
COMPOSTI
Contenuti
Gli eventi e la probabilità
La probabilità della somma logica di
eventi
La probabilità del prodotto logico di
eventi
Probabilità condizionata
Conoscenze Teoriche
Conoscere il significato di:
- evento e di probabilità
- evento certo, evento
impossibile, evento contrario
- eventi compatibili e incompatibili
- eventi dipendenti e indipendenti
Formula calcolo probabilità
somma logica di eventi
Formula calcolo probabilità
prodotto logico di eventi
Abilità Operative
Riconoscere eventi certi,
impossibili, aleatori e calcolarne la
probabilità.
Calcolare la probabilità dell’evento
contrario .
Riconoscere eventi compatibili,
dipendenti e non.
Calcolare la probabilità della
somma e del prodotto logico
N. ore
6
I.T.I. “M. FARADAY” – Istituto Tecnico Industriale
U. D. 2:
CALCOLO
COMBINATORIO E
PROBABILITA’
PROGRAMMAZIONE MODULARE
Il calcolo combinatorio: disposizioni,
permutazioni, combinazioni e
fattoriale e binomiale
Calcolo combinatorio e probabilità
di eventi complessi
Conoscere tutti i tipi di
raggruppamenti
Conoscere il fattoriale e il
coefficiente binomiale
a.s. 2014-2015
Calcolare quanti gruppi si possono
formare con n oggetti presi k alla
volta sapendo abbinare ai casi reali
il giusto modello matematico:
disposizioni semplici e con
ripetizione, permutazioni,
combinazioni semplici
Calcolare la probabilità di eventi
mediante il calcolo combinatorio
6