Ogni misura è composta di almeno tre dati:
un numero, un'unità di misura, un'incertezza.
Misure ripetute forniscono dati numerici distribuiti attorno ad un
valore centrale indicabile con un indice (indice di localizzazione
o di posizione). A seconda dei casi si potrà adottare l'uno o l'altro
indice in base all'esperienza.
Indici di localizzazione
Media aritmetica: x = Σixi/N dove xi sono i risultati delle N misure.
"Scarto dalla media" o scarto: (xi - x). La media aritmetica
costituisce il legame (vincolo) tra la somma dei dati (Σ
Σ xi) ed il loro
numero (N), e gode delle seguenti proprietà:
1) Σ (xi - x) = 0, per cui gli scarti indipendenti sono (N-1).
2) Σ (xi - x)2= minimo (metodo dei minimi quadrati).
Frequenza dati
La media si applica direttamente alla curva normale dell’errore,
curva di Gauss,
x≡µ
Frequenza dati
Altri indici di posizione si applicano ad altri tipi di
distribuzione, come questa di frequenze unimodali e
modestamente asimmetrica:
x≡µ
b) MODA: valore cui corrisponde il massimo di frequenza.
c) MEDIANA: valore che divide in due il campo di misura, quando
i dati replicati sono ordinati in ordine crescente o decrescente,
con metà dati a destra e metà a sinistra (media dei valori di
mezzo se n è pari).
Questi indici di posizione sono significativi in alcuni casi
particolari, ma sono insensibili a quanto avviene ai margini.
In una distribuzione di frequenze unimodale e moderatamente
asimmetrica, gli indici di posizione sono legati fra loro secondo la
relazione empirica:
[(MEDIA – MODA) = 3 (MEDIA - MEDIANA)]
Moda
Mediana
Media
Un'estensione del concetto di mediana (valore che divide
l'insieme dei dati in due parti uguali) è quello che riguarda i valori
che dividono l'insieme in quattro parti uguali. Tali valori
vengono chiamati "quartili".
0
25
I quartile
50
II quartile
75
III quartile
100
IV quartile
Allo stesso modo, vengono definiti "decili" e "percentili" i valori
che dividono l'insieme dei dati rispettivamente in 10 e 100 parti
uguali.
d) MEDIA TRONCATA: si calcola come media aritmetica della
porzione centrale dei dati ; vengono scartate (di solito
simmetricamente) le code della distribuzione.
e) MEDIA GEOMETRICA: rappresenta il prodotto di N numeri.
Media geometrica = N√πi xi
i=1 → N
Il simbolo π indica il prodotto di tutti i valori.
In relazione alla diversa sensibilità ai dati aberranti, la media ne
è influenzata, la mediana non è influenzata dalla loro presenza, la
media troncata rappresenta un compromesso tra le prime due, in
quanto si basa su un numero consistente di dati ma non usa gli
estremi del campione, tra i quali si possono trovare i valori
aberranti.
Indici di dispersione
a) CAMPO DI VARIAZIONE: Il modo più semplice per indicare la
variabilità di un insieme di dati, è di esprimerlo come differenza tra
il più grande (valore massimo) ed il più piccolo (valore minimo)
dei dati sperimentali o misure.
b) DEVIAZIONE MEDIA (Mean Deviation): MD = [∑
∑ xi – x ]/N
Viene definita anche «scostamento semplice medio assoluto dalla
media aritmetica»
∑(xi – x)2
c) DEVIAZIONE STANDARD:
√
(N-1)
La deviazione standard, chiamata anche scarto quadratico medio,
viene indicata con s.
s è cioè la radice quadrata dei quadrati degli scarti dalla media
aritmetica divisi per il numero di gradi di libertà.
d) VARIANZA: s2 = [∑
∑ (xi - x)2] / (N-1)
La varianza di un insieme di dati è definita come il quadrato della
deviazione standard.
Quando il numero di dati sperimentali disponibili è molto
elevato (al limite tende ad infinito) la deviazione standard è
definita dalla relazione: σ = √ [∑
∑ (xi – x)2] / N dove xi è la misura
iesima, x è la media e N il numero di prove.
Nel caso più frequente, in cui i dati sperimentali sono limitati, la
deviazione standard viene stimata attraverso la grandezza s
definita dalla relazione: s = √ [∑
∑ (xi – x)2] / (N – 1) dove N-1
rappresenta i gradi di libertà.
Si utilizza s, al posto di σ per evidenziare il fatto che, avendo a
disposizione una serie limitata di dati, non si ha la pretesa di
calcolare la deviazione standard, ma solo di darne una
valutazione che risulterà tanto più attendibile quanto maggiore è
il numero di prove effettuate.
Proprietà della deviazione standard o dello scarto
quadratico medio
Se la variabile x ha distribuzione normale con media x e varianza
s2, allora:
a) Il 68,27% dei casi è compreso tra x – s e x + s (cioè una
deviazione standard da ogni parte della media).
b) Il 95,45% dei casi è compreso tra x – 2s e x + 2s (cioè due
deviazioni standard da ogni parte della media).
c) Il 99,73% dei casi è compreso tra x – 3s e x + 3s (cioè tre
deviazioni standard da ogni parte della media).
Quando N tende ad infinito, il valore medio delle misure
sperimentali (in assenza di errori sistematici) tende al valore
vero, convenzionalmente indicato con µ, mentre la deviazione
standard stimata s (o campionaria) tende alla deviazione
standard della popolazione σ.
Il valore di s (deviazione standard campionaria) indica la
imprecisione di una misura ed è legata agli errori casuali.
Quindi l’imprecisione, di solito, viene espressa come deviazione
standard (s) e descrive l’accordo tra due o più misure replicate,
cioè la vicinanza reciproca delle misure all’interno di un insieme
di misurazioni e risulta correlata agli errori casuali.
Più utile può essere l’espressione della imprecisione (come
ripetibilità o riproducibilità) in termini di coefficiente di
variazione o deviazione standard relativa percentuale
(RSD%), cioè di imprecisione percentuale : CV = RSD % =
[s / x] x 100
È chiaro che ad un piccolo CV corrisponde poca dispersione dei
dati attorno ad un valore medio e quindi un’elevata precisione ed
una bassa imprecisione.
Il Laboratorio può stimare la imprecisione del proprio metodo
effettuando misure replicate dello stesso materiale di controllo
nella stessa serie analitica (ripetibilità, imprecisione entrosaggio), oppure in serie analitiche differenti (riproducibilità,
imprecisione tra-saggi).
È evidente che la ripetibilità risulterà migliore della
riproducibilità; infatti, nella replica dello stesso campione in serie
analitiche differenti, concorreranno ad aumentare la variabilità
anche cause di errore (differenze nelle condizioni sperimentali del
saggio, differenze nei reattivi) che non sono presenti quando le
misure vengono replicate all’interno della stessa serie analitica.
Per lo stesso motivo la riproducibilità calcolata da replicati
eseguiti in un periodo molto lungo potrà risultare più elevata
rispetto a quella stimata da replicati eseguiti in un intervallo di
tempo relativamente più breve.
Dispersione o Range: è un altro termine che spesso viene
utilizzato per descrivere la precisione di un insieme di risultati
replicati. Esso è la differenza tra il valore più grande e quello più
piccolo dell’insieme.
Livelli di fiducia
Il valore esatto della media per una popolazione di dati non può
mai essere determinato con assoluta precisione perché
richiederebbe un infinito numero di misure.
La teoria statistica ci permette comunque di fissare dei limiti
attorno ad una media sperimentale x nei quali il valore vero µ si
trova con una certa probabilità.
Questi limiti sono denominati limiti di fiducia e l’intervallo da essi
definito è noto come intervallo di fiducia.
L’estensione dell’intervallo di fiducia, che deriva dalla deviazione
standard del campione, dipende dall’accuratezza di s.
I limiti di fiducia definiscono quindi un intervallo attorno ad x che
con una certa probabilità contiene µ.
L’intervallo di fiducia è, a sua volta, definito dai limiti di fiducia.
Il livello di fiducia fissa i limiti entro cui deve trovarsi il valore vero.
L’espressione generale per i limiti di fiducia (LF) di una singola
misura è data dall’equazione:
LF per µ = x ± zσ
Per la media di N misure si utilizza l’errore standard della media
σ/√
√N al posto di σ, per cui LF per µ = x ± zσ/√N
Quando non si conosce σ, ma si dispone di s, che essendo
ottenuto da un piccolo insieme di dati, può essere piuttosto incerto
e quindi affetto da notevole variabilità.
Come conseguenza, non disponendo di una buona stima di σ, i
limiti di fiducia saranno necessariamente più ampi.
Per tenere in considerazione la variabilità di s, si utilizza
l’importante parametro statistico t (t di Student), definito
dall’equazione:
x-µ
t =
s
Il valore di t dipenderà dal livello di fiducia desiderato ed anche
dal numero di gradi di libertà utilizzati nel calcolo di s.
I limiti di fiducia per la media x di N misure replicate possono
essere derivati da t attraverso l’equazione:
LF per µ = x ±
ts
√N
Il Metodo dei Minimi Quadrati per la
realizzazione di Curve di Calibrazione
La maggior parte dei metodi analitici è basata su
curva
di
calibrazione
ricavata
una
sperimentalmente, in cui viene riportata una
quantità
misurata
(y)
in
funzione
della
concentrazione nota (x) di una serie di standard.
y
x
Esiste una tecnica statistica, chiamata Analisi di
Regressione,
Regressione che consente di ottenere tale retta
in maniera obiettiva, e di specificare le incertezze
associate al suo utilizzo.
Normalmente, a causa degli errori indeterminati
associati al processo di misurazione, non tutti i
punti si trovano esattamente sulla retta.
Di conseguenza, è necessario cercare di
derivare la retta “migliore”
migliore” che interpoli i punti.
Consideriamo la procedura di regressione più
più
semplice, il metodo dei minimi quadrati.
quadrati.
Per applicare questo metodo deve esistere una
relazione lineare tra la variabile misurata (y) e la
concentrazione dell’analita (x).
Questa relazione è espressa come:
y = a + bx
a intercetta (sull’asse delle y)
b coefficiente di regressione, pendenza della retta
La deviazione verticale di un punto dalla retta è
chiamato residuo.
Assorbanza
5
4,5
4
3,5
3
2,5
2
1,5
1
0,5
0
Residuo = yi – (bxi + a)
0
0,5
1
1,5
2
2,5
Concentrazione
La linea costruita con il metodo dei minimi quadrati è tale da
minimizzare la somma dei quadrati dei residui corrispondenti a
tutti i punti.
Si può dimostrare che per l’equazione di questa retta, che è del
tipo y = a + bx, il coefficiente angolare b (coefficiente di
regressione) è dato dalla relazione.
Σ (xi – x) (yi – y)
b=
Σ (xi – x)2
Dove xi sono tuti i valori della variabile indipendente x ed yi quelli
della variabile dipendente y.
L’intercetta a si ottiene poi dall’equazione: a = y - bx
Per stabilire fino a che punto l’equazione di regressione calcolata
con il metodo dei minimi quadrati può essere usata al fine di
trovare un valore di x conoscendo quello di y, si calcola un
particolare parametro, chiamato coefficiente di determinazione.
[ Σxy – (Σ
Σx)(Σ
Σy)/n ]2
R2 =
[ Σx2 – (Σ
Σx)2/n] [ Σy2 – (Σ
Σy)2/n]
R2 può assumere valori compresi tra 0 ed 1. Se R2 = 1 esiste una
perfetta relazione lineare fra x ed y, per cui ad un determinato
valore di x corrisponde uno ed un solo valore di y.
La radice quadrata del coefficiente di
determinazione è il coefficiente di correlazione:
r = √R2
r può assumere valori compresi tra -1 ed +1
Un coefficiente di correlazione > 0,99 viene
considerato in indicatore di linearità
β-CAROTENE negli oli di semi (λ = 464nm)
Abs
ppm
STD 5 3,4810
20,00
STD 4 1,7517
10,00
STD 3 0,3747
2,00 a =
0,01751
STD 2 0,1134
0,50 b = 0,17327
STD 1 0,0412
0,25 r =
0,99997
4,0000
3,5000
3,0000
Abs
2,5000
y = 0,0175 + 0,1733x
2,0000
1,5000
R2 = 0,9999
1,0000
0,5000
0,0000
0,0
5,0
10,0
15,0
ppm
20,0
25,0
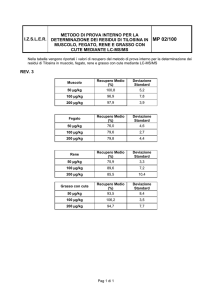
β-CAROTENE negli oli di semi (λ = 464nm)
x = (y - a)/b
conc (ppm) = (Abs - 0,0175)/0,1733
Abs
ppm
girasole 0,0304
0,1
mais
0,1771
0,9
zucca
0,9713
5,5
LA SENSIBILITÀ
La sensibilità di un metodo indica quanto esso sia
sensibile alle variazioni di concentrazione di un
analita. Può essere individuata attraverso la
pendenza (b) della retta.