Segnali trattati sino ad ora: continui, durata infinita, ..
Su essi sono stati sviluppati strumenti per analizzare output di
circuiti e caratteristiche del segnale:
Risposta all’impulso, prodotto di convoluzione, trasformata di
Fourier, autocorrelazione....
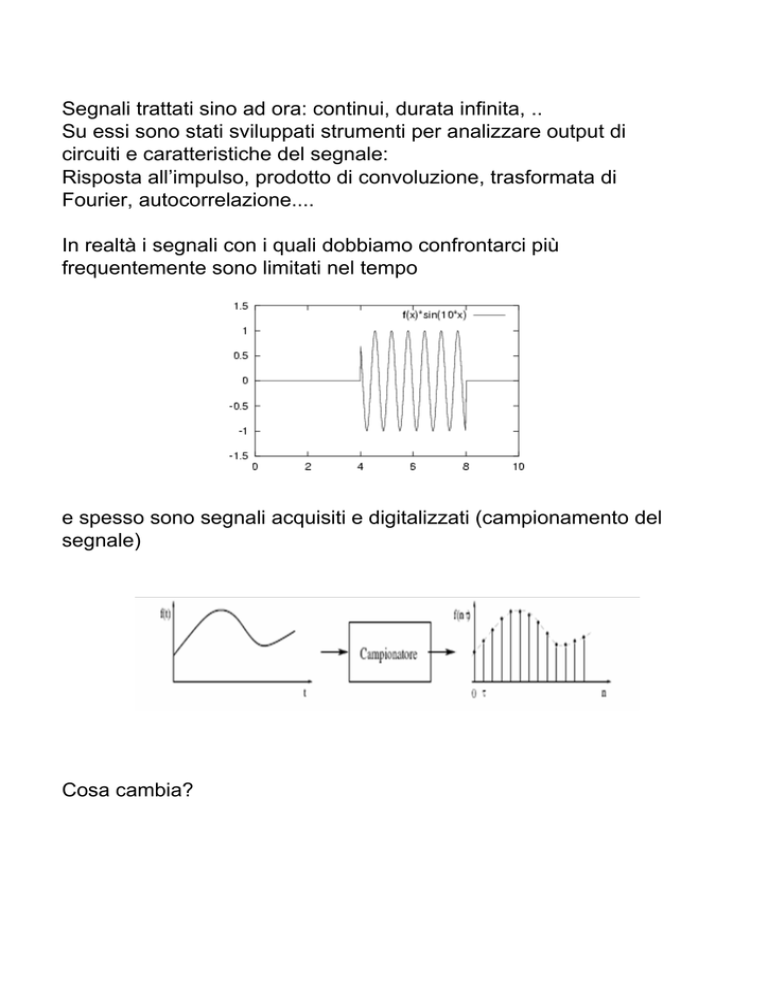
In realtà i segnali con i quali dobbiamo confrontarci più
frequentemente sono limitati nel tempo
e spesso sono segnali acquisiti e digitalizzati (campionamento del
segnale)
Cosa cambia?
Si possono trattare i segnali discreti e limitati nel tempo come
moltiplicazione di segnali di durata infinita per “finestre” temporali e
treni di impulsi
Segnale di durata infinita
Finestra rettangolare
Treno di impulsi
Segnale campionato
Il prodotto di segnali nel dominio del tempo diventa un prodotto di
convoluzione nel dominio della frequenza
Campionamento dei segnali
Le variazioni del segnale proveniente dal mondo fisico sono
trasformate in segnali elettrici da opportuni trasduttori.
Tali segnali hanno variazioni continue nel tempo, ma le misurazioni
vengono effettuate solo in istanti precisi.
Un fenomeno continuo viene quindi rappresentato come una
sequenza discreta nel tempo.
Campionare un segnale a tempo continuo significa rilevare le
ampiezze del segnale su un insieme discreto di tempi.
Esempio: dato un segnale f(t) (figura sopra) definito un intervallo di
campionamento τ, campionare il segnale significa acquisirne il
valore ai tempi nτ con − ∞ < n < ∞
Il segnale campionato può essere interpretato come il segnale a
tempo discreto f(nτ)
Problema:
Quando un segnale campionato f(nt) contiene le stesse informazioni
di f(t)?
Ovvero:
Quando possiamo ricostruire f(t) da un segnale campionato f(nt) ?
Segnali a banda limitata
La banda occupata da un segnale è la regione di frequenze al di
fuori della quale non vi sono componenti energetiche; la sua misura
in Hz è indicata come larghezza di banda.
Per segnali reali l'occupazione di banda è espressa in termini del
solo contenuto a frequenze positive; dato che in tal caso lo spettro di
potenza è una funzione pari di f, la banda totale è doppia.
Un segnale f(t) è detto a banda limitata con langhezza di banda W
se
per
ω >W
F (ω ) = 0
NOTA:
Se un segnale è strettamente limitato in banda, deve avere durata
infinita, e viceversa. E' pratica comune, invece, parlare di limitazione
in banda anche per segnali di durata finita. Nel fare questo, si
considera un X(f) pari a zero per le frequenze f tali che X (f ) < ε
ovvero considerare anziché X (f) a banda illimitata, una sua finestra
in frequenza XW (f)= X(f)W(f) a banda limitata.
Teorema del campionamento (Teorema di Shannon 1949)
Dato un segnale x(t) a banda limitata con larghezza di banda W, può
essere univocamente ricostruito dai suoi campioni x(nτ) presi ad
intervalli di campionamento
TS ≤
1
2W
ovvero ad una frequenza di campionamento Fs ≥ 2W
2W è detta anche frequenza di Nyquist
ovvero
Un segnale con spettro nullo a frequenze maggiori di W,
è univocamente definito a partire dai valori che assume
agli istanti t =
, con n intero
Segnale campionato = segnale originario x treno impulsi
Trasformata di un treno di impulsi
L'approccio che conviene seguire è di pensare a πT (t ) come ad un
segnale periodico, e svilupparlo in serie di Fourier. I coefficienti si
calcolano allora come:
in quanto, tra tutti gli impulsi della sommatoria, ne resta solo uno,
quello centrato in zero, dato che gli altri sono tutti esterni ai limiti di
integrazione; pertanto, tutti i coefficienti risultano avere lo stesso
valore, pari ad 1/T , e possiamo dunque scrivere
Prodotto nello spazio reale = convoluzione nello spazio delle frequenze
La convoluzione ci restituisce una serie di immagini di X(f) traslate di
± n/T con T periodo di campionamento
Le immagini non saranno sovrapposte solo se T ≤ 1/2W
X
Passa-basso
Con un filtro passa-basso ritrovo lo spettro del segnale originario
Aliasing
Fenomeno che avviene quando non si rispettano i criteri del
teorema di campionamento
Se T>1/2W le copie degli spettri della funzione originaria non sono
più distinti tra loro
Il filtro passa basso in uscita non è più in grado di restituire lo
spettro originario. Alla sua uscita è presente y (t) ≠ x (t) , che si
differenzia da x (t) in particolar modo per i contenuti energetici
nella regione delle frequenze più elevate.
In un segnale audio, ad esempio, ci si accorge che c'è aliasing
quando è udibile una distorsione (rumore) congiuntamente ai
passaggi con maggior contenuto di alte frequenze.
Esempio: onda sinusoidale con f
crescente campionata sempre
alla stessa frequenza
ωS =
ω0
6
ωS =
2ω 0
6
ωS =
4ω 0
6
ωS =
5ω 0
6
Il fenomeno dell'aliasing può insorgere, oltre che nel caso in cui si
commetta il banale errore di adottare Tc > 1/2W, anche a causa di
una imperfetta limitazione in banda di x (t) (che viene in genere
filtrato proprio per accertarsi che sia X(f)~ 0 con f > W).
Altri problemi possono essere causati dal filtro di restituzione H(f),
che difficilmente si riesce a realizzare ideale. Questo può
presentare infatti una regione di transizione tra banda passante e
banda soppressa di larghezza non nulla. In questo caso occorre
sovracampionare con periodo
Tc =
1
2W '
<
1
2W
in modo che le repliche spettrali siano più distanziate tra loro, e
quindi il filtro di ricostruzione possa isolare la replica centrale.
In opportune condizioni un segnale discreto (campionato) può
contenere tutte le informazioni del segnale originario e quest’ultimo
può essere ricavato utilizzando un filtro passa-basso.
Su un segnale discreto possono essere fatte molte operazioni:
• può essere convertito in un segnale digitale e memorizzato
• può essere manipolato da algoritmi software
• .....
Quali degli strumenti sviluppati per segnali continui possono essere
utilizzati per segnali discreti e nel caso che modifiche bisogna
apportare?
Risposta all’impulso discreto e convoluzione
Dati xn sequenza in input e yn sequenza di output e assunto che
il sistema discreto sia LTI si può caratterizzare tramite la risposta
all’impulso come nel caso continuo.
Sistema discreto LTI:
Dati x1n e x2n (due input separati) e y1n e y2n (rispettive uscite) allora
se xn= x1n + x2n → yn= y1n + y2n (linearità)
se xn-m segnale di ingresso ritardato → il sistema genera yn-m (uscita
ritardata)
Dato xn=δn,0 (delta di Kronecker) e la risposta del sistema hn allora
ogni segnale generico in ingresso darà in uscita:
yn =
∞
x j hn
∑
j
= −∞
−j
Analogo discreto dell’integrale
di convoluzione
o sostituendo m=n-j
yn =
∞
x n m hm
∑
m
= −∞
−
Nel caso di sistemi continui abbiamo trovato che est è autofunzione
∞
per il sistema con autovalore
H (s ) = ∫ h (τ )e −sτ d τ
−∞
Per un sistema discreto est → zn con -∞< n <∞
Se xn=zn allora
yn =
∞
∑z
m = −∞
con
X (z ) =
∞
n −m
hm = z
H (z ) =
−m
z
∑ xm
m = −∞
n
∞
−m
n
z
h
=
z
H (z )
∑ m
m = −∞
∞
−m
z
∑ hm
m = −∞
è definita trasformata z
Trasformata discreta di Fourier (DFT) e Fast Fourier Transform (FFT)
Il calcolo della trasformata discreta di Fourier richiede di moltiplicare un vettore a
N componenti [f(0),....f(N-1)] per una matrice NxN la cui componente alla riga n e
colonna k è
i 2πnk
−
e
N
Tale calcolo richiede un numero di operazioni di somma e prodotto dell’ordine di
N2 → richiede troppo tempo
Es. se per una operazione si impiega un microsecondo con 1000 campioni si
impiegherà 1 secondo a calcolare la DFT.
Esistono alcuni algoritmi che semplificano i conti riducendo a N log(N) il numero di
operazioni (nel caso dell’esempio sopra si impiega un tempo 100 volte minore)
FAST FOURIER TRASFORM
Quindi posso calcolare la trasformata di un vettore a N componenti sommando
le trasformate di 2 vettori a N/2 componenti
Utilizzabile quando il numero di elementi del vettore è una potenza di 2










