Funzioni Goniometriche
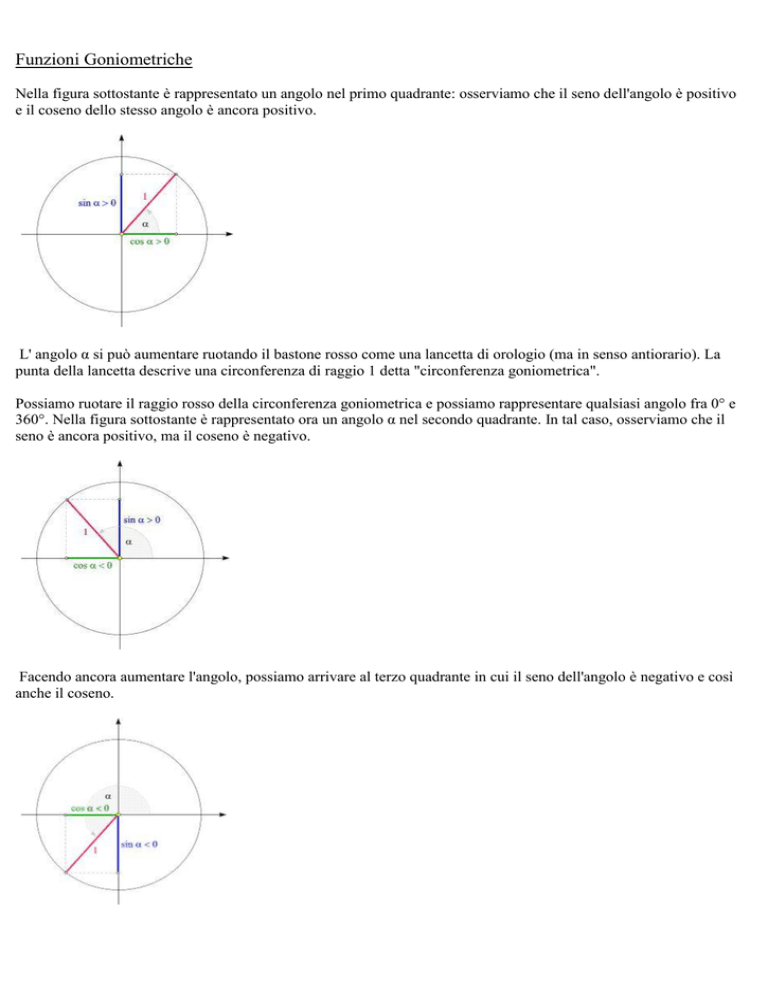
Nella figura sottostante è rappresentato un angolo nel primo quadrante: osserviamo che il seno dell'angolo è positivo
e il coseno dello stesso angolo è ancora positivo.
L' angolo α si può aumentare ruotando il bastone rosso come una lancetta di orologio (ma in senso antiorario). La
punta della lancetta descrive una circonferenza di raggio 1 detta "circonferenza goniometrica".
Possiamo ruotare il raggio rosso della circonferenza goniometrica e possiamo rappresentare qualsiasi angolo fra 0° e
360°. Nella figura sottostante è rappresentato ora un angolo α nel secondo quadrante. In tal caso, osserviamo che il
seno è ancora positivo, ma il coseno è negativo.
Facendo ancora aumentare l'angolo, possiamo arrivare al terzo quadrante in cui il seno dell'angolo è negativo e così
anche il coseno.
Infine, possiamo considerare un angolo nel quarto quadrante, in cui il seno è negativo, ma il coseno è positivo.
In ogni caso, quindi, riportando le proiezioni del raggio sugli assi cartesiani , possiamo definire il seno e il coseno
per un angolo qualsiasi, adottando la seguente convenzione: un segmento orientato verso sinistra oppure verso il
basso rispetto all'origine è considerato negativo.
Con l'ausilio della circonferenza goniometrica possiamo dimostrare una serie di proprietà basilari delle funzioni
trigonometriche. La circonferenza goniometrica è uno strumento importante per la comprensione di seno e coseno.
Una delle proprietà che si ricavano dalla circonferenza goniometrica riguarda il codominio di seno e coseno: I valori
di queste funzioni non possono mai essere minori di 1 o maggiori di 1. Questo si deduce immediatamente dal fatto
che le proiezioni del raggio (di lunghezza 1) sugli assi non possono essere più lunghe del raggio stesso.
Le funzioni seno e coseno possiedono varie proprietà. Vediamone alcune.
Consideriamo un triangolo rettangolo, la cui ipotenusa abbia lunghezza 1. Il teorema di Pitagora dice che in un
triangolo rettangolo la somma dei quadrati delle lunghezze dei due cateti coincide con il quadrato della lunghezza
dell'ipotenusa. Applicandolo al triangolo sottostante, otteniamo per qualsiasi angolo α l'identità
Questa formula fornisce una semplice relazione fra seno e coseno. Se ad esempio, per un certo angolo α,
conosciamo sin α, possiamo dedurre
dove il segno dipende dal quadrante in cui si trova il raggio che rappresenta l'angolo α nella circonferenza
goniometrica (nel primo e nel quarto quadrante +, altrimenti -).
La circonferenza goniometrica ci mostra che seno e coseno sono funzioni periodiche. Quando a un angolo α
sommiamo 360°, il raggio ritorna nella stessa posizione di α. Quindi abbiamo
Oltre a seno e coseno si usano anche altre funzioni da loro derivate. In particolare i quozienti di seno e coseno hanno
un nome proprio: tangente e cotangente. Ecco la definizione:
A differenza del seno e del coseno, per certi angoli la tangente non è definita. Si provi ad esempio a calcolare
tan(90°). Dalle definizioni date sopra infatti deduciamo:
• se cos α = 0 (cosa che si verifica quando α = 90° oppure 270°, dove l'ultimo caso è equivalente a -90), il
denominatore nella definizione di tangente diventa zero. In questi casi dunque tan α non è definita.
• se sin α = 0 (cosa che si verifica quando α = 0° oppure ±180°), il denominatore nella definizione di cotangente
diventa zero. In questo caso tang α = 0.
Anche la tangente può essere interpretata come rapporto fra i lati in un triangolo rettangolo.
Per le definizioni date prima, si deduce che in un triangolo rettangolo:
Come esempio applicativo consideriamo il seguente problema geodetico. La vetta di un monte alto 1.24 km viene
osservata sotto un angolo di 19.5°. A che distanza si trova l'osservatore dalla proiezione sul piano della vetta del
monte?
Soluzione: Consideriamo il triangolo rettangolo nello schizzo.
Usiamo la relazione trovata in precedenza:
Quindi d = 1.24 km/tan(19.5°). Usando una calcolatrice otteniamo tan(19.5°) = 0.3541, dunque d = 1.24 km/0.3541
= 3.502 km approssimativamente.
La scomposizione dei vettori
Ogni vettore a si può scomporre in modo unico nelle sue due proiezioni ax e ay lungo due rette fissate. Fissiamo nel
piano un sistema di riferimento cartesiano ortogonale di origine O e scegliamo un vettore a.
Si possono determinare le proiezioni del vettore a lungo i due assi come nella figura sottostante:
Il vettore ax è la proiezione di a lungo l'asse x e analogamente il vettore ay proiezione di a lungo l'asse y.
Applicando la trigonometria al triangolo che si ottiene:
si ottengono le componenti del vettore a:
ax = a cos θ
ay = a sen θ
Facciamo ora un esempio che capirne l’utilità.
Un aeroplano decolla da un aeroporto e viene successivamente avvistato ad una distanza di 215 km dall’aeroporto e
in una direzione che fa un angolo di 22° Est rispetto al Nord geografico.
Quali sono le componenti della spostamento?
Facciamo un disegno per evidenziare la situazione espressa dal problema:
Proviamo ora a fare i calcoli:
dx = d cos θ = (215 km) (cos 68°) = 81 km
dy = d sen θ = (215 km) (sen 68°) = 109 km
Made with Namu6












