I TEOREMI
DI EUCLIDE
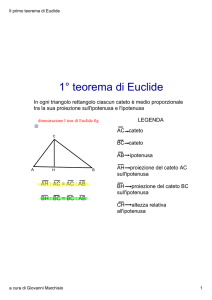
1° Teorema di Euclide
Dato il triangolo rettangolo ABC:
consideriamo i triangoli ABC e ABH simili
I due triangoli sono simili perché se consideriamo gli angoli:
- l'angolo A è comune a tutti e due (è quindi lo stesso);
- i due triangoli hanno entrambi un altro angolo che è retto (l'angolo in B per il primo triangolo e
l'angolo in H per il secondo triangolo;
- visto che la somma degli angoli interni di un triangolo misura 180°, il terzo angolo dovrà per forza
essere congruente (l'angolo in C del primo triangolo e l'angolo in B del secondo)
Stabilito che i due triangoli rettangoli sono simili, vediamo adesso quali sono i lati
corrispondenti:
ipotenusa
cateto minore
cateto maggiore
triangolo ABC
AC
AB
BC
triangolo ABH
AB
AH
BH
ALLORA POSSIAMO SCRIVERE LA PROPORZIONE:
in parole:
in un triangolo rettangolo un cateto (AB) è
AC : AB = AB : AH
medio proporzionale tra l'ipotenusa (AC) e
la proiezione del cateto stesso
sull'ipotenusa (AH)
Per il triangolo ABC allora, possiamo scrivere le proporzioni:
AC : AB = AB : AH
e
AC : BC = BC : HC
(*)
noti due dei tre elementi, le proporzioni possono essere utilizzate per calcolare:
2
AB
- l'ipotenusa AC =
AH
- un cateto AB = AC x AH
2
AC = BC
HC
BC = AC x HC
- la proiezione del cateto sull'ipotenusa AH = AB
AC
(*) si ricava dal confronto tra i triangoli simili ABC e BCH
2
2
HC = BC
AC
Calcola il perimetro di un triangolo rettangolo
in cui il cateto minore è lungo 6 cm e la sua
proiezione
3,6 cm.
DATI sull'ipotenusa
INCOGNITA
AB = 6 cm
AH = 3,6 cm
6c
m
Problema
2p = ?
3,6 cm
RISOLUZIONE
per calcolare il perimetro, devo prima calcolare i lati mancanti:
AB
62 362
(applicando il 1° teor. di AC =
=
=
= 10 cm
AH
3,6
3,6
Euclide)
(applicando il teor. di
Pitagora)
2
2
2
2
BC = AC - AB = 10 - 6 = 100 - 36 = 64 = 8 cm
2p = AC + AB + BC = 10 + 6 + 8 = 24 cm
INTERPRETAZIONE GEOMETRICA DEL 1° TEOREMA DI EUCLIDE
"In ogni triangolo rettangolo il
quadrato costruito sul cateto è
equivalente al rettangolo che ha
per dimensioni la sua
proiezione sull'ipotenusa e
l'ipotenusa stessa"
Infatti da: AC : AB = AB : AH
2
AB
= AH x AC*
deriva:
area del quadrato
costruito sul cateto
area del rettangolo
AHJL *poiché AJ = AC
e da: AC : BC = BC : HC
deriva: BC 2= HC x AC*
area del quadrato
costruito sul cateto
area del rettangolo
HCKL *poiché CK = AC
2° Teorema di Euclide
* *
Dato il triangolo rettangolo ABC:
*
*
consideriamo i triangoli ABH e BHC simili
*
*
*
*
I due triangoli sono simili perché se consideriamo gli angoli:
- l'angolo in H è retto in entrambi i triangoli;
- gli angoli ABH e BCH sono congruenti poiché:
[
HBC + ABH = 90°
[ BAH + ABH = 90°
- gli angoli HBC e BAH sono congruenti poiché:
ABH + HBC = 90°
BCH + HBC = 90°
Stabilito che i due triangoli rettangoli sono simili, vediamo adesso quali sono i lati
corrispondenti:
ipotenusa
cateto minore
cateto maggiore
triangolo ABH
AB
AH
BH
triangolo BCH
BC
BH
HC
ALLORA POSSIAMO SCRIVERE LA PROPORZIONE:
in parole:
in un triangolo rettangolo l'altezza relativa
AH : BH = BH : HC
all'ipotenusa (BH) è medio proporzionale
tra le proiezioni dei cateti sull'ipotenusa
(AH e HC)
Per il 2° teorema di Euclide
allora, possiamo scrivere:
AH : BH = BH : HC
e dalla proporzione possiamo ricavare:
- l'altezza del triangolo:
BH = AH x HC
BH
- la proiezione del cateto minore sull'ipotenusa: AH = HC
2
- la proiezione del cateto maggiore sull'ipotenusa: HC = BH
AH
2
problema
L'altezza relativa all'ipotenusa di un triangolo
rettangolo misura 7,2 cm e la proiezione del cateto
minore sull'ipotenusa 5,4 cm. Calcola il perimetro
del triangolo
rettangolo
DATI
INCOGNITA
BH = 7,2 cm
AH = 5,4 cm
2p = ?
7,2 cm
5,4 cm
RISOLUZIONE
calcolo la proiezione del cateto maggiore sull'ipotenusa (HC) utilizzando il 2° teor. di Euclide:
(AH : BH = BH : HC)
2
2
HC =
BH 7,2 51,84
=
=
= 9,6 cm
AH 5,4 5,4
adesso posso trovare il valore dell'ipotenusa AC:
AC = AH + HC = 5,4 + 9,6 = 15 cm
possiamo calcolare i due cateti del triangolo ABC applicando invece il 1° teor. di Euclide:
(AC : AB = AB : AH)
AB = AC x AH = 15 x 5,4 = 81 = 9 cm
(AC : BC = BC : HC)
[
(*)
BC = AC x HC = 15 x 9,6 = 144 = 12 cm
e infine il perimetro:
2p = AC + AB + BC = 15 + 9 + 12 = 36 cm
(*) possono essere calcolati anche applicando il teor di Pitagora ai triangoli rettangoli ABH e BCH
INTERPRETAZIONE GEOMETRICA DEL 2° TEOREMA DI EUCLIDE
"In ogni triangolo rettangolo il
quadrato costruito sull'altezza
relativa all'ipotenusa è
equivalente al rettangolo che ha
per dimensioni le proiezioni dei
cateti l'ipotenusa stessa"
2
HB = AH x HC