Transistore ad effetto di campo (MOSFET)

Transistore ad effetto di campo (MOSFET)
1.1 Introduzione…...……………………………………………………………………….………...2
1.2 MOSFET ad arricchimento…..…………………………………………………………..…......3
1.3 Funzionamento...…………………………………………………………………………….…...5
1.4 VGS ≅ 0…………………………………………………………………………………….……..6
1.5 VGS > VTH e VDS < VDSsat……..………………………………………………………...……….7
1.6 VGS > VTH , VDS >VDSsat.………………………………………………………………….……...9
1.6 Simbolo Circuitale e Convenzione per Tensioni e Correnti……………………………..…..11
1.7 MOSFET a canale p ad arricchimento……………………………………………………….12
1.8 Tecnologia CMOS……………………………………………………………………….….….13
1.9
Curve caratteristiche del MOSFET (nel caso di MOSFET a canale n ad
arricchimento)…………………………………………………………………………….………...14
1.10 Modello in continua o ‘Ai grandi segnali ’ del MOS……………………………….….…..16
1.11 Transistore MOSFET a svuotamento……………………………………………….…….…21
1.12 Il MOSFET come amplificatore………………………………………………………….…..22
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 1
1 Introduzione
Il transistore ad effetto di campo (FET, Field Effect Transistor) è un componente a quattro terminali:
controllando la tensione applicata ad uno di essi (detto Gate) è possibile regolare il flusso di corrente fra
altri due morsetti (Source e Drain). Il transistore ad effetto di campo prende il nome dall’effetto fisico
su cui è basato: in particolare il controllo della conduzione nel canale avviene tramite l’applicazione di
un campo elettrico al nodo di controllo (Gate).
La conduzione avviene tramite un solo tipo di portatori di carica o lacune o elettroni, perciò il FET
prende anche il nome di transistore unipolare.
La tecnologia di realizzazione dei FET più utilizzata è chiamata MOS (Metal–Oxide–Semiconductor)
da cui il nome di MOSFET.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 2
1.2 MOSFET ad arricchimento.
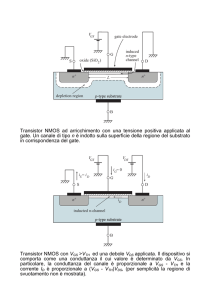
Fig. 1: vista d’insieme e sezione trasversale del MOSFET.
La struttura fisica ideale del MOSFET è qui descritta nella Fig.1(b): su di un substrato monocristallino
di tipo p, vengono realizzate due giunzioni di tipo n+ (1), a cui fanno capo due terminali chiamati drain e
source (D ed S in figura). Nella zona compresa fra drain e source viene fatto crescere uno strato di biossido di
silicio (spessore minore di 0.01 μm) che è un ottimo isolante.
(1) Nota :
n+ indica un drogaggio a concentrazione più elevata rispetto a quella di un drogaggio n.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 3
L’elettrodo di gate è realizzato in silicio policristallino.
Esiste inoltre un quarto terminale collegato al substrato body o bulk. (B in figura)
La zona all’interno del substrato compresa fra drain e source è detta canale (channel).
Per fare in modo che le due giunzioni di Source e di Drain non siano mai polarizzate direttamente, si
deve polarizzarle entrambe inversamente ovvero si deve fare in modo che il body sia collegato alla
tensione più bassa presente nel circuito.
Nella Fig. 1(a) sono mostrate le dimensioni del FET: Lenght e Width (i.e. L e W).
Oggigiorno le tecnologie a semiconduttore vengono individuate tramite la misura della lunghezza di
canale L. Valori tipici di L si aggirano intorno agli 0.18 μm, anche W ha misure dell’ordine di frazioni
di μm.
Il substrato invece ha uno spessore in proporzione molto maggiore: misure tipiche si aggirano intorno
alla frazione di mm (qualche centinaio di μm) ovvero circa 1000 volte più grande rispetto alla L del
canale anche se, in figura, non è evidenziato. Come si nota il substrato di tipo p forma con i due
terminali di drain e di source di tipo n+ due giunzioni pn che nel normale funzionamento sono sempre
tenute in interdizione (pol. inversa).
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 4
1.3 Funzionamento
Vediamo ora come avviene la conduzione del MOSFET ovvero il passaggio di corrente dal drain al
source, controllato tramite l’elettrodo di gate.
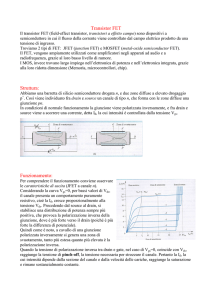
Fig. 2: Transistor n-MOS ad arricchimento in presenza di una tensione positiva sul Gate.
Chiamiamo VGS la tensione fra Gate e Source e VDS la tensione fra Drain e Source.
Mettiamo i terminali B, S, D a massa. Applichiamo una VGS >0 al terminale G:
Si determina un campo elettrico che in un primo momento allontana le cariche positive (lacune) dalla
regione di canale, aumentando la VGS, il numero di cariche negative (elettroni) (2) nella zona di
svuotamento aumenta progressivamente fino a raggiungere un numero uguale a quello che avevano le
lacune.
A questo punto abbiamo sostanzialmente invertito la carica nella regione di canale che è diventata
negativa. Abbiamo così realizzato è un condensatore che ha come armature: la regione di canale fra
source e drain ed il terminale di gate. Il dielettrico è lo strato di biossido di silicio (SiO2).
Riassumendo:
funzionamento condensatore
body a massa
drain e source alla stessa tensione (spesso a massa)
VGS > 0
In questa configurazione si può notare che aumentando da zero la tensione di gate si raggiunge prima
uno stato in cui il numero di elettroni nel canale è pari a quello delle lacune che erano presenti in
condizioni di riposo, il valore di VGS in questo stato e chiamato tensione di soglia VTH. In questo stato
il canale si è appena formato e vi scorre una corrente trascurabile. Per valori di VGS superiori alla soglia
il canale incomincia ad allargarsi.
E’ chiaro ormai che affinché il MOSFET conduca deve essere indotto (induced) un canale per questo il
MOSFET che stiamo analizzando si dice ad arricchimento (enhancement).
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 5
Nota :
anche se non l’abbiamo ancora detto all’interno del FET scorre comunque una corrente
anche per valori VGS sotto soglia perché nel canale stazionano sempre alcuni elettroni
di conduzione. Noi in ogni caso considereremo la corrente sotto soglia come nulla
(trascurabile)
Nota:
la VTH dipende da caratteristiche tecnologiche del componente; di solito oscilla fra
0.5V e 3 V.
1.4 VGS ≅ 0 V
Chiediamoci ora cosa succederebbe se non applicassimo alcuna tensione al gate:
il transistor si ridurrebbe a due diodi in serie collegati fra drain e source che non permetterebbero alcuna
circolazione di corrente fra i due terminali anche in presenza di una VDS piuttosto elevata. La resistenza
fra drain e source in questo caso è dell’ordine di 1012 Ω ovvero la zona di canale si potrebbe assimilare
ad un circuito aperto.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 6
1.5 VGS > VTH e VDS < VDSsat
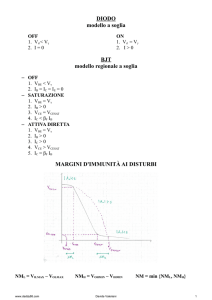
Fig. 3: Tensione n-MOS a cui sono applicate una VGS >VTH ed una VDS≈0
Colleghiamo il B a massa, applichiamo una VDS piccola al terminale D (qualche centinaio di mV) ed
applichiamo una VGS al terminale di G.
Ci troviamo ora in presenza di due campi elettrici : uno fra gate e canale e l’altro, che viene indotto
dall’applicazione di VDS, fra source e drain.
Il campo indotto da VDS fa scorrere gli elettroni all’interno del canale da source (sorgente) a drain
(pozzo) ovvero per convenzione scorre una corrente da drain a source che chiameremo ID proporzionale
al n° di elettroni e di verso opposto al loro moto.
Questa corrente è proporzionale alla tensione di gate che controlla il numero di elettroni nel canale.
Questa proporzionalità ci induce a pensare di trovarci in presenza di un resistore la cui conduttanza
dipende dallo spessore del canale ovvero dalla tensione di gate VGS. Aumentando la tensione di gate
allarghiamo il canale e ne diminuiamo quindi la resistenza, viceversa se diminuiamo VGS la resistenza
aumenta progressivamente.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 7
I D(mA)
0,8
VGS=Vt +8V
0,6
VGS=Vt +6V
VGS=Vt +4V
0,4
VGS=Vt +2V
0,2
0
50
100
150
200
VDS(mV)
Fig. 4: Caratteristica ID - VDS.
Mettiamoci nella condizione VGS > VTH .
La conduttanza del canale GC dipende dalla differenza fra VGS e VTH .
GC ∝ VGS − VTH
Se si rappresenta graficamente l’andamento della ID in funzione della VDS parametrizzando su VGS
ovvero tenendo costante VGS per ogni escursione di VDS da zero al suo massimo valore (200 mV in
figura) , si ottiene una famiglia di curve che rappresenta la caratteristica di un resistore lineare
controllato in tensione VGS .
Sul grafico possiamo leggere che all’aumento della iD a parità di VDS corrisponde ad una diminuzione
della resistenza di canale (ricordiamo che la conduttanza è pari alla pendenza della retta:
G = I /V
Riassumendo:
funzionamento resistore
body e source alla stessa tensione (spesso a massa)
VDS ≈ 0 piccola (0.1 – 0.2 V)
VGS > 0
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 8
1.6 VGS > VTH , VDS >VDSsat
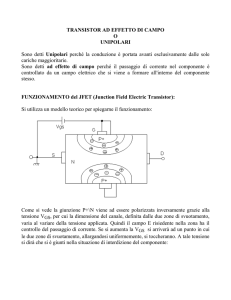
Fig. 5: Funzionamento del FET n-MOS per tensioni VDS più grandi.
Ora mettiamoci nel caso in cui VDS non sia più piccola e VGS sia costante e maggiore di VTH quindi
cominciamo ad aumentare la tensione VDS e verifichiamo che il canale progressivamente si restringe
verso il terminale D. All’aumento della VDS anche la resistenza del canale aumenta.Questo significa
che spostandosi sul canale dal source al drain la tensione VDS aumenta da zero a VDS. Questo implica
che la tensione di gate VGS, debba diminuire da VGS a VGS - VDS, e che quindi il canale assuma la
forma rappresentata in figura. Il canale si stringe fino ad un punto di strozzamento (pinch-off) in cui
anche se si aumenta la tensione VDS il passaggio di corrente ID non aumenta più linearmente, anzi si
stabilizza ad un valore di saturazione. Chiameremo il valore di tensione VDS per cui si è raggiunto il
sat
punto di pinch-off: VDS .
sat
DS
GS
TH
V
= V −V
Fig. 6: Curva della ID in funzione della VDS (con VGS >VTH).
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 9
Nella zona di saturazione il MOSFET si comporta come un generatore di corrente controllato tramite la
tensione applicata al gate.
Il punto di passaggio fra zona triodo (lineare) e zona saturazione si ha quando :
sat
DS
DS
.
V
=V
Tabella riassuntiva
A seconda del valore di VGS ci troviamo nelle diverse zone di lavoro
Valore di VGS
VGS < VTH
VGS > VTH e VDS < VDS
Zona di lavoro
Interdizione
sat
VGS > VTH VDS >VDSsat
Triodo / lineare
Saturazione
Caratteristiche
resistore controllato in
tensione VGS con
caratteristica lineare per
valori di VDS piccoli.
generatore di corrente
pilotato in tensione VDS
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 10
1.6 Simbolo Circuitale e Convenzione per Tensioni e Correnti
D
D
VGD
G
G
VDS = VGS - VT
VGS
S
S
Fig. 7:
Simbolo circuitale del MOSFET a canale n e relativa esemplificazione delle tensioni.
La freccia sul terminale S indica il verso positivo della corrente di canale.
Si noti che il terminale B è stato omesso per il fatto che si assume lo si colleghi sempre
alla tensione più bassa del circuito.
Nella conduzione all’interno del MOSFET a canale n soltanto gli elettroni contribuiscono alla
conduzione.
Il MOSFET, a differenza del transistor bipolare che ha impedenza di ingresso (e.g. di base) finita e
dipendente dalle caratteristiche costruttive del componente e dalle condizioni di polarizzazione, ha
impedenza di ingresso infinita in corrente continua in quanto i terminali di ingresso fanno capo ad un
condensatore e fra le armature di un condensatore scorre una corrente nulla
Z =V /I
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 11
1.7 MOSFET a canale p ad arricchimento
La tecnologia ha sviluppato, dualmente al MOSFET a canale n, il MOSFET a canale p.
Esso ha caratteristiche duali rispetto al tipo n, il body è drogato con impurità di tipo n mentre le
giunzioni di S e D sono di tipo p+; affinché le giunzioni siano sempre in polarizzazione inversa è
necessario che venga collegata al body la tensione più alta del circuito.
La conduzione è affidata alle lacune.
S
G
D
Fig. 8: Simbolo del MOSFET a canale p ad arricchimento.
Se manteniamo come verso di percorrenza positivo della corrente il verso da D a S la corrente che
scorre nel MOSFET a canale p è negativa (iD < 0 ) e di conseguenza anche la VDS, la VGS e la VTH
sono negative .
Valgono esattamente tutti i ragionamenti fatti per il MOSFET a canale n con tutti i segni invertiti.
Anche se la tecnologia p-MOS è stata soppiantata dalla n-MOS che richiede una più bassa tensione di
alimentazione ed è più veloce, si continuano ad utilizzare i p-MOS in particolari circuiti a componenti
discreti e soprattutto in quella che si definisce tecnologia CMOS (Complementary MOS ).
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 12
1.8 Tecnologia CMOS
Fig. 9: Sezione trasversale di un circuito integrato CMOS.
La tecnologia CMOS permette di costruire su di uno stesso “wafer” di silicio sia transistori di tipo pMOS che transistori di tipo n-MOS.
I p-MOS sono direttamente realizzati sul wafer mentre per gli n-MOS si ricorre ad una tecnica nota
come pozzo (well ). In figura è mostrato un pozzo p: nel substrato di tipo n si costruisce una zona
drogata positivamente sulla quale realizzare il transistor n.
Accanto alla realizzazione pozzo p (p – well), esiste anche quella di tipo n – well.
Nota :
Nel transistore bipolare si individuano immediatamente i terminali B, C, E perché sono
individuati al momento della fabbricazione, nel MOSFET invece fino a polarizzazione
avvenuta non si può sapere quale sia il source o il drain perché costruttivamente sono
identici.
Nota :
Sappiamo che è necessario collegare il body alla tensione più bassa del circuito affinché
le due giunzioni di S e D siano polarizzate inversamente, questo non risulta essere un
problema quando parliamo di componenti discreti perché possiamo tranquillamente
collegare i body dei singoli MOSFET alla tensione che preferiamo di solito quella del
source. Se parliamo invece di componenti integrati siamo nella situazione di più
transistors sullo stesso wafer quindi a bulk comune : in questa situazione non è più
pensabile collegare tutti i source in comune al body quindi si ricorre alla tecnologia
CMOS : per esempio costruendo un pozzo per ciascun transistore.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 13
1.9 Curve caratteristiche del MOSFET (nel caso di MOSFET a canale n ad
arricchimento).
iD
iG = 0
+
VDS
+
D
VGS
i S = iD
-
-
Fig. 10: Circuito per ricavare le caratteristiche e caratteristica ID-VDS
Per ricavare la famiglia di caratteristiche iD, VDS con parametro VGS basta tenere fissa la VGS e far
variare la VDS ottenendo una curva a VGS costante.
Se ripetiamo per ogni VGS questa operazione otteniamo l’intera famiglia di curve.
Sul grafico possiamo individuare le tre zone di funzionamento del MOS a canale n che abbiamo già
visto al paragrafo 6.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 14
Valore di VGS
VGS < VTH
VGS > VTH e VGD >
VTH
VGS > VTH e VDS <
VDSsat
Zona di lavoro
Interdizione (cut-off)
Triodo
Utilizzo
Interruttore
Interruttore
Saturazione
Amplificatore
Come si vede nella tabella per poter lavorare in zona triodo dobbiamo prima indurre un canale e quindi
mantenerlo facendo in modo che
VGD > VTH .
Se volessimo vedere questa relazione in funzione di VDS potremmo scrivere che :
VGD = VGS + VSD = VGS − VDS
da cui otteniamo
VGS − VDS > VTH
VDS < VGS − VTH
ovvero il MOS è in triodo se VGS è maggiore della soglia e la tensione di D è più bassa di quella di G di
almeno la soglia VTH .
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 15
1.10 Modello in continua o ‘Ai grandi segnali ’ del MOS.
L’analisi in continua corrisponde all’analisi in bassa frequenza; questo implica che sia le capacità
intrinseche del MOS, sia le capacità di disaccoppiamento vengano considerate rispettivamente come
degli aperti e come dei corti-circuiti.
Zona Triodo / Lineare
Se sono verificate le condizioni di cui al paragrafo precedente ci troviamo in zona triodo (zona lineare).
La linearità dipende dal valore della tensione VDS, più VDS è piccola più la linearità è rispettata.
Possiamo scrivere la caratteristica del MOS in zona triodo con la seguente espressione:
[
iD = K 2(VGS −VTH)VDS −VDS 2
K=
] (1)
1
⎛W ⎞ ⎡ A ⎤
μnCOX ⎜ ⎟ → ⎢ 2 ⎥
2
⎝ L ⎠ ⎣V ⎦
Dove:
μn : mobilità dell’elettrone
COX : capacità dell’ossido per unità di area, capacità fra G e Bulk o meglio fra G e canale.
C OX =
Nota :
Nota :
ε OX / t OX
εOX : costante dielettrica dell’ossido di silicio ≈ 3.45 10-13 [F / cm]
tOX : spessore dell’ossido sottile fra canale e G.
μn
dipende dal drogaggio della zona relativa al canale e dalla temperatura di esercizio
del dispositivo. In questo caso ci riferiamo ai portatori di carica di tipo n, ovvero agli
elettroni che hanno una mobilità maggiore delle lacune. In particolare μn ≈ 3 μp a parità
di campo elettrico.
Proprio a causa di questa differenza fisica i dispositivi n-MOS sono più veloci e quindi
preferibili a quelli di tipo p.
2
Se analizziamo la (1) ci rendiamo conto che abbiamo una dipendenza dalla VDS però se
2
la VDS è piccola la VDS è trascurabile e questo implica che la (1) diventi:
iD ≈ 2 K [(VGS − VTH )VDS ] (2)
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 16
Nota :
Se fissiamo la VGS otteniamo che la ID risulta proporzionale alla VDS e che quindi, in
zona triodo il MOS è approssimabile ad un resistore di valore:
rDS ≈
VDS
1
≈
IDS [2 K (VGS − VTH )]
(valevole per VDS piccole)
Zona Saturazione (Facendo sempre riferimento alla Fig.10)
Creiamo un canale, ovvero imponiamo:
VGS ≥ VTH
strozziamolo in prossimità del Drain facendo in modo che VDS sia tale che
VGS ≤ VTH
ovvero, in termini di VDS:
VDS ≥ VGS − VTH = VDS
sat
Il MOSFET quindi lavora in saturazione quando la VGS è maggiore della soglia e VD non è mai più
bassa di VG di una quantità pari a VTH.
sat
Noto che VDS è il valore di VDS per cui dalla zona triodo si passa in quella lineare, la corrente
corrispondente si ricava sostituendo nella (1) la VDS
sat
ottenendo :
sat
i D = K (VGS - VTH ) 2 (3)
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 17
iG = 0
iD
G
D
+
+
VGS
K (VGS - VTH)2
-
VDS
-
S
Fig. 11: Caratteristica ID-VGS e circuito equivalente ai grandi segnali del MOSFET n in
saturazione
Come si vede sulle caratteristiche, Fig.10, la corrente ID perde la sua proporzionalità rispetto alla VDS
uscendo dalla zona triodo, quindi la corrente ID non dipenderà più dalla VDS ma soltanto dalla VGS
come si vede nella (3) .
Il MOSFET si comporta come un generatore ideale di corrente pilotato in tensione.
Zona di Interdizione
Il transistore (canale n ad arricchimento) è interdetto se la tensione al gate è sotto soglia (cut off), fra le
caratteristiche di Fig.10 si può identificare quella per cui si ha interdizione con quella ad iD nulla.
Il modello che abbiamo dato del MOSFET non è molto accurato perché abbiamo trascurato che
sat
comunque, in saturazione, la iD dipende sempre dalla VDS: ovvero se la VDS aumenta più della VDS
il punto di pinch-off (strozzamento) si sposta un po’ verso il Source, dando luogo ad un effetto chiamato
modulazione di lunghezza di canale.
Fig. 12: Modulazione della lunghezza di canale.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 18
Questo effetto si può sintetizzare modificando la (3) così :
i D = K (VGS - VTH ) 2 (1 + λVDS ) (4)
sat
Dopo questa modifica accade che la pendenza delle caratteristiche non è perfettamente orizzontale e si
scopre che le rette tangenti alle caratteristiche in saturazione passano per lo stesso punto
1⎞
⎛
0
,
−
⎜
⎟ .(2)
(0,−VA) o
λ
⎝
⎠
Gli effetti della modulazione di lunghezza di canale si evidenziano nel fatto che la resistenza di uscita
del MOSFET non si può più considerare idealmente infinita ma essa è finita e si può misurare come la
pendenza delle caratteristiche ovvero:
−1
⎡ ∂i ⎤
rO ≡ ⎢ D ⎥
⎣ ∂VDS ⎦ VGS =cos t .
e quindi:
[
rO = λK (VGS − VTH ) 2
che possiamo approssimare con:
]
−1
rO ≈ [λI D ]
−1
Dove ID è la corrente corrispondente al particolare valore di VGS per cui rO è stato calcolato.
In questa espressione si sono trascurati gli effetti su r0 del termine
(1 + λVDS )
della (4).
Questa ultima espressione è scrivibile alternativamente nella forma:
rO ≈ V A / I D
Come si vede più si aumenta la ID più la rO diminuisce.
(2) I valori di λ si aggirano nell’intervallo [10-2 ÷ 10- 3] V-1 quindi i valori corrispondenti di VA saranno [102 ÷ 10 3] V
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 19
Il modello circuitale del MOSFET risulta essere il seguente:
iG = 0
iD
G
D
+
+
VGS
r0
2
VDS
-
K (VGS - VTH)
S
Fig. 13: Modello ai grandi segnali che tiene conto della modulazione della lunghezza di canale.
Nota :
Tutto quello che si è visto per il transistore n-MOS vale dualmente per il p-MOS.
Nota :
Un fenomeno che si può manifestare nei FET è il breakdown , l’effetto di breakdown si
verifica quando applichiamo al Gate una tensione più alta di quella che il suo dielettrico
(SiO2) può sopportare. (max 50V che è la tensione di rottura del SiO2 )
Questo effetto (breakdown) è aggravato dal fatto che l’impedenza di ingresso del MOSFET è infinita.
L’impedenza infinita di ingresso facilita l’accumulo di cariche statiche sull’elettrodo di gate facendogli
raggiugere anche tensioni di valore elevato, si raggiunge facilmente la tensione di rottura del biossido di
silicio (SiO2).
Per evitare questo problema sono necessari dei circuiti di protezione del gate, realizzati sempre con
diodi.
D2
D1
VDD
Fig. 14:
Stadio di protezione al PAD (piedino) del Gate, la tensione di ingresso non può mai
superare la tensione di alimentazione VDD o scendere sotto la tensione di massa di un
fattore pari alla soglia dei diodi.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 20
1.11 Transistore MOSFET a svuotamento.
S
G
D
Fig. 15: Simbolo del MOSFET a svuotamento
Si tratta di un MOS che, dualmente a quello che abbiamo preso in esame, possiede sempre un canale
anche per tensioni VGS nulle.
Anche per VGS nulla se applicassimo una VDS positiva la corrente che scorrerebbe nel canale non
sarebbe nulla; contrariamente applicando una VDS negativa si restringerebbe il canale fino ad annullarlo
ovvero sino ad interrompere il passaggio di corrente al suo interno.
Nota: I MOSFET a svuotamento costruttivamente richiedono un arricchimento (drogaggio ) della zona
di canale, comportando dei costi di produzione maggiori.
Fig. 16(a): Caratteristiche iD – VDS, dell’n MOS a svuotamento.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 21
Fig. 16(a): Caratteristiche iD – VGS in saturazione dell’n MOS a svuotamento.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 22
1.12 Il MOSFET come amplificatore.
Sebbene per continuità non abbandoneremo il FET a canale n ad arricchimento tutto ciò che diremo nei
suoi riguardi può essere esteso a tutti gli altri tipi di FET.
Faremo ora una analisi grafica delle caratteristiche di un amplificatore a FET.
VDD = 20V
ID
vgs
+
VGS = 5V
-
+
vGS = 5V
-
RD = 1,33K
+
vDS
-
Fig. 17: Circuito di polarizzazione e andamento del segnale VGS (dente di sega di ampiezza 1 Vpp).
Fig. 18: Analisi grafica del FET come amplificatore.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 23
Come si vede nella Fig. 17 il FET è polarizzato in continua tramite una VGS (5V in figura), al gate
inoltre giunge il segnale vgs (componente ai piccoli segnali), il Drain è collegato all’alimentazione
positiva tramite la resistenza RD (resistenza di carico), il Source è a massa;
quindi al Gate complessivamente giunge una tensione istantanea pari a :
v GS = VGS + v gs
applicando le leggi di Kirchoff alla maglia
v DS - R D - V DD si ricava che:
v DS = VDD - R D i D
ovvero ricavando la iD :
i D (t ) =
VDD v DS (t )
−
RD
RD
Questa espressione sul piano (iD-vDS) risulta essere una retta che chiameremo retta di carico, essa
interseca gli assi a VDD e VDD / RD.
Fissare la vGS sul piano iD-vDS significa fissare una delle caratteristiche.
Il punto di intersezione fra la retta di carico e la caratteristica scelta è il punto di lavoro (bias point).
E’ importante notare che la retta di carico non è un attributo del transistor, come lo sono le
caratteristiche, ma è del tutto generale.
Iniziamo la vera e propria analisi grafica: applichiamo al Gate del transistore, polarizzato in continua da
VGS, un segnale vgs. Tramite il circuito esterno e la RD (resistenza di carico) definiamo la retta di
carico ed il punto di lavoro che come sappiamo è all’intersezione della retta di carico con la
caratteristica fissata da VGS. Nel nostro caso sceglieremo la caratteristica a VGS = 5V e di
conseguenza un punto di polarizzazione in continua o di riposo Q.
Quando si applica l’onda triangolare vgs, il punto di lavoro si muove da Q sulla retta di carico
seguendo l’andamento della tensione complessiva al Gate vGS che, come sappiamo, è la somma della
tensione di polarizzazione in continua e del segnale vgs.
Sul terminale di uscita (Drain) si ritroverà una componente di corrente statica ID e una variabile iD
che ricopierà quella di ingresso, in generale con ampiezza e fase diversa, nel nostro caso l’ampiezza è
otto volte maggiore del segnale di ingresso e lo sfasamento è di centottanta gradi (inversione di fase).
Come si nota il comportamento del FET è pressoché lineare nella zona di saturazione, non lo è
assolutamente in triodo o in interdizione quindi per non introdurre distorsioni è necessario che il punto
di lavoro di riposo Q sia ben centrato nella zona di saturazione.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 24
Vediamo nella Fig.19 che cosa succederebbe se Q fosse spostato più verso la zona triodo (situazione
che si ottiene aumentando la resistenza di carico RD ).
Fig. 19 : Caso di distorsione non lineare causata dall’erroneo posizionamento del punto Q.
Come si vede qui in figura, sebbene il punto di lavoro statico Q sia in saturazione, il punto di lavoro
dinamico grazie alle variazioni del segnale di ingresso può entrare nella zona triodo e quindi portare ad
una distorsione del segnale.
Vediamo come ricavare dal punto di vista matematico un modello ai piccoli segnali del transistore.
Sappiamo che la tensione totale applicata al Gate è data da:
vGS = VGS + v gs
In continua (vgs
=0):
i D = K (vGS − VTH ) 2
VDS = VDD − RD I D
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 25
Se applichiamo vgs invece :
i D (t ) = K (vGS − VTH ) 2 = K (VGS + v gs − VTH ) 2 =
= K (VGS − VTH ) 2 + 2 K (VGS − VTH )v gs + Kv gs
2
(1)
Il primo addendo è pari alla ID di polarizzazione, mentre il secondo addendo è un termine costante
dipendente da VGS mentre il terzo addendo è un termine di distorsione non lineare.
Vorrei fare in modo di ridurre la distorsione non lineare quindi faccio una ipotesi ovvero che il segnale
vgs sia un ‘piccolo segnale ’ cioè:
v gs << (VGS − VTH )
e quindi trascurare il secondo e terzo addendo della (1) a fronte del primo:
i D ≈ I D + id
dove
id , corrente di segnale è data da :
id = 2 K (VGS − VTH )v gs .
Come si vede la relazione che lega
id
e
gm ≡
v gs
è una costante (transconduttanza gm):
id
= 2 K (VGS − VTH )
v gs
quindi :
id = g m v gs
Fig. 20 :
Interpretazione grafica del funzionamento del MOSFET ad arricchimento ai piccoli
segnali: gm è uguale alla pendenza della caratteristica iD - vGS nel punto di lavoro.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 26
Come si vede in figura gm rappresenta la pendenza della caratteristica ovvero :
gm ≅
∂i D
∂v GS
= 2 K (VGS − VTH )
vGS =VGS
quindi la transconduttanza si ricava graficamente sulla caratteristica iD - vGS tracciando la tangente nel
punto di lavoro.
Nota :
K è dell’ordine di
⎡ mA ⎤
⎢⎣ V 2 ⎥⎦ per circuiti a componenti discreti e di
⎡ μA ⎤
⎢⎣V 2 ⎥⎦ per circuiti
integrati)
Sostituendo a K la sua espressione che abbiamo trovato al paragrafo 10 si ottiene:
⎛W
g m = ( μ n C OX )⎜
⎝L
diversamente sostituendo a (VGS-VTH) l’espressione
⎞
⎟(VGS − VTH )
⎠
ID
si ottiene:
K
g m = 2 μ n C OX W / L I D
Nota :
confronto con il transistore bipolare
L’espressione della gm nel transistore bipolare è:
I
βI
gm = C = B
V BE V BE
si noti che per il transistore bipolare l’espressione di gm non dipende dalle
dimensioni geometriche (W e L) del componente.
Quindi nel transistore bipolare a parità di corrente la transconduttanza è
maggiore che nel MOS.
Proviamo ora a calcolare il guadagno in tensione AV del MOSFET ai piccoli segnali.
Possiamo scrivere la tensione complessiva, componente di polarizzazione più componente ai piccoli
segnali, al drain in questo modo:
v DS = V DD − R D i D
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 27
Nell’ipotesi di piccoli segnali si ha che:
v DS = V DD − R D ( I D +i d )
ovvero nel punto di lavoro statico:
v DS = V DD − R D I D
quindi la componente di segnale della tensione di drain risulta essere :
v ds = −i d R D = − g m R D v gs
dalla quale si deduce che il guadagno di tensione AV ai piccoli segnali è dato da :
AV =
vd
= − g m RD
v gs
ovvero che l’amplificatore è invertente (sfasamento di 180° fra il segnale di ingresso e quello di uscita)
cosa che si esplica nel segno meno dell’espressione sopra e che si vede in Fig.21.
Fig. 21 : Relazione fra il segnale di ingresso e segnale di uscita nel MOSFET (circuito di Fig.17)
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 28
Abbiamo fino qui ipotizzato che, in saturazione, la corrente di drain sia indipendente dalla tensione di
drain mentre invece sappiamo che a causa dell’effetto della modulazione di lunghezza di canale questo
non è vero quindi in prima approssimazione possiamo dire che il transistore MOS si comporta come un
generatore ideale di corrente (gmvgs) controllato in tensione (vgs) il cui modello ai piccoli segnali è in
Fig.22(a). Dobbiamo però tenere conto della dipendenza fra id e vd quindi introdurre un modello di
questo effetto ottenuta in Fig.22(b) tramite la resistenza a valore finito (molto grande) ro (si riveda il
paragrafo 11).
D
G
G
gmVgs
+
D
+
VGS
VGS
-
-
gmVgs
R0
S
S
(a)
Fig. 22 : Modello ai piccoli segnali del MOSFET.
(b)
Come abbiamo visto al paragrafo 11 l’espressione della corrente di Drain risulta :
I D = K (VGS - VTH ) 2 (1 + λVDS )
quindi ID dipende anche da VDS per cui possiamo definire :
∂I D
1
g0 =
=
r0 ∂V DS
Q
≅ λI D0
-1
dove l’ apice 0 sta ad indicare che ID e VDS sono calcolate per λ = 0 [V ] (caso ideale).
In altri termini :
r0 =
1
dove
λ
= VA
VA
1
1
≅
=
g 0 λI D 0 I D0
è un parametro tecnologico del transistore (non si confonda VA con AV (guadagno in
tensione)).
Di conseguenza il guadagno in tensione diventa:
AV = − g m ( R D // r0 ) .
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 29
1.13 Interruttore MOS
+
Vc = Max+7V
Min -3V
G
VTH=2V
IG = 0
V0
+
B
Va = Max +5V
Min -5V
-
RL
CL
-5V
Fig. 23
Il dispositivo in figura mostra un circuito che sintetizza un interruttore utilizzando un transistore NMOS. A priori non conosciamo quale sia il piedino di source o di drain.
Il source è per definizione la giunzione con la tensione più bassa rispetto al drain.
A titolo di esempio (utile per comprenderne il funzionamento) supponiamo
VTH = 2V
Inoltre considereremo il condensatore
CL
inizialmente scarico.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 30
Caso1)
Vc = +7V ⎫
⎬ → allora → V0 = +5V
Va = +5V ⎭
VCC = +5V
a
b
V0 =+5V
+
Vc = 5V
RL
-
CL
Fig. 24
Come si vede dalla figura (subito sopra) imponendo le tensioni Va e Vc e avendo ipotizzato che il
condensatore C L sia scarico il morsetto ‘a’ del MOS sarà il drain mentre il morsetto ‘b’ sarà il
source poiché è il morsetto ‘a’ è a tensione superiore del morsetto ‘b’.
Se alzassimo ulteriormente la
Va sopra i 5V la tensione Vo non potrà mai salire oltre il valore 5V
Questa caratteristica deriva dal fatto che la tensione Vc è stata fissata a +7V quindi tenendo conto
della tensione di soglia ( VTH = 2V), anche aumentando Va sopra i 5V, la tensione VGS
sarebbe superiore a 0 e non ci sarebbe canale (il MOS si troverebbe in interdizione).
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 31
− VTH
non
Caso2)
Vc = +7V ⎫
⎬ → allora → V0 = −5V
Va = −5V ⎭
Va = -5V
a
b
V0 =-5V
+
VC = 7V
RL
-
CL
Fig. 25
Come si vede dalla Fig.25 al contrario del caso precedentemente visto, supponendo il condensatore
CL
scarico, il morsetto ‘a’ del MOS è alla tensione più bassa rispetto al nodo ‘b’. In questo caso il
source del MOS è il nodo ‘a’ mentre il nodo ‘b’ è il drain.
In questo caso anche rendendo più negativa la tensione
accadeva nel caso precedente poiché
negativo di
VGS − VTH
Va
non ci sarebbe alcuna limitazione, come
è sempre maggiore di zero qualsiasi sia il valore
Va .
Riassumendo le tensioni positive vengono limitate cosa che non accade per quelle negative.
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 32
1.14 Interruttore C-MOS
+5V
VC = Max +5V
Min -5V
canale p
VTH =2V
+
vC
v0
+
+
vA
-
vC
RL
CL
canale n
-5V
Fig. 26
In Fig.26, sono stati utilizzati due MOS complementari come interruttori : questo circuito è
comunemente conosciuto con il nome di “trasmission gate” ovvero porta di trasmissione.
Il trasmission gate è formato da un interruttore N-MOS e da uno P-MOS collegati come in figura, è
inoltre interessante notare che le tensioni sui gate sono due tensioni complementari indicati con Vc
e V c ovvero
Vc = −V c
La parte inferiore del circuito è già stata analizzata, la parte superiore funziona analogamente.
Da quanto detto sull’interuttore N-MOS e ragionando analogamente per il transistore P-MOS, questo
circuito sarà un perfetto interruttore privo di limitazione in tensione in quanto l’interruttore N-MOS
non limita le tensioni negative ed il P-MOS non limita quelle positive.
(ciò non accade se si considera un interruttore N-MOS o un P-MOS analizzati ‘singolarmente’).
Transistore ad effetto di campo (MOSFET)
Prof. Maurizio Valle
A.A. 2006 – 2007 pag. 33