1. Il "teorema di Pitagora" non è di Pitagora
Su una tavoletta d'argilla, ritrovata tra le rovine di una città della Mesopotamia e risalente al periodo
paleobabilonese della dinastia Hammurabi (1800 - 1600 a. C.), è disegnato un quadrato e le sue diagonali.
Su un lato è riportato il numero 30 e su una diagonale i numeri 1,414213... e 42,42639..., tutti numeri
espressi nel sistema sessagesimale, quello usato dai Babilonesi.
Il primo dei due numeri, sulla diagonale, è un valore
approssimato, ma già molto preciso, della radice di 2, l'altro è la
diagonale del quadrato, cioè il prodotto di 30 per questo numero.
Un calcolo che molti lettori sicuramente conoscono e che
rivedremo poco più avanti. Un calcolo che prevede la conoscenza
del teorema di Pitagora.
Questa tavoletta (Fig. 1), che oggi
è conservata negli Stati Uniti,
all'Università
di
Yale,
all'apparenza un ciottolo largo
appena una decina di centimetri,
storicamente è importantissima.
George Gheverghese, lo storico
Fig. 1 La tavoletta di argilla con il calcolo della
diagonale di un quadrato
indiano della matematica, la
definisce
"un
capolavoro
babilonese" e viene riportata in tutti i testi di storia della matematica, come
prova del fatto che il teorema di Pitagora era già noto almeno mille anni
prima di Pitagora. Vale a dire che il teorema di Pitagora ... non è di Pitagora.
Se ne trovano tracce in molti altri documenti non solo babilonesi, ma di
altre civiltà, ad esempio dell'Antica Cina o dell'India, ben prima della
Fig. 2 Pitagora di Samo, 580-500 a.C.
nascita di Pitagora. Se noi siamo portati a privilegiare e a mettere in primo
piano la civiltà greca, è soltanto perché questa è alle radici del nostro pensiero, della civiltà occidentale.
In generale possiamo dire che è molto difficile, sovente
impossibile, risalire all'origine delle idee matematiche. Queste
non sono patrimonio di un'unica civiltà e tantomeno di un solo
uomo. Per fortuna, a nessuno, finora è venuto in mente di
brevettare un teorema, come accade invece regolarmente per
metodi e procedimenti che industrie chimiche, informatiche e di
tanti altri settori si affrettano a brevettare, per garantirsi
l'esclusiva di tutti i possibili sfruttamenti commerciali. Le idee
della matematica appartengono a tutta l'umanità, nascono
sovente nello stesso periodo, in ambienti diversi, e si precisano e
si arricchiscono con il contributo di più persone, a dimostrazione
Fig. 3 Pitagora su una moneta greca
del fatto che la matematica è la vera scienza universale e
sicuramente
la
più
democratica.
Ne abbiamo una prova proprio con il teorema di Pitagora.
Furono soltanto i pitagorici ad attribuirlo a Pitagora, obbedendo alle loro regole, secondo le quali si doveva
attribuire al maestro ogni scoperta, e questo anche dopo la sua morte, perché era sempre lui ad ispirare e
guidare qualsiasi lavoro. Il suo merito o più probabilmente di qualcuno dei suoi discepoli, è stato quello di
averne dato una dimostrazione rigorosa e più in generale di aver avviato un'analisi approfondita dei
principi sui quali si fonda il pensiero matematico.
2. Pitagora e i pitagorici
Pitagora (quando useremo questo nome, si tenga presente che non indicheremo soltanto Pitagora, ma la
sua scuola poiché, come abbiamo detto, è impossibile distinguere i suoi lavori da quelli degli altri
pitagorici) segna il momento di passaggio dalla matematica applicata alla matematica astratta, con
l'introduzione di dimostrazioni fondate sul metodo deduttivo a partire da assiomi esplicitamente
formulati. Afferma Bertrand Russell:
Dal punto di vista intellettuale, Pitagora è uno degli uomini più notevoli che siano mai esistiti, sia per la
sua sapienza sia per altri aspetti. La matematica, intendendo come tale le dimostrazioni e i ragionamenti
deduttivi, comincia con Pitagora. Non conosco altro uomo che abbia avuto altrettanta influenza nella
sfera del pensiero.
Pitagora nacque a Samo, un'isola della Ionia, nel 580 a. C. Quando
aveva circa quarant'anni, dopo essere stato allievo di Talete e dopo
aver visitato molti paesi, in particolare Egitto e Babilonia, abbandonò
la sua patria per sfuggire alla dittatura di Policrate e si stabilì a
Crotone, in Calabria, dove fondò una comunità filosofica e religiosa
che si impegnò direttamente nell'attività politica della regione.
Alla fine del sesto secolo, una sommossa, guidata dai nobili locali,
cacciò i pitagorici da Crotone. Pitagora si rifugiò a Metaponto dove
poco dopo morì. Sulla sua fuga da Crotone abbiamo una
testimonianza di Porfirio, un filosofo greco discepolo di Plotino:
Dopo la sua sconfitta si rifugiò nel porto di Caulonia e poi si diresse a
Locri, dove gli furono mandati incontro, ai confini del territorio, alcuni
anziani. Trovatolo, gli dissero: "Sappiamo, o Pitagora, che tu sei uomo
saggio e intelligente, ma noi siamo contenti delle nostre leggi e vogliamo
che restino così come sono, tu dunque se hai bisogno di qualcosa, prendila,
ma vattene altrove". In questo modo fu allontanato da Locri; di lì passò a
Taranto, dove ebbe la stessa sorte che aveva avuto a Locri e quindi passò a
Metaponto.
Fig. 4 Talete, circa 640 - 546 a. C. E' stato
probabilmente uno dei maestri di Pitagora.
Inizia con lui il processo di astrazione della
matematica.
I suoi seguaci crearono in seguito nuove comunità, nel nome del maestro, venerato come un dio. Le più
celebri furono quella di Tebe, fondata da Filolao, e quella di Taranto, fondata da Archita. La vita di
Pitagora, del quale non è rimasto alcun scritto, diventò ben presto leggenda e non è possibile avere notizie
certe su di lui.
Sappiamo che predicava l'astinenza e che imponeva ai discepoli una serie di regole e precetti dal valore
simbolico e rituale, come la proibizione di mangiare fave, di spezzare il pane, di toccare galli bianchi, di
attizzare il fuoco con il ferro o di accogliere rondini sotto il proprio tetto. Pitagora credeva nella
metempsicosi, ovvero nella trasmigrazione delle anime con successive reincarnazioni dell'anima in specie
diverse, fino alla loro eventuale purificazione e alla conseguente uscita dalla "ruota delle nascite". Lo studio
della matematica era visto come lo strumento per raggiungere questa liberazione dell'anima dal corpo:
numeri e forme della matematica, con la loro intrinseca bellezza e perfezione, sostenevano i pitagorici,
possono guidare l'anima verso il cielo.
In astronomia i pitagorici ritenevano che esistesse un grande fuoco centrale attorno al quale ruotavano
dieci corpi: la Terra, L'Antiterra, per noi invisibile, la Luna, il Sole, i cinque pianeti allora conosciuti e il
cielo delle stelle fisse. Questi corpi celesti nel loro movimento, secondo i pitagorici, producevano
un'armonia meravigliosa che noi non riusciamo a percepire, perché
è un suono continuo che corrisponde al nostro silenzio.
Come dice
Aristotele:
Vi
sono
alcuni che
ritengono
che il moto
di corpi così
grandi
debba
Fig. 5 Pitagora e gli intervalli musicali
espressi come rapporti numerici, in
un'illustrazione di un libro di Boezio.
necessariamente produrre un suono, dal momento
che questo accade anche con i corpi che ci
Fig. 6 Il cosmo secondo i pitagorici.
circondano, i quali né hanno mole pari a quelli né
si muovono con ugual velocità; e il sole e la luna, e poi le stelle, che sono in tal numero, e di tal grandezza,
e si muovono con un moto di tale velocità, è impossibile, dicono, che non producano un suono di intensità
straordinaria. Da queste premesse, e assumendo inoltre che le velocità, in virtù delle distanze fra i vari
astri, hanno rapporti di accordi consonanti, essi affermano che il suono prodotto dal moto circolare degli
astri è armonico. Ma parendo assurdo che di questo suono non s’abbia noi percezione, causa di ciò dicono
essere il fatto che questo suono ci accompagna già fin dalla nascita, per modo che esso non si lascia
distinguere nel contrasto col silenzio: solo contrapposti infatti suono e silenzio si lasciano distinguere.
Il rapporto fra numeri e musica, scoperto dai pitagorici, è un esempio del collegamento dei numeri con
l'armonia del cosmo.
Fig. 7 Pitagora che regge il cosmo.
Scrive Teone di Smirne:
Prendeva alcuni vasi tutti uguali e, mentre ne lasciava uno vuoto, riempiva il secondo d'acqua fino a
metà, poi li percuoteva entrambi e otteneva il rapporto di un'ottava. Quindi, lasciando ancora vuoto uno
dei vasi, riempiva l'altro per una quarta parte, e poi li percuoteva entrambi e otteneva il rapporto di
quarta. L'accordo di quinta l'otteneva riempiendo il vaso per la sua terza parte. Il rapporto tra il vuoto
di un vaso e quello dell'altro era dunque di 2 a 1 nell'accordo di ottava, di 3 a 2 nell'accordo di quinta e
di 4 a 3 nell'accordo di quarta.
I seguaci di Pitagora si dividevano in "acusmatici", ascoltatori, e
"matematici", gli unici che avevano diritto a conoscere gli
insegnamenti più profondi del maestro. Giamblico, il filosofo
neoplatonico che scrisse una Vita di Pitagora, afferma che chi aspirava
ad entrare nella comunità doveva osservare cinque anni di silenzio e
in questo periodo di tempo doveva già affidare alla comunità tutti i
suoi averi:
Fig. 8 Francobollo delle poste greche,
celebrativo di Pitagora.
Dopo cinque anni di silenzio, se risultava degno di essere iniziato alla
dottrina, diventava esoterico e poteva ascoltare e anche vedere
Pitagora dentro la tenda. Prima, fuori della tenda, aveva potuto
soltanto ascoltare le sue lezioni, senza mai vederlo.
Fatto eccezionale, anche le donne erano ammesse alle lezioni di
Pitagora. La vita dei pitagorici era per certi aspetti quasi monacale, in una comunione dei beni e
nell'osservanza di riti e regole molto rigorose che contribuivano a creare attorno alla scuola un alone di
rispetto e di mistero.
Ecco, nella descrizione di Giamblico, come i pitagorici chiudevano la loro giornata:
Nel tardo pomeriggio tornavano a passeggiare in gruppi di due o tre, per richiamare alla memoria le
cognizioni apprese e per esercitarsi negli studi liberali. Dopo il passeggio facevano un bagno e andavano
al banchetto comune. Al banchetto seguivano le libagioni e infine la lettura. Era consuetudine che
leggesse il più giovane e che il più anziano stabilisse quello che si doveva leggere e come.
3. Numeri: matematica, misticismo e magia
Per i pitagorici: "tutto è numero" ovvero ogni cosa può essere ridotta a una relazione numerica. E per i
pitagorici i numeri erano soltanto i numeri interi e questi erano il principio di tutte le cose. Essi
affermavano:
Tutte le cose che si conoscono hanno numero; senza questo nulla sarebbe possibile pensare o conoscere.
Essi applicarono la loro dottrina, fondata sui numeri, alla ricerca scientifica, suddivisa in quattro parti
essenziali: aritmetica, musica, geometria e astronomia. L'idea di una realtà fondata sulle interazioni fra gli
opposti, li portò a individuare dieci opposizioni fondamentali.
Fig. 9 Le dieci "opposizioni" dei pitagorici.
Queste opposizioni che riflettevano un assetto dualistico della realtà (... sicuramente "maschilista"),
venivano applicate alle loro speculazioni sui numeri e questi assumevano un valore simbolico, oltre la
matematica, magico e religioso. L'unità non era considerata propriamente un numero, 1 non era per i
pitagorici né pari né dispari, e questa sua ambivalenza rifletteva la concezione dualistica dell'universo, che
era rappresentato proprio dal numero 1. E questo era principio di tutti i numeri, come dice Dante (Paradiso,
XV, 57):
Raia da l'un, se si conosce, il cinque e il sei.
Per i pitagorici il numero 4 era il simbolo della giustizia, essendo il primo numero uguale al prodotto di
due numeri uguali, 2 x 2, e anche la giustizia doveva cercare di restituire "l'uguale all'uguale". Il numero 5
rappresentava il matrimonio, perché somma del primo numero pari (femminile), il 2, con il primo numero
dispari (maschile), il 3. E così via, ogni numero con un significato trascendentale.
Fig. 10 I pitagorici inventarono una singolare teoria, l' aritmogeometria, che collegava fra loro numeri e figure geometriche. Possiamo
immaginare che conducessero le loro analisi insieme agli allievi, sulle spiagge di Crotone, usando sassolini bianchi e neri per "costruire" i
numeri. Noi, se non abbiamo a disposizione una spiaggia ma soltanto un foglio di carta, useremo semplicemente dei punti. Dallo studio
di queste figure e dei numeri ad esse collegati si possono ricavare diverse proprietà aritmetiche e geometriche. Ancora oggi usiamo
l'espressione "tre al quadrato" o "due al cubo". Ma quanti sanno che queste espressioni derivano proprio dalla rappresentazione
geometrica dei due numeri: un quadrato di 3 per 3 punti o un cubo di 2 x 2 x 2 punti? I numeri "al triangolo" sono triangoli equilateri con
lati di 1, 2, 3, 4, 5, … punti. In tal modo il "triangolo" di 4 risulta 10: 1 + 2 + 3 + 4. I numeri "al pentagono" sono invece in forma di
pentagono. Abbiamo quindi 2 "al pentagono" uguale a 5 o 3 "al pentagono" uguale a 12. Con un procedimento analogo si possono
costruire numeri "all'esagono", "al tetraedro" e così via.
4. La Tetraktis e il Pentagramma
Il numero più importante per i pitagorici era il 10, il numero che rappresentava per loro
l'Universo. Dice Filolao:
Il 10 è responsabile di tutte le cose, fondamento e guida sia della vita divina e celeste, sia
di quella umana.
Il 10 è "quattro al triangolo" ed è inoltre la somma dei primi quattro numeri, 1 +
2 + 3 + 4 = 10, gli stessi numeri si ritrovano nei rapporti degli intervalli musicali,
come abbiamo appena visto. E il 10 rappresenta la somma di tutte le dimensioni:
un punto, che non ha dimensioni, 2 punti, che generano una linea a una
dimensione, 3 punti, che generano un triangolo in due dimensioni e 4 punti, che
generano un tetraedro nelle tre dimensioni. Il 10 era la sacra Tetraktis, simbolo
esoterico dei pitagorici. Riportiamo da Dantzig, la preghiera della Tetraktis che
veniva recitata dai pitagorici:
Benedici a noi, o numero divino, tu da cui derivano gli dei e gli uomini. O santa, santa
Tetrade, tu che contieni la radice, la sorgente dell'eterno flusso della creazione. Il numero
divino si inizia coll'unità pura e profonda, e raggiunge il quattro sacro; poi produce la
matrice di tutto, quella che tutto comprende, che tutto collega; il primo nato, quello che
giammai devia, che non affatica, il sacro dieci, che ha in sé la chiave di tutte le cose.
Anche Dante (Convivio 2, XIV, 3) aveva questa idea del dieci, come numero
perfetto:
Dal diece in su non si va se non esso diece alterando cogli altri nove e con sé
stesso.
Il 10 è anche considerato simbolo di pace e di fratellanza, infatti scambiandosi una stretta
di mano, due persone uniscono fra loro le dieci dita. E che il 10 sia sempre un numero
speciale lo conferma il fatto che i Comandamenti divini sono 10, o più semplicemente che
10 è il voto più bello che si può prendere a scuola.
Un'altra figura sacra ai pitagorici era il pentagramma, la stella a cinque punte,
racchiusa nel cerchio divino (fig. 11), segno di riconoscimento fra gli adepti.
Racconta Giamblico, a proposito del pentagramma:
Un pitagorico senza denaro si ammalò in un albergo. Sentendo la morte vicina invitò
l'oste, che l'aveva curato, ad esporre il pentagramma fuori dell'albergo. Molto più tardi
un altro pitagorico passando di là vide il simbolo, ne chiese spiegazione all'oste e lo
ricompensò generosamente per l'aiuto che aveva dato al suo compagno.
E il pentagramma è rimasto ancora oggi un simbolo sacro o magico, venduto persino come
amuleto. Qualcuno ritiene che il pentagramma con la punta in basso acquisti un valore
negativo, "diabolico", ma qui entriamo nel campo della superstizione e della stregoneria,
che non ci interessa.
Con questo intreccio di teoria e di magia dei numeri, di
simboli esoterici, di setta religiosa e di comunità
scientifica, la figura di Pitagora può essere vista come
filosofo e matematico, ma anche come profeta e mago
e la sua comunità come scuola, ma anche come setta
segreta.
Fig. 11 Il pentagramma
Sono i due aspetti di Pitagora - scrive Bertrand Russell - il
profeta religioso e il matematico puro. Da entrambi i punti
di vista ebbe una incommensurabile influenza, e i due aspetti
non si possono separare come potrebbe credere una mente
moderna.
L'influenza esercitata dai pitagorici risultò fondamentale per lo sviluppo della
filosofia greca classica e del pensiero medioevale europeo. Nel Rinascimento
alcune idee dei pitagorici, come la Tetraktis o le proporzioni armoniche vennero
applicate anche in campo artistico. Nel Seicento, Copernico dichiarava che il suo
sistema, con la Terra che gira attorno al Sole, era un sistema pitagorico e lo stesso
Galileo veniva considerato "pitagorico", poiché Pitagora era visto come il padre
delle scienze esatte.
5. Il teorema di Pitagora nell'antichità
Si racconta, ma è leggenda, che Pitagora abbia scoperto il suo teorema mentre stava
aspettando di essere ricevuto da Policrate. Seduto in un grande salone del palazzo del
tiranno di Samo, Pitagora si mise ad osservare le piastrelle quadrate del pavimento. Se
avesse tagliato in due una piastrella lungo una diagonale, avrebbe ottenuto due triangoli
rettangoli uguali. Inoltre l'area del quadrato costruito sulla diagonale di uno dei due
triangoli rettangoli risultava il doppio dell'area di una piastrella. Questo quadrato risultava
infatti composto da quattro mezze piastrelle, cioè da due piastrelle. Ma i quadrati costruiti
sugli altri lati del triangolo corrispondevano ognuno all'area di una piastrella.
Fig. 12 Dalle piastrelle del pavimento al teorema di Pitagora.
In altre parole il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati
costruiti sui due cateti. Questo risultava evidente nel caso della piastrella quadrata, cioè di
un triangolo rettangolo isoscele: Ma poteva essere vero, si chiese Pitagora, anche nel caso
generale, con cateti di lunghezza diversa?
Fig. 13 Dai triangoli rettangoli isosceli al caso generale.
Studiando meglio la figura ottenuta dall'osservazione delle piastrelle, Pitagora si accorse
che il quadrato formato da quattro piastrelle si poteva scomporre in quattro triangoli
rettangoli equivalenti e in un quadrato il cui lato era uguale alla lunghezza dell'ipotenusa
di uno dei triangoli. Non fu quindi difficile passare al caso generale di quattro triangoli
rettangoli qualsiasi, non più isosceli per i quali, come vedremo, vale ancora il teorema.
In realtà la storia del teorema è molto più complessa e
le sue origini, come abbiamo già detto, risalgono
almeno ad un migliaio di anni prima che Pitagora si
dedicasse allo studio dei triangoli rettangoli. Per
avviare la nostra indagine sul teorema partiamo dalla
formulazione che ne diede Euclide:
In ogni triangolo rettangolo il quadrato del lato
opposto all'angolo retto è uguale ai quadrati dei lati
che contengono l'angolo retto.
Se lo riscriviamo in termini più moderni abbiamo
l'enunciato riportato generalmente nei testi scolastici:
In ogni triangolo rettangolo il quadrato
dell'ipotenusa (oppure: l'area del quadrato costruito
sull'ipotenusa) è equivalente alla somma dei quadrati
dei due cateti (oppure: alla somma delle aree dei
quadrati costruiti sui due cateti).
Fig. 14 Il teorema di Pitagora.
Se c indica la lunghezza dell'ipotenusa e a e b quelle dei due cateti possiamo scrivere il
teorema in forma algebrica:
Il teorema di Pitagora era noto un tempo come "il ponte degli asini", il ponte che riusciva
a superare soltanto chi dimostrava di possedere sufficienti attitudini per il pensiero
astratto e per un metodo deduttivo da applicare a procedimenti matematici quali erano
quelli proposti dai pitagorici.
Ecco come Einstein ricorda il suo primo incontro con il teorema:
Avevo 12 anni quando un mio vecchio zio mi enunciò il teorema di Pitagora e dopo molti
sforzi riuscii a dimostrarlo. E’ stata un’esperienza meravigliosa scoprire come l’uomo sia
in grado di raggiungere un tale livello di certezza e di chiarezza nel puro pensiero. E sono
stati i Greci per primi ad indicarcene la possibilità, con la geometria.
Vediamo una delle
dimostrazioni
più
semplici, quella che
generalmente si trova
sui testi scolastici e che
riprende
il
ragionamento
che
Pitagora potrebbe aver
fatto osservando le
piastrelle quadrate nel
palazzo di Policrate.
Fig. 15 Una delle più semplici dimostrazioni di Pitagora, fondata sulle
equivalenze fra aree.
Dato
il
triangolo
rettangolo ABC (Fig. 16),
Fig. 16
di cateti a, b e ipotenusa c, costruiamo due quadrati equivalenti,
che abbiano come lato la somma dei due cateti, a + b (Fig. 15).
Scomponiamo il primo di questi quadrati nei due quadrati
costruiti sui cateti e nei quattro triangoli di figura, equivalenti al
triangolo dato. Scomponiamo poi il secondo quadrato nel
quadrato costruito sull'ipotenusa e negli stessi quattro triangoli.
Se ai due quadrati grandi togliamo i quattro triangoli uguali,
otteniamo due parti equivalenti, con la stessa area: i quadrati
costruiti sui cateti e il quadrato costruito sull'ipotenusa.
Attenzione però: la dimostrazione non è ancora
completa. E' necessario dimostrare ancora che le
parti più scure sono realmente i quadrati dei cateti
e dell'ipotenusa del triangolo dato. Per il primo
quadrato a sinistra (Fig. 15) questo è evidente, dal
modo in cui abbiamo eseguito la scomposizione,
cioè, come si dice,per costruzione. Per il secondo
quadrato a destra, sempre per costruzione,
possiamo dire che i suoi lati sono uguali
all'ipotenusa del triangolo. Resta da dimostrare
che i suoi angoli sono retti. Consideriamo
l'angolo a, che sommato agli altri due angoli
aventi lo stesso vertice forma un angolo piatto. Ma
anche la somma degli angoli interni di un
triangolo è uguale a un angolo piatto, e quindi
l'angolo a corrisponde al terzo angolo del
triangolo, che è retto. Allo stesso modo si
dimostra che anche gli altri angoli sono retti e
quindi che la figura è un quadrato.
Molte dimostrazioni si basano semplicemente
Fig. 17 Il teorema kou ku o "di Pitagora" in
sulla scomposizione di aree in parti uguali. Una di
un'illustrazione originale del Chou Pei
queste potrebbe provare che anche in Cina il
teorema "di Pitagora" era già noto almeno mille anni prima della nascita di Pitagora. E'
collegata a una figura, che si trova nel Chou Pei Suan Ching (Fig. 17) uno dei più antichi
testi cinesi di matematica, Il libro classico dello gnomone e delle orbite circolari del cielo,
scritto al tempo della dinastia Shang, 1500 - 1000 a. C..
Questa figura potrebbe essere una dimostrazione del teorema di Pitagora, chiamato dai
cinesi kou ku. Nel disegno di figura 17 si vede infatti un triangolo rettangolo di lati 3, 4 e 5
e un quadrato grande di lato 7 = 3 + 4.
Lo schema della figura 18 potrebbe aiutarci a ricostruire la dimostrazione originale che
purtroppo è andata perduta. Come possibile percorso della dimostrazione possiamo partire
dai quattro triangoli rettangoli, di cateti 3 e 4, collocati attorno al quadrato centrale di lato
1.
Fig. 18 Schema del disegno del Chou Pei (in alto a sinistra) e dimostrazioni del teorema di Pitagora di Liu Hui,
nella ricostruzione di D. B. Wagner, studioso danese dell’Antica Cina (in alto a sinistra) e in quella di Jöran Friberg,
un matematico svedese (in basso).
Se raddoppiamo i quattro triangoli, otteniamo il quadrato
grande di lato 7. L'area di questo quadrato grande è di 49
unità al quadrato. Per avere l'area del quadrato piccolo e
scuro, dobbiamo togliere l'area di quattro triangoli,
ognuno dei quali ha area 6 x 4, cioè 49 - 24 = 25. Il lato di
questo quadrato misura quindi 5 unità ed è l'ipotenusa del
triangolo
rettangolo
di
cateti
3
e
4.
Sempre in Cina Liu Hui, un grande matematico del terzo
secolo d. C., diede una dimostrazione del teorema "di
Pitagora" che è stata ricostruita da alcuni matematici
moderni seguendo le indicazioni che è stato possibile
ricuperare. Dice Liu Hui:
Siano il quadrato su kou [il cateto a] rosso e il quadrato su
ku [il cateto b]blu. Usate il principio della mutua
sottrazione e addizione di specie simili per inserire i resti, Fig. 19 Liu Hui, terzo secolo d.C..
in modo che non ci sia alcun cambiamento nell'area con l'aspetto di un quadrato
sull'ipotenusa.
Le dimostrazioni riportate in Fig. 18 sono graficamente molto belle e non hanno bisogno
di spiegazioni. Risultano infatti evidenti le parti equivalenti in cui sono state scomposte le
figure.
Anche dall'India arriva un enunciato del teorema di Pitagora che ci autorizza a pensare
come il teorema fosse già noto agli indiani in epoche precedenti alla nascita di Pitagora. Si
legge infatti nei Sulbasutra, i testi che contenevano le istruzioni per la costruzione degli
altari, riportati in forma scritta fra l'800 e il 600 a. C.:
La fune tesa per la lunghezza della diagonale di un rettangolo forma un'area pari alla
somma di quella formata dal lato verticale e da quello orizzontale.
Si parla ancora di funi e di problemi pratici. Ma la strada
è aperta verso la matematica astratta.
Dall'Arabia (Fig. 21) arriva invece la dimostrazione di
Thabit ibn Qurra Marwan al'Harrani (826 - 901):
I triangoli ABC, CEH, CEM, BGD, EGL, AFL sono tutti
equivalenti. Inoltre osserviamo che il poligono ABDEF
può essere scomposto in due modi diversi:
Fig. 20 Il teorema di Pitagora secondo
Sulbasutra.
e
Dall'uguaglianza delle due relazioni e dall'equivalenza dei triangoli indicati, ricaviamo:
Fig. 21 La dimostrazione araba di Thabit ibn Qurra
Pappo di Alessandria, nel quinto secolo d. C. propose una costruzione che è una
generalizzazione del teorema di Pitagora, valida anche nel caso in cui il triangolo non sia
rettangolo.
Fig. 22 La dimostrazione di Pappo.
Dato un triangolo qualsiasi ABC, costruiamo sui suoi cateti i parallelogrammi BDEC e
ACFG. Inoltre prendiamo il segmento IL uguale a HC e costruiamo il parallelogramma
ABNM con i lati AM e BN paralleli e uguali a IL. Poiché due parallelogrammi con la stessa
base e la stessa altezza sono equivalenti, abbiamo che BDEC è equivalente a BPHC e che
quest'ultimo è equivalente a BILN. Quindi BDEC è equivalente a BILN. In modo analogo
si dimostra che ACFG è equivalente a AMLI. La somma di BDEC e ACFG è dunque
equivalente a AMNB.
A questo punto possiamo rivedere, con l'aiuto di uno schema (Fig. 23), il collegamento tra
il teorema di Pitagora e la famosa tavoletta babilonese di cui parlavamo all'inizio del
capitolo.
Fig. 23 Lo schema della tavoletta babilonese, nella ricostruzione di O. Neugebauer, con il calcolo della diagonale di
un quadrato di lato 30. A destra nel sistema sessagesimale e a sinistra nel decimale.
Il primo numero sulla diagonale è 1;24,51,10, dove il punto e virgola separa la parte intera
dalla parte decimale ed è in notazione sessagesimale. Lo stesso numero nel sistema
decimale è:
che è un valore approssimato della radice di 2.
Se il lato del quadrato è 1, la diagonale è la radice quadrata di 1^2 più 1^2, cioè di 2. Se il
lato è 30, sarà naturalmente il prodotto di 30 per la radice quadrata di 2.
Ma la dimostrazione per eccellenza per i matematici è sicuramente quella di Euclide,
riportata nel primo libro degli Elementi, proposizione 47:
Nei triangoli retti il quadrato del lato che sottende l'angolo retto è uguale alla somma dei
quadrati dei lati che contengono l'angolo retto.
Questa dimostrazione fa riferimento a una figura (Fig. 24) che è stata battezzata, per la sua
forma particolare, mulino a vento, coda di pavone o sedia della sposa. Vediamola nei
termini usuali per uno studente, come la ritrova sul suo libro di geometria, nel capitolo
dedicato ai teoremi di Euclide.
Fig. 24 La sedia della sposa di Euclide.
Dato il triangolo rettangolo ABC, costruiamo i quadrati sui suoi lati e tracciamo CL
parallelo ad AD. I triangoli FAB e CAD sono uguali per il primo criterio di uguaglianza.
Hanno infatti AB = AD perché lati dello stesso quadrato ABDE, inoltre AF = AC, perché lati
dello stesso quadrato ACGF e gli angoli FAB e CAD sono uguali perché somma di un angolo
retto e di un angolo in comune, l'angolo CAB. Abbiamo perciò:
e
Inoltre i triangoli CAD e AMD hanno la stessa base AD e la stessa altezza AM, e sono quindi
equivalenti:
D'altra parte i triangoli FAB e FAC hanno anch'essi la stessa base AF e la stessa altezza AC,
quindi sono equivalenti:
Il rettangolo ADLM è perciò equivalente al quadrato ACGF.
Allo stesso modo dimostriamo che il quadrato BKHC
è equivalente al doppio del triangolo ABK e
quest'ultimo a sua volta è equivalente al doppio del
triangolo BCE, cioè al rettangolo BMLE:
Fig. 25 Euclide, 325-265 a.C. circa. Ritratto
da A, Thevet, Vite di uomini illustri, Parigi,
1584.
Se sommiamo le due equivalenze abbiamo:
Abbiamo così dimostrato che
La dimostrazione di Euclide, oltre a far disperare ancora oggi tanti studenti, fece arrabbiare
anche il celebre filosofo Arthur Schopenahuer, il quale accusò il grande matematico greco
di aver costruito una figura che porta a una interminabile catena di passaggi e che sembra
chiudersi su di noi come una “trappola per topi”. Schopenahuer presentò anche una sua
dimostrazione, magnificandone, con la presunzione che lo contraddistingueva, la chiarezza
e la semplicità. In realtà si tratta di una dimostrazione senza alcun valore, riguardante
soltanto il caso particolare del triangolo rettangolo isoscele. Proprio quello che era stato il
punto di partenza per Pitagora, lo studio delle piastrelle del palazzo di Policrate, ma
soltanto un punto di partenza, per arrivare alla dimostrazione generale del teorema.
6. Le mille dimostrazioni del teorema di Pitagora
Le dimostrazioni del celebre teorema non sono infinite, ma nel corso dei secoli ne sono state proposte
diverse centinaia, con molte varianti, e il loro numero continua a crescere grazie a quelle che ancora oggi
vengono scoperte da matematici professionisti o dilettanti, sempre affascinati da questo teorema. Se
andiamo a curiosare fra le tante dimostrazioni, ne troviamo alcune veramente curiose.
Sicuramente Schopenahuer più della dimostrazione di Euclide, avrebbe apprezzato quella proposta nel
1873 da Henry Perigal (Fig. 27), un agente di cambio inglese con la passione per la matematica. Egli divide
il quadrato costruito sul cateto maggiore in quattro parti, con due segmenti passanti per il centro del
quadrato stesso, uno dei quali parallelo e l'altro perpendicolare all'ipotenusa BC, e ricompone poi i
quattro pezzi, insieme al quadrato costruito sull’altro cateto, nel quadrato dell’ipotenusa. Si tratta
naturalmente di dimostrare l'equivalenza delle parti in cui sono stati divisi i quadrati dei cateti con quelle
ricomposte sul quadrato dell'ipotenusa .
Fig. 27 La dimostrazione dell'agente di cambio Perigal.
Sempre con la scomposizione in parti equivalenti, sono riportate nelle figure delle due pagine seguenti
alcune altre costruzioni e dimostrazioni del teorema di Pitagora. Sono state evidenziate soltanto le
scomposizioni in parti equivalenti, lasciando al lettore il compito delle dimostrazioni.
Fig. 28 Dimostrazione di Tempelhoff, 1769, riportata da I. Ghersi in Matematica dilettevole e curiosa. Dato il triangolo rettangolo ABC,
si costruiscano i quadrati sui suoi tre lati e il triangolo DLE come indicato in figura. Si traccino poi i segmenti HG, IF e CL. Si può
dimostrare che i quadrilateri FGHI, ABFI, ADLC e BCLE sono equivalenti. L'esagono ABFGHI è quindi equivalente all'esagono ADLEBC.
Ma se togliamo ai due esagoni il triangolo in comune ABC e i triangoli equivalenti CGH e DLE, quanto rimane è ancora equivalente:
AB²=AC²+BC².
Fig. 29 Molto semplice e bella è anche la costruzione di Nassir - ed - Din che si trova nell'Edizione araba degli Elementi, Roma, 1594. In
figura abbiamo ACMN equivalente sia ad AC² che a ADPO. E' quindi ADPO è equivalente ad AC². In modo analogo si vede che BOPE è
equivalente a BC². Ricaviamo perciò:
AB²= AC²+ BC²
Resta da dimostrare, prima di tutto, che il segmento MP passa per i punti C ed O.
Fig. 30 Una costruzione del 1778 di Ozanam, riportata da I. Ghersi in Matematica dilettevole e curiosa. Molto semplice ed elegante, da
provare con "carta e forbici". Resta poi sempre la dimostrazione dell'equivalenza delle varie parti.
Fig. 31 Una scomposizione simile alla precedente. I due quadrati sui cateti sono stati divisi prima con una diagonale e successivamente
con due segmenti paralleli all'ipotenusa, uscenti dai vertici dell'altra diagonale. Le otto parti si ricompongono nel quadrato
sull'ipotenusa.
Fig. 32 Un'altra costruzione che mette in evidenza il teorema di Pitagora. A sinistra, un quadrato avente per lato la differenza dei due
cateti di un triangolo rettangolo e quattro triangoli rettangoli equivalenti, di cateti a e b e di ipotenusa c, si compongono nei quadrati dei
due cateti. A destra le stesse parti si compongono nel quadrato dell'ipotenusa.
Nel Giardino di Archimede, Un museo per la matematica, alle pagine web dedicate a Pitagora, si trova
una dimostrazione, simile alla precedente, ma in poesia, trovata pare, nel secolo scorso, da un astronomo
dell'osservatorio di Greenwich, G. B. Airy.
Fig. 33 La dimostrazione "poetica" di G. B. Airy.
Se il lettore osserva la fig. 33, saprà ricavarne immediatamente la dimostrazione: i due triangoli gialli con
la parte bianca formano il quadrato dell'ipotenusa, mentre la stessa parte bianca con i due triangoli verdi,
equivalenti ai precedenti, formano i quadrati dei cateti, com'è facilmente verificabile. Airy presenta
poeticamente la figura in questo modo:
I am, as you can see,
a² + b² - ab
When two triangles on me stand,
Square of hypothenuse is plann'd
But if I stand on them instead
The squares of both sides are read.
Tentiamone una traduzione:
Come potete veder, son qui:
a² + b² - ab
Se due triangoli sono sopra di me
Il quadrato dell'ipotenusa c'è
E se questi di sotto invece stanno
I quadrati dei cateti si hanno.
Vediamo ancora la dimostrazione trovata nel 1876 da James A. Garfield, ventesimo presidente degli Stati
Uniti. Antischiavista, eroe della guerra civile, Garfield venne eletto presidente nel 1880 e avviò subito una
campagna contro la corruzione politica, procurandosi per questo molti nemici. Pochi mesi dopo la sua
elezione, venne ferito con alcuni colpi di pistola.
Fig. 34 James Abram Garfield, 1831 - 1881.
A. G. Bell, l'inventore del telefono, tentò di individuare la posizione della pallottola rimasta nel corpo di
Garfield con un metal detector di sua invenzione. Ma non si accorse che il letto sul quale giaceva il
presidente aveva una rete metallica che disturbava l'uso del suo apparecchio. Il suo intervento fu quindi
inutile e il Presidente morì dopo alcuni giorni, anche per colpa dei medici che lo avevano visitato. I grandi
medici chiamati a consulto erano riusciti soltanto ad aggravare le sue condizioni per le scarse condizioni
igeniche in cui avevano operato.
Garfield trovò una dimostrazione inedita del teorema insieme ad alcuni suoi colleghi del Congresso, in
un "momento di passatempo matematico". "Pensiamo che su questa dimostrazione - disse - si possano
trovare d'accordo tutti i deputati, indipendentemente dalle loro idee politiche".
La dimostrazione di Garfield, molto bella, si fonda sul calcolo dell’area del trapezio. In questo caso non
dobbiamo costruire alcun quadrato.
Fig. 35 La dimostrazione di James A. Garfield, trovata nel 1876.
Sull’ipotenusa del triangolo rettangolo ABC viene costruito il triangolo rettangolo isoscele CBE. Si prolunga
la retta AC fino ad incontrare in D la perpendicolare tracciata da E.
Il triangolo ABC è uguale al triangolo DCE, perciò: AB = DC e AC = DE.
Sia l'altezza che la somma delle basi sono x + y e quindi l’area del trapezio ABDE è:
Ma l’area dello stesso trapezio è anche uguale alla somma delle aree dei tre triangoli ABC, BCE e CDE:
Abbiamo quindi:
Se si semplifica, si ottiene la relazione del teorema di Pitagora:
x2 + y2 = z2
7. Non solo triangoli
Il teorema di Pitagora continua ad essere valido anche se si sostituiscono i triangoli rettangoli con altre
figure, ad esempio, triangoli scaleni, pentagoni, esagoni o poligoni irregolari, purché siano sempre figure
simili fra loro, conservino cioè la stessa forma e differiscano soltanto per le dimensioni.
Fig. 36 Pitagora con i pentagoni.
Fig. 37 Pitagora con i semicerchi.
Ad esempio, per i pentagoni costruiti sui lati del triangolo rettangolo di figura 36, l'area del pentagono
sull'ipotenusa è equivalente alla somma delle aree dei pentagoni sui cateti. In figura 37, per i tre semicerchi
costruiti sui lati del triangolo rettangolo, l'area del semicerchio sull'ipotenusa è equivalente alla somma dei
semicerchi sui cateti.
Da quest'ultima costruzione si arriva a un risultato molto interessante. Se ribaltiamo il semicerchio
sull'ipotenusa (fig. 38) vale sempre naturalmente la relazione precedente: il semicerchio sull'ipotenusa
(ribaltato) è equivalente alla somma dei semicerchi sui cateti. Togliamo poi le parti più scure, sia al
semicerchio sull'ipotenusa che ai due semicerchi sui cateti. Rimarranno rispettivamente il triangolo e le
due parti più chiare la cui somma risulta equivalente all'area del triangolo, perché differenze di aree uguali.
Le due figure chiare a forma di luna, vengono chiamate lunule, piccole lune, dal latino lunulae. Nel caso di
un triangolo rettangolo isoscele (fig. 39), una lunula è quindi equivalente alla metà del triangolo. In questo
modo risulta che una figura rettilinea, il triangolo rettangolo, ha la stessa area di una figura curvilinea, la
lunula. Il primo ad aver dato questa dimostrazione pare che sia stato Ippocrate di Chio, nel quarto secolo
a. C.
Fig. 38 Le lunule di Ippocrate.
Fig. 39 Il caso del triangolo rettangolo isoscele.
8. Terne pitagoriche
L'altra faccia del teorema di Pitagora. Finora abbiamo parlato dell'aspetto
geometrico del teorema, di triangoli rettangoli. Vediamone ora l'aspetto
aritmetico, cioè le particolari terne numeriche, chiamate terne pitagoriche,
collegate al teorema stesso. Già sappiamo che in un triangolo rettangolo di
cateti a, b e di ipotenusa c si ha: a² + b² = c². Esistono infinite terne con
numeri interi che soddisfano a questa relazione. Una di queste è 3, 4 e 5.
Infatti con questi tre numeri si ha: 3² + 4² = 5².
Altre terne sono 5, 12 e 13, 7, 24 e 25, 8, 15 e 17, 20, 21 e 29. Per costruire Fig. 40 Il triangolo rettangolo 3, 4 e 5.
un triangolo rettangolo è sufficiente costruire un triangolo con le misure
dei lati corrispondenti ai numeri di una delle terne pitagoriche, ad esempio di 3, 4 e 5 unità. Lo possiamo
verificare praticamente con una scatola di fiammiferi, costruendo un triangolo che abbia come lunghezza
dei lati 3, 4 e 5 fiammiferi. Il triangolo ottenuto avrà sicuramente un angolo retto.
C'è un'altra famosa tavoletta del periodo
paleobabilonese, nota come Plimpton 322,
che dimostra come il problema aritmetico,
collegato a quello geometrico del teorema di
Pitagora, fosse già noto ben prima dei greci.
Questa
tavoletta
(fig.
41)
era
originariamente molto più grande, ma la
parte conservata permette ancora di
interpretare correttamente il significato
delle colonne di numeri che presenta.
Si tratta infatti di numeri collegati fra loro
dalla relazione del teorema, cioè numeri per
i quali il quadrato del numero più grande è
uguale alla somma dei quadrati degli altri
due numeri. A confermarci questa
interpretazione sono anche i titoli di
ciascuna colonna, in particolare della
seconda e della terza: "numero risolvente
Fig. 41 La tavoletta babilonese, Plimpton 322.
della larghezza" e "numero risolvente della
diagonale". I numeri di queste terne corrispondono, naturalmente nel sistema sessagesimale, alle
lunghezze dell'ipotenusa e di un cateto di triangoli rettangoli.
A questo punto, sembrerebbe logico supporre che il collegamento fra terne pitagoriche e triangoli
rettangoli, cioè fra il problema aritmetico e il corrispondente problema geometrico, fosse già noto
nell'antichità, ai babilonesi. In realtà la loro geometria era di tipo pratico, non esisteva un pensiero
geometrico indipendente dalle più semplici e immediate applicazioni. Scrive in proposito O. Neugebauer
nel suo prezioso saggio, Le scienze esatte nell’Antichità, in cui presenta un approfondito studio della
tavoletta Plimpton 322:
Soltanto in base alla nostra educazione, modellata sull’idea che i Greci avevano della Matematica, siamo
portati a pensare immediatamente alla possibilità di una rappresentazione geometrica di rapporti
aritmetici o algebrici.
Il collegamento fra il problema aritmetico e il corrispondente problema geometrico,
cioè fra e terne pitagoriche e triangolo rettangolo non fu probabilmente così
immediato. E' difficile pensare che il teorema di Pitagora abbia potuto avere origine
dalla conoscenza della terna pitagorica 3, 4 e 5.
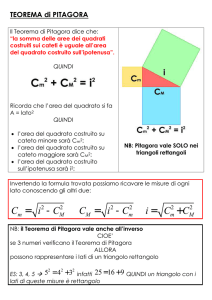
Una precisa dimostrazione di questo teorema, che possiamo definire l'inverso del
Fig. 42
teorema di Pitagora si troverà soltanto in Euclide. Nel primo libro dei suoi Elementi,
subito dopo il teorema di Pitagora, proposizione 47, si trova, alla proposizione 48, il teorema inverso:
Se in un triangolo il quadrato di un lato è uguale alla somma dei quadrati dei due lati rimanenti, allora
l'angolo contenuto dai due lati rimanenti è retto.
Noi sappiamo che in un triangolo rettangolo di cateti a, b e di ipotenusa c si ha a² + b² = c². Ma vale anche
l'inverso: se a, b e c sono i lati di un triangolo e vale la relazione a² + b² = c², allora il triangolo è
rettangolo, a e b sono i cateti e c l'ipotenusa del triangolo. La dimostrazione di Euclide è molto semplice.
Se il triangolo dato ABC non fosse rettangolo (fig. 41), costruiamo allora un triangolo rettangolo ACD con
AD perpendicolare ad AC e uguale ad AB, di cateti a e b e di ipotenusa d. Applichiamo il teorema di Pitagora
al triangolo rettangolo ACD e abbiamo
a² + b² = d²
ma per ipotesi abbiamo anche
a² + b² = c².
Ne consegue che c² = d² e quindi c = d. I due triangoli sono uguali
per il terzo criterio di uguaglianza e di conseguenza l'angolo BAC
dev'essere retto.
Ma ritorniamo alle terne pitagoriche. Lo studio delle terne babilonesi
sembrerebbe confermare la conoscenza da parte loro delle formule
fondamentali per la costruzione delle terne stesse. Sono formule che
Fig. 43 L'inverso di Pitagora.
tradizionalmente vengono attribuite a Diofanto, un matematico
greco vissuto nel terzo secolo dopo Cristo, autore di un'opera famosa, l'Arithmetica, in cui sono raccolti 189
problemi risolti applicando diversi metodi che rivelano la sua straordinaria abilità. Della sua vita non
sappiamo nulla, ci è rimasto soltanto un problema di un antico libro greco del quinto secolo d. C.:
Dio gli concesse di rimanere fanciullo per un sesto della sua vita, e trascorso un altro dodicesimo, Egli gli
coperse le guance di peluria. Dopo un settimo della sua vita Egli gli accese la fiaccola del matrimonio e
cinque anni dopo il matrimonio gli concesse un figlio che morì dopo aver raggiunto la metà della vita di
suo padre. Dopo aver consolato il proprio dolore con la scienza dei numeri per quattro anni, pose termine
alla sua vita.
Quanti anni aveva Diofanto quando morì? La risposta alla fine del capitolo.
Le formule delle terne pitagoriche, di cui si trova traccia già nella matematica babilonese e che furono
riprese da Diofanto sono molto semplici. Dati due numeri interi qualsiasi m e n, con m > n, si ha:
a = m² - n²
b = 2mn
c = m² + n²
E' facile verificare che a² + b² = c² , infatti:
a² + b² = (m² - n²)² + (2mn)² = m^4 + n^4 - 2m²n² + 4 m²n² = m^4 + n^4 + 2m²n² = (m² + n² )² = c²
Le tre formule ci danno quindi tutte le possibili terne pitagoriche a, b e c, tali che a² + b² = c² .
Si osservi che moltiplicando a, b e c per uno stesso numero, si ottiene ancora una terna pitagorica, infatti
si ottiene ancora un triangolo rettangolo, simile al precedente. Ad esempio, dalla terna 3, 4 e 5 abbiamo
3 x 2, 4 x 2 e 5 x 2 = 6, 8 e 10
3 x 6, 4 x 6 e 5 x 6 = 18, 24 e 30
e queste sono ancora terne pitagoriche. Infatti
6² + 8² = 10²
18² + 24² = 30²
Possiamo limitare la nostra ricerca a quelle che si chiamano terne primitive, cioè con a e b primi fra loro,
partendo da valori di m e di n primi fra loro. Tutte le altre terne saranno semplicemente multiple di quelle
trovate.
Ci sono due casi particolari interessanti. Se n = m - 1 si ha b = c - 1 e quindi b e c risultano, in questo caso,
numeri consecutivi, la differenza fra c e b sarà sempre uguale a 1. Ad esempio, con m = 2 e n = 1 la terna
corrispondente è 3, 4 e 5. Con m = 3 e n = 2 si ha la terna 5, 12 e 13. Provi il lettore a dimostrare questa
proprietà delle terne.
Se invece si prende per m un valore qualsiasi e n costante, uguale a 1, si otterranno delle terne pitagoriche
per le quali la differenza fra l'ipotenusa e il cateto maggiore sarà sempre uguale a 2. Ad esempio
con muguale a 6 e n uguale a 1 si ha la terna 12, 35 e 37.
Osserviamo ancora che, in generale, la differenza fra il numero più grande e quello più piccolo della terna
è uguale al quadrato della differenza fra i due numeri generatori. Ad esempio, con m = 5 n = 2 abbiamo la
terna 20, 21 e 29. La differenza fra i due numeri generatori, m e n, è 3 e la differenza fra i due numeri è 29
- 20 = 9.
La somma fra il numero più grande della terna e quello più piccolo è invece uguale al quadrato della somma
dei due numeri generatori. Nel nostro esempio precedente abbiamo m + n = 5 + 2 = 7 e la somma dei due
numeri è 29 + 20 = 49.
9. Oltre le terne pitagoriche.
E' logico estendere le terne pitagoriche alla terza dimensione. Per esempio, alla diagonale di un
parallelepipedo le cui dimensioni siano a, b e c. In questo caso la diagonale d del parallelepipedo è d² = a²
+ b² + c². Dalle terne passiamo così alle quaterne pitagoriche. Abbiamo, ad esempio, la quaterna 3, 4, 12
e 13 per la quale si ha 3² + 4² + 12² = 13²
Fig. 44 Le quaterne pitagoriche, nelle tre dimensioni.
Proviamo ora a passare dalle terne alle cinquine pitagoriche, che definiamo come cinquine di numeri tali
che la somma dei primi tre sia uguale alla somma degli ultimi due. Seguiamo per questo un lavoro fatto (...
qualche anno fa) da una ragazzina di terza media, Luisa Lanfranco.
Dobbiamo trovare una cinquina di numeri a, b, c, d ed e tali che:
a² + b² + c² = d² + e²
Per risolvere questo problema e trovare le nuove formule, partiamo dalle formule di Diofanto:
a = m² + n²
b = m² - n²
c = 2mn
dove m e n sono sempre due numeri qualsiasi, con m maggiore di n, e aggiungiamo due nuove formule:
d=c+b
e=c-b
I cinque numeri calcolati in questo
Ad esempio, prendiamo m = 5 e n = 4.
modo
formano
proprio
una
cinquina
pitagorica.
a = 5² + 4² = 25 + 16 = 41
b = 5² - 4² = 25 - 16 = 9
c = 2 x 5 x 4 = 40
d = 40 + 9 = 49
e = 40 - 9 = 31
La cinquina 41, 9, 40, 49 e 31 è "pitagorica", infatti:
41² + 9² + 40² = 49² + 31² cioè:
1 681 + 81 + 1 600 = 2 401 + 961 = 3 362
A questo punto abbiamo soltanto accennato alla possibilità di avviare una curiosa e ricca ricerca, oltre le
terne pitagoriche. Saprebbe, ad esempio, il lettore trovare le settuple pitagoriche? Dovrebbe cioè scoprire
la regola che permette di costruire la settupla a, b, c, d, e, f e g tale che si abbia:
a² + b² + c² + d² + e² = f² + g²
dati due numeri m e n qualsiasi, con m maggiore di n.
La risposta alla fine di questi appunti.
10. Il teorema di Fermat
Dalle terne pitagoriche è naturale passare allo studio delle terne di numeri di potenza superiore al due.
Come abbiamo visto, un numero quadrato, come ad esempio 25, può essere spezzato nella somma di due
quadrati, in questo caso 9 e 16. Ci chiediamo: è possibile spezzare un cubo in due cubi oppure una quarta
potenza nella somma di due numeri che siano entrambi quarte potenze? Ad esempio, 27, il cubo di 3, può
essere diviso nella somma di due cubi? E' possibile trovare terne di numeri interi che soddisfino alla
relazione x^3 + y^3 = z^3 e, in generale
x^n + y^n = z^n ?
Il protagonista di questa ricerca è stato Pierre de Fermat (1601 - 1665), di professione avvocato, con la
passione della matematica.
E' stato definito il "principe dei dilettanti", per i risultati straordinari che raggiunse non soltanto nella
teoria dei numeri, ma anche in altri campi, come la geometria analitica e il calcolo infinitesimale. Fermat
affermò che la scomposizione non è possibile né con i cubi né con qualsiasi altro numero di potenza
superiore al due. Sul margine di un libro che stava leggendo, l'Arithmetica di Diofanto, scrisse:
Cubem autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in
infinitum ultra quadratum potestatem in duos ejusdem nominis fas est dividere: cujus rei
demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.
Non è invece possibile dividere un cubo in due cubi o un
quadrato - quadrato in due quadrato - quadrati e in genere
nessuna potenza superiore al due in due potenze dello stesso
ordine. Di questo ho trovato una splendida dimostrazione, ma la
ristrettezza del margine di questo libro non la può contenere.
In realtà la sua dimostrazione non venne mai trovata e non siamo
nemmeno sicuri che fosse realmente arrivato a scoprirla, ma
l'affermazione di Fermat, data la sua autorevolezza, venne presa
in seria considerazione da tutti i matematici. Molti si
impegnarono nella ricerca di una dimostrazione di quello che
venne battezzato l'"Ultimo teorema di Fermat", o meglio, non
"teorema" ma "congettura", visto che della dimostrazione non
c'era traccia.
Fra le carte
Fig. 45 Pierre de Fermat (1601 - 1665) di Fermat
venne
trovata la dimostrazione dell'impossibilità di soluzioni
intere di x^n + y^n = z^n per n = 4 e, nel Settecento,
Eulero, il celebre matematico svizzero, dimostrò
l'impossibilità di soluzioni intere per n = 3.
Nell'Ottocento altri matematici, come Legendre e
Lejeune - Dirichlet, dimostrarono autonomamente il
caso n = 5. Ma la soluzione generale del problema
sembrava impossibile. Con l'avvento del computer si
iniziò a calcolare pedestremente le terne per valori
sempre più alti di n. Negli anni Ottanta del secolo
scorso si arrivò a verificare tutti i valori di n fino a
25.000 e in tempi ancora più vicini ai nostri fino
a n uguale a 4 milioni. Ma la verifica al computer era
inutile, senza una dimostrazione generale non si
poteva essere sicuri che il teorema fosse valido per un
qualsiasi n. E il fascino per il problema posto da
Fermat restava inalterato.
Si racconta che, all’inizio del Novecento, un ricco
Fig. 46 L'Arithmetica di Diofanto in una edizione
industriale tedesco, Paul Wolfskehl, innamorato di
francese del 1670, con l'annotazione di Fermat.
una donna bellissima che lo aveva respinto, avesse
deciso di suicidarsi. Ma qualche giorno prima di attuare il suo folle gesto, aveva iniziato a leggere un libro
di matematica che parlava del grande teorema di Fermat. Wolfskehl restò catturato dal teorema e
pensando di aver trovato la via della dimostrazione, si buttò a capofitto nello studio della teoria dei
numeri, dimenticando la sua bella e i suoi tragici propositi. Anche se non riuscì nella sua impresa
matematica, grato a Fermat e al teorema che gli aveva salvato la vita, decise di istituire un premio
destinato a chi fosse riuscito a trovare la dimostrazione. Un premio consistente, pari a circa tre miliardi di
lire attuali.
Secondo un’altra versione, meno romantica, Wolfskehl, scapolo impenitente, all’età di 47 anni venne
obbligato dalla sua famiglia a sposare una donna che non amava e che lo rese infelice. Per vendicarsi di lei,
decise di lasciare per testamento le sue fortune all’uomo che fosse riuscito a dimostrare il teorema di
Fermat, doveroso omaggio alla teoria dei numeri, unica sua consolazione nell’inferno domestico.
Il premio venne annunciato nel 1908 e soltanto in quell’anno
vennero presentate ben 621 dimostrazioni, tutte sbagliate. Nel
1995, finalmente il premio è stato ufficialmente consegnato ad
Andrew Wiles, il matematico inglese che è riuscito nella storica
impresa.
L’Accademia delle Scienze di Gottinga, responsabile del premio e
del controllo delle dimostrazioni, dopo due anni di attente e
minuziose verifiche del risultato raggiunto da Wiles ha sciolto ogni
riserva, decretando la validità della sua dimostrazione.
La svalutazione ha ridotto il premio a trentamila marchi, ma "è
molto più importante di un premio Nobel - ha sottolineato Heinz
Fig. 47 Andrew Wiles, il matematico Wagner, il presidente dell’Accademia, durante la cerimonia di
che ha risolto il teorema di Fermat. premiazione - perché i Nobel vengono assegnati ogni anno, mentre
per il Premio Wolfskehl si è dovuto attendere novant'anni". E finalmente Fermat può riposare in pace.
Quello che è stato il tormento dei matematici per 260 anni, dal momento in cui venne enunciato nel 1637,
noto come l’Ultimo Teorema di Fermat, è risolto, anche se sono in molti a dubitare che Fermat avesse
realmente trovato la dimostrazione. Wiles, nato nel 1950, scoprì questo teorema quando aveva soltanto
dieci anni, leggendo un libro preso in prestito alla biblioteca.
"Sembrava così semplice - ricorda - e tuttavia i grandi matematici del passato non erano riusciti a
risolverlo. Era un problema che io, un ragazzo di dieci anni, potevo perfettamente capire. Mi resi conto in
quel momento che non lo avrei più abbandonato. Dovevo risolverlo. E all’inizio lo affrontai pensando che
Fermat, ai suoi tempi, non doveva certo conoscere più matematica di quella che conoscevo io".
Dopo molti tentativi, solo nel 1986, quand’era già docente alla Princeton University, Wiles capì di essere
sulla strada giusta. Decise allora di abbandonare ogni lavoro che non fosse collegato all’Ultimo Teorema.
Per sette anni visse come un recluso, senza far parola ad alcuno della sua ricerca.
Dobbiamo dire francamente che non è questo il modo di
lavorare che apprezziamo in un matematico. Riteniamo che
ci debba sempre essere collaborazione, scambio di
informazioni, ricerche comuni invece di egoistiche chiusure,
anche se possiamo comprendere l'ambizione di Wiles, il suo
desiderio di raggiungere fama e successo attraverso la
soluzione del problema.
"Il teorema di Fermat - ricorda ancora Wiles - era l’unico
mio pensiero. Il primo quando mi svegliavo al mattino,
quello che avevo in mente per tutta la giornata e l’ultimo, al
momento di andare a dormire". Unica distrazione i rari
momenti dedicati alla moglie e ai tre figli. "Ogni volta che
ricorda la sua avventura, quella che definisce l’ossessione
della sua vita - dice Simon Singh, autore di un libro di
Fig. 48 Andrew Wiles ad una presentazione
successo, L'ultimo teorema di Fermat - la sua voce si
della sua dimostrazione.
affievolisce, diventa esitante, tradendo l’emozione che
ancora prova a parlare del problema". Alla fine, convinto di
aver trovato la soluzione, nel 1993, decise di renderla pubblica. Televisioni e giornali lo presentarono come
"il più grande matematico del secolo", il genio che aveva vinto la grande sfida.
Ma la sua odissea matematica non era ancora finita. Quando pensava ormai di potersi concedere un
meritato riposo e di godersi il suo momento di gloria, due mesi dopo l’annuncio, venne scoperto un errore
nella sua dimostrazione. "Un errore così astratto che non posso descriverlo in modo semplice. Anche se
dovessi spiegarlo a un matematico - dice Wiles - dovrei chiedergli di avere la pazienza di studiare per due o
tre mesi la parte della mia dimostrazione in cui compare l’errore".
Possiamo immaginare lo stato d’animo di Wiles, costretto ad ammettere pubblicamente l’errore. Superata
la crisi e sempre convinto della correttezza dei suoi ragionamenti, riprese il suo manoscritto e per due
anni, dimostrando una caparbietà e una forza d'animo eccezionali, si ributtò a capofitto sul suo lavoro per
cercare di correggere l’errore. Alla fine ripresentò la sua dimostrazione che, con il premio Wolfskehl, ha
ricevuto la conferma definitiva. Questa dimostrazione è una relazione di duecento pagine ed è
naturalmente escluso che possa essere quella originale di Fermat. Sono molti i matematici, in particolare i
dilettanti, che continuano la ricerca per scoprire la prova più semplice che Fermat poteva avere in mente:
la storia dell’Ultimo Teorema non è ancora finita.