TEOREMA DI PITAGORA
a
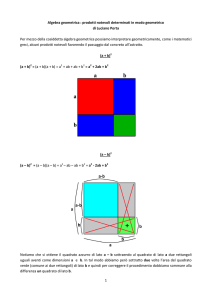
“IN UN TRIANGOLO RETTANGOLO IL QUADRATO
c
DELL’IPOTENUSA È UGUALE ALLA SOMMA DEI
QUADRATI DEI CATETI”
b
c2 = a 2 + b2
Si possono dare molte diverse dimostrazioni del teorema di Pitagora, vediamone una.
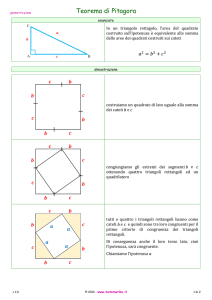
Costruiamo il quadrato di lato a+b come nella figura seguente:
a
b
a
c
b
c
c
c
a
b
b
a
• I quattro triangoli rettangoli colorati sono uguali al triangolo di partenza perché hanno l’angolo
retto e i due cateti a e b uguali. Ne consegue che hanno anche la stessa ipotenusa c e gli stessi
angoli acuti, la cui somma è 90°.
• Allora il quadrilatero bianco è un quadrato, avendo 4 lati uguali e 4 angoli di 90°
• L’area del quadrato bianco è S bianco = c 2
• L’area dei quattro triangoli rettangoli colorati è: S colorata = 4 S triangolo = 4 ⋅
• L’area del quadrato grande è: S grande = (a + b )2 = a 2 + 2ab + b 2
a ⋅b
= 2ab
2
• Tra queste tre aree vale la ovvia relazione: S bianco = S grande − S colorata
Ricaviamo quindi la seguente espressione per il quadrato dell’ipotenusa:
(
)
c 2 = S bianco = S grande − S colorata = a 2 + 2ab + b 2 − 2ab = a 2 + 2ab + b 2 − 2ab = a 2 + b 2
quindi abbiamo dimostrato che
c2 = a 2 + b2
e la dimostrazione è finita.
…………………………………………………………………………………………………………
Il Teorema di Pitagora può essere dimostrato in molti modi (chi è curioso cerchi in Rete e vedrà),
questo che fa uso delle aree e di un po’ di algebra è uno dei più semplici.