http://www.ripmat.it/piano.html
Primo teorema di Euclide
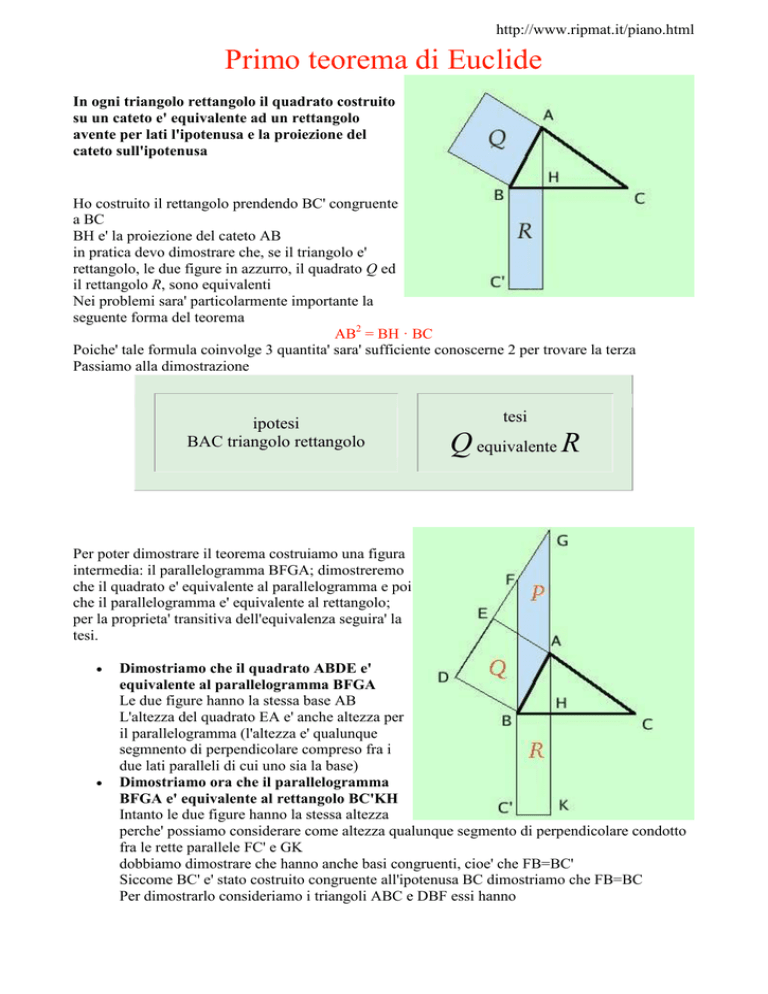
In ogni triangolo rettangolo il quadrato costruito
su un cateto e' equivalente ad un rettangolo
avente per lati l'ipotenusa e la proiezione del
cateto sull'ipotenusa
Ho costruito il rettangolo prendendo BC' congruente
a BC
BH e' la proiezione del cateto AB
in pratica devo dimostrare che, se il triangolo e'
rettangolo, le due figure in azzurro, il quadrato Q ed
il rettangolo R, sono equivalenti
Nei problemi sara' particolarmente importante la
seguente forma del teorema
AB2 = BH · BC
Poiche' tale formula coinvolge 3 quantita' sara' sufficiente conoscerne 2 per trovare la terza
Passiamo alla dimostrazione
ipotesi
BAC triangolo rettangolo
tesi
Q equivalente R
Per poter dimostrare il teorema costruiamo una figura
intermedia: il parallelogramma BFGA; dimostreremo
che il quadrato e' equivalente al parallelogramma e poi
che il parallelogramma e' equivalente al rettangolo;
per la proprieta' transitiva dell'equivalenza seguira' la
tesi.
•
•
Dimostriamo che il quadrato ABDE e'
equivalente al parallelogramma BFGA
Le due figure hanno la stessa base AB
L'altezza del quadrato EA e' anche altezza per
il parallelogramma (l'altezza e' qualunque
segmnento di perpendicolare compreso fra i
due lati paralleli di cui uno sia la base)
Dimostriamo ora che il parallelogramma
BFGA e' equivalente al rettangolo BC'KH
Intanto le due figure hanno la stessa altezza
perche' possiamo considerare come altezza qualunque segmento di perpendicolare condotto
fra le rette parallele FC' e GK
dobbiamo dimostrare che hanno anche basi congruenti, cioe' che FB=BC'
Siccome BC' e' stato costruito congruente all'ipotenusa BC dimostriamo che FB=BC
Per dimostrarlo consideriamo i triangoli ABC e DBF essi hanno
http://www.ripmat.it/piano.html
BÂC = BD̂F perche' entrambi angoli retti: uno per ipotesi e l'altro perche' angolo di
un quadrato
DB = AB perche' lati di un quadrato
DB̂F = AB̂C perche' complementari dello stesso angolo FB̂A
cioe' se li sommo con l'angolo FB̂A ottengo da entrambi un angolo retto
quindi i due triangoli sono congruenti per il secondo criterio di congruenza ed in particolare
avremo che BF=BC
Il parallelogramma ed il rettangolo hanno quindi anche congruente la base e pertanto sono
equivalenti
Allora il quadrato Q e' equivalente al parallelogramma P e quest'ultimo e' equivalente al rettangolo
R quindi, per la proprieta' transitiva dell'equivalenza, Q e' equivalente ad R come volevamo
In lettere scriveremo
AB2 = BH · BC
Teorema di Pitagora
E' forse il teorema piu' noto della geometria ma non e' quello
originale di Pitagora
In ogni triangolo rettangolo la somma dei quadrati costruiti sui
cateti e' equivalente al quadrato costruito sull'ipotenusa
Cioe' Q1 + Q2 equivalente a Q3
Nei problemi sara' particolarmente importante la seguente forma
del teorema
AB2 + AC2= BC2
Poiche' tale formula coinvolge 3 quantita' sara' sufficiente
conoscerne 2 per trovare la terza
Passiamo alla dimostrazione
ipotesi
BAC triangolo
rettangolo
tesi
Q +Q
1
equivalente a
2
Q
3
Prolungo l'altezza AH, in tal modo il quadrato Q3 venga suddiviso nei rettangoli R1 e R2
Per il primo teorema di Euclide Q1 e' equivalente a R1
per il primo teorema di Euclide Q2 e' equivalente a R2
quindi Q1 + Q2 equivalente a R1 + R2 = Q3
come volevamo
In lettere scriveremo
BC2 = AB2 + AC2
http://www.ripmat.it/piano.html
Secondo teorema di Euclide
In ogni triangolo rettangolo il quadrato costruito
sull'altezza relativa all'ipotenusa e' equivalente al
rettangolo che ha per lati le proiezioni dei cateti
sull'ipotenusa
Nei problemi sara' particolarmente importante la
seguente forma del teorema
AH2 = BH ·HC
Poiche' tale formula coinvolge 3 quantita' sara'
sufficiente conoscerne 2 per trovare la terza
Passiamo alla dimostrazione
ipotesi
BAC triangolo rettangolo
tesi
Q
2
equivalente a
R
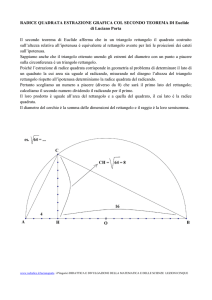
In questo teorema la cosa piu' difficile e' fare la figura
come si costruisce la figura:
costruisco il quadrato sul lato AB; costruisco il quadrato sull'altezza AH
siccome mi serve il rettangolo di lati BH ed HC considero il rettangolo di lati BH e BC (come nella
figura del primo teorema di Euclide) e poi tolgo il
quadrato di lato BH
Per il primo teorema di Euclide ho che
Q1 equivalente Q3 + R
Per il teorema di Pitagora ho che
Q1 equivalente a Q2 + Q3
per la proprieta' transitiva dell'equivalenza avro'
Q3 + R equivalente Q2 + Q3
Togliendo Q3 da entrame le parti dell'equivalenza
otteniamo
R equivalente a Q2
come volevamo dimostrare
In lettere scriveremo
AH2 = BH · HC