s_040716

STATISTICA E MISURAZIONE
venerdì 16 luglio 2004
Prof. Cesare Svelto
Tempo a disposizione 2 ore e 30 minuti
Secondo Appello AA 2003/2004
Aula V.S.9 ore 9.15
Cognome e nome: __________________________
_____________________
(stampatello)
Matricola e firma __ __ __ __ __ __
_____________________ (firma leggibile)
Esercizi svolti (almeno parzialmente): 1 2 3 4 5
(crocettare)
N.B. gli esercizi non crocettati non saranno corretti; quelli crocettati ma neanche iniziati comporteranno una
penalità.
SOLUZIONI
Esercizio 1
(svolgere su questo foglio e sul retro)
1)
1a)
1b)
1c)
Per misurare la variabilità temperatura del mese di agosto a Milano, ogni 2 giorni viene acquisita la
temperatura media giornaliera, ottenendo questa serie di dati:
Temperatura (°C): 26, 28, 28, 25, 30, 26, 25, 28, 29, 22, 27, 28, 30, 26.
Calcolare la media e la varianza campionaria.
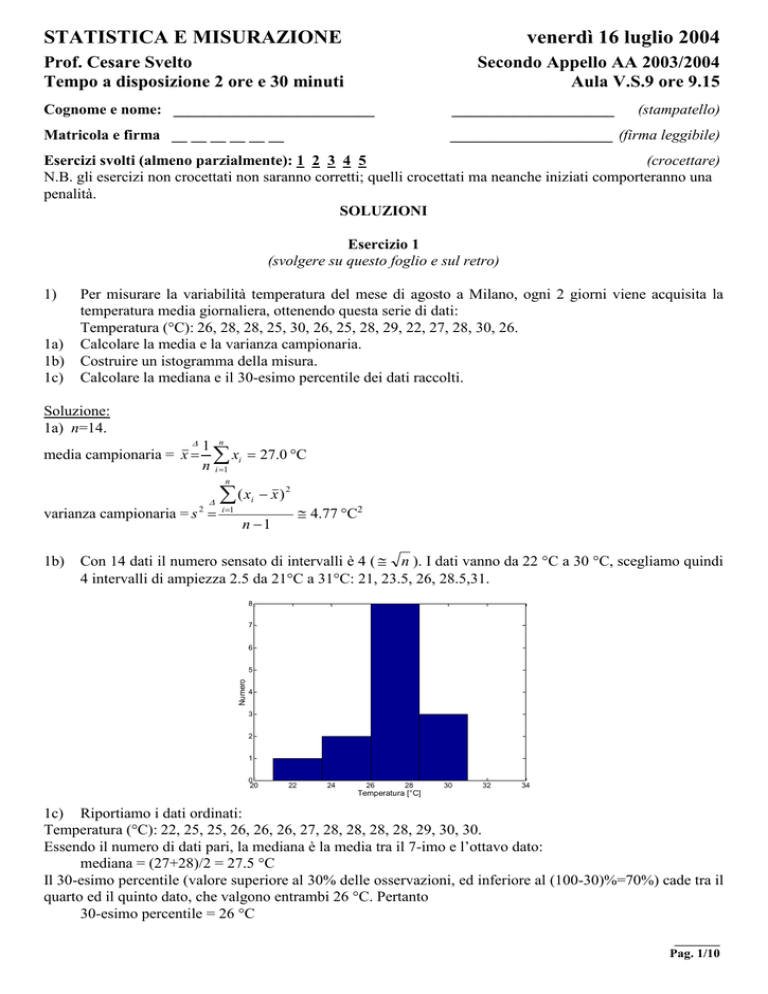
Costruire un istogramma della misura.
Calcolare la mediana e il 30-esimo percentile dei dati raccolti.
Soluzione:
1a) n=14.

media campionaria = x 
1 n
 xi  27.0 °C
n i 1
n

varianza campionaria = s 2 
1b)
 (x
i 1
i
 x)2
 4.77 °C2
n 1
Con 14 dati il numero sensato di intervalli è 4 (  n ). I dati vanno da 22 °C a 30 °C, scegliamo quindi
4 intervalli di ampiezza 2.5 da 21°C a 31°C: 21, 23.5, 26, 28.5,31.
8
7
6
Numero
5
4
3
2
1
0
20
22
24
26
28
30
32
34
Temperatura [°C]
1c) Riportiamo i dati ordinati:
Temperatura (°C): 22, 25, 25, 26, 26, 26, 27, 28, 28, 28, 28, 29, 30, 30.
Essendo il numero di dati pari, la mediana è la media tra il 7-imo e l’ottavo dato:
mediana = (27+28)/2 = 27.5 °C
Il 30-esimo percentile (valore superiore al 30% delle osservazioni, ed inferiore al (100-30)%=70%) cade tra il
quarto ed il quinto dato, che valgono entrambi 26 °C. Pertanto
30-esimo percentile = 26 °C
_______
Pag. 1/10
Esercizio 1
(continua
_______
Pag. 2/10
Esercizio 2
(svolgere su questo foglio e sul retro)
2)
2a)
2b)
2c)
Un nostro amico,proprietario di un negozio di abbigliamento, pone dei quesiti sulle probabilità che lui
incontra nella vita quotidiana.
Al suo negozio si presentano mediamente 5 clienti all’ora. Spiegando il tipo di distribuzione utilizzata
si calcoli la probabilità che in 30 minuti si presentino esattamente 3 clienti. Quanto vale invece la
probabilità che in 12 minuti si presenti almeno un cliente?
Statisticamente il 30 % dei clienti paga con carta bancomat, carta di credito o assegno. Su 10 clienti
quanto vale la probabilità che almeno 8 abbiano pagato in contanti?
L’incasso mensile, dipendendo da molte variabili, si può considerare a distribuzione gaussiana. Negli
ultimi mesi l’incasso medio è stato pari a 10˙000 euro con deviazione standard di 2˙000 euro. Quanto
vale la probabilità che il prossimo mese l’incasso sia superiore a 15˙000 euro?
Soluzione:
2a) Utilizziamo una distribuzione di probabilità poissoniana.
e   x
,
x  0,1,2...
La funzione di probabilità di una variabile poissoniana X vale f ( x) 
x!
il suo valor medio vale  =  e la sua varianza vale 2 = .
Tipicamente questa distribuzione di probabilità descrive il numero di eventi che avvengono casualmente in
un dato intervallo di tempo.
Il valor medio vale  = 5 clienti/ora ∙ 0.5 ore = 2.5 clienti.
La probabilità che in 30 minuti arrivino esattamente 3 clienti vale
e    x e 2.5 2.53
P( x  3) 

 0.2137  21.4%
x!
3!
La probabilità che arrivi almeno 1 cliente in 15 minuti è uguale a 1 meno la probabilità che non ne sia
arrivato nessuno (il valor medio vale  = 5 clienti/ora ∙ 0.2 ore = 1 cliente)
e   0
P( x  1)  1  P( x  0)  1 
 1  e   1  e 1  0.6321  63.21%
0!
2b) Dato che ogni prova è un processo di Bernoulli (o paga o non paga in contanti, ovvero successo o
insuccesso), le prove sono indipendenti e la probabilità di successo in ogni prova è costante, la probabilità di
x clienti che pagano in contati su n clienti segue la distribuzione binomiale, con probabilità di successo p =0.7
(=1- 30%):
n
10 
8
P(8 successi su 10 prove )    p x (1  p) nx   0.7  (0.3)108  0.233  23.3 %
 x
8
n
10  10! 10  9
n!
avendo ricordato che   
e dunque   
=45

 x  x!(n  x)!
 8  8!2! 2  1
Viene richiesta la probabilità che almeno 8 paghino in contanti che vale quindi:
P( x  8)  P( x  8)  P( x  9)  P( x  10)  0.233  0.121  0.028  0.382  38.2%
avendo calcolato le probabilità come descritto in precedenza.
_______
Pag. 3/10
Esercizio 2
(continua)
2c)
Per calcolare la probabilità standardizziamo la variabile casuale gaussiana, sapendo che
 = 10˙000 euro e  = 2˙000 euro, e ricorriamo quindi alla tabella dei valori della distribuzione cumulativa
x
(z) per una variabile normale standard (VNS). Ricordiamo che z 
è la VNS ricavata da x.

15000   
15000  10000 


P( x  15000)  P z 
  P z 
  P( z  2.5)  1  P( z  2.5) 

2000




 1   (2.5)  1  0.99379  0.621%
_______
Pag. 4/10
Esercizio 3
(svolgere su questo foglio e sul retro)
3) Per controllare la qualità di tubi d’acciaio prodotti da un’azienda, si intende verificare il diametro di un
particolare tubo per utilizzo alimentare, con diametro nominale pari a 6 mm. Acquistiamo quindi vari
spezzoni di tubo e ne misuriamo i diametri in più punti, ottenendo i seguenti valori:
D = 5.8, 5.9, 6.2, 6.1, 5.7, 6, 6, 5.6, 5.8, 5.9 [mm].
3a) Si dia una definizione di Potenza di un test statistico:
3b) Si effettui un test statistico con lo scopo di verificare se il diametro dei tubi prodotti è diverso dal
diametro nominale, con livello di significatività pari al 5 %
3c) Quanto vale il valore P del test effettuato?
Soluzione:
3a) La potenza di un test statistico è la probabilità di rifiutare l’ipotesi nulla quando questa è falsa. È uguale
a 1- la probabilità  di errore di tipo II:
Potenza = 1 -  = 1 - P(errore di tipo II) = 1 - P(accettare H0 quando H0 è falsa)
La potenza è un parametro che ci descrive la capacità del test di rivelare le differenze della realtà rispetto ad
H0.
3b) Si tratta di un test t, in quanto dobbiamo stimare il valor medio di una popolazione con varianza ignota. Il
numero di gradi di libertà  = n – 1 = 9. Calcoliamo il valor medio e la deviazione standard campionaria.

X
1 n
 X i  5.90 mm
n i 1
s X  
1 n
X k  X 2  0.1826 mm

n  1 k 1
Effettuiamo quindi un test t.
1. Il parametro di interesse è il diametro del tubo, che chiamiamo 
2. H0:  = 6 mm
3. H1:   6 mm (il test è a due lati, in quanto vogliamo controllare l’esattezza della dimensione del
tubo)
4. livello di significatività richiesto  = 0.05
5. La statistica di test è la statistica t: t 0 
X  X 

sX
s/ n
6. Rifiutiamo H0 se t0 > t/2,9 = 2.262 o se t0 < -t/2,9 = -2.262 (questo risultato si ricava dalla tabella dei
punti percentuale della distribuzione t, con  = 9 e /2 = 0.025)
7. Calcoliamo quindi t0, t 0 
X  X 
5.9  6


 1.73
sX
s / n 0.1826 / 10
8. Conclusione: non rifiutiamo l’ipotesi nulla con livello di significatività 0.05.
_______
Pag. 5/10
Esercizio 3
(continua)
3c) Il valore P, che corrisponde al livello di significatività di soglia tra l’accettazione ed il rifiuto di H0, si può
ricavare dalla tabella punti percentuale della distribuzione t, con  = 9 (data la simmetria della distribuzione
lavoriamo per valori positivi):
ZP/2 = Z/2 = 1.73. Il valore di /2 che si ricava è compreso tra 0.05 e 0.1, stimabile in 0.6, per cui il valore
P0.12.
L’interpretazione di questo valore è che l’ipotesi nulla sarebbe stata dichiarata falsa per qualsiasi livello di
significatività  maggiore del 12 %. In questo caso con  = 5 % non si è potuto rifiutare H0.
_______
Pag. 6/10
Esercizio 4
(svolgere su questo foglio e sul retro)
4) Sistema Internazionale di unità di misura (SI):
4a) Dire perché è un sistema coerente, quante e quali sono le sue unità di base.
4b) Riportate l’attuale definizione delle prime 4 unità di misura fondamentali (si ricordi MKSA…).
4c) Descrivete brevemente come queste 4 unità di misura si realizzano praticamente e indicate il livello di
accuratezza per ciascuno dei corrispondenti campioni primari.
4) Si vedano gli appunti e le dispense del corso.
_______
Pag. 7/10
Esercizio 4
(continua)
_______
Pag. 8/10
Esercizio 5
(svolgere su questo foglio e sul retro)
5) In un sistema di trasmissione wireless tra due PC il trasmettitore emette una potenza nominale pari a
20 mW, data dal costruttore come compresa tra 17 mW e 23 mW al 99,7 % di probabilità. L’attenuazione di
spazio libero tra i due PC può variare, nel caso considerato, tra un fattore 3 e un fattore 4. Il ricevitore ha
un’antenna con impedenza Z = 75  ± 5 %.
5a) Ricavare l’espressione e calcolare il valore della potenza ricevuta Pric (in watt e in dBm) e la sua
incertezza tipo.
5b) Ricavare l’espressione e calcolare il valore della tensione efficace che si sviluppa sull’antenna e la sua
incertezza relativa.
5c) Il segnale rivelato dall’antenna viene quindi amplificato di 20 dB da un amplificatore e inviato a 2
circuiti connessi in parallelo, con resistenze di ingresso R1 = 10 k e R2 = 11 k misurati con un ohmetro a 3
cifre con fondo scala di 1 M. Calcolare la corrente erogata dall’amplificatore e le sua incertezza tipo.
5a) La potenza trasmessa PT ha valor medio pari a 20 mW e incertezza estesa con fattore di copertura 3 pari a
3 mW (deriva del 99,7 %, che è la probabilità racchiusa da 3).
Per cui la sua incertezza tipo vale u(PT) =1 mW:
PT = 20 ± 1 mW
L’incertezza relativa vale uR(PT)=1/20= 5 %
L’attenuazione di spazio libero A segue una distribuzione uniforme di valori centrata in 3.5 e di larghezza 1,
per cui la sua incertezza vale u ( A)  1 / 12  0.29 .
A  3.5  0.29
L’incertezza relativa vale uR(A)=0.29/3.5  8.3 %
La potenza ricevuta ricevuta vale
PRIC  PT / A = 20/3.5 mW  5.714 mW che corrisponde a 7.57 dBm.
Essendo una produttoria ad esponenti con modulo unitario, l’incertezza relativa si ottiene come somma
quadratica delle incertezze relative:
u R ( PRIC )  u R ( PT )  u R ( A)  0.052  0.0832  9.7 %
Quindi la sua incertezza tipo vale u(PRIC)= PRIC  uR(PRIC)  0.55 mW
PRIC = 5.71 ± 0.55 mW
2
2
5b) La tensione efficace che si sviluppa sull’antenna vale
V A  PRIC Z  0.42825 V  0.6544 V
La sua incertezza relativa si può calcolare come somma quadratica delle incertezze relative moltiplicate per
gli esponenti al quadrato della produttoria (oppure si può calcolare dalla formula generale con i coefficienti di
sensibilità; questo è solo un caso particolare):
u R (V A ) 
1
4
u R ( PRIC )  14 u R ( Z )  0.00235  0.000625  5.5 %
2
2
5c) La tensione in uscita dall’amplificatore vale:
VOUT  V A  10  6.54 V
L’incertezza relativa della tensione dopo l’amplificatore resta la stessa, mentre l’incertezza tipo aumenta di
20 dB (fattore 10 in ampiezza).
u(VOUT)= VOUT  uR(VOUT)  0.36 V
Le due resistenze sono state misurate con un ohmetro che ha risoluzione di 1 k, per cui hanno un’incertezza
di quantizzazione pari a u ( R)  1 kΩ / 12  0.29 kΩ
_______
Pag. 9/10
Esercizio 5
(continua)
Queste incertezze sono scorrelate, in quanto l’ohmetro è supposto ideale, quindi senza polarizzazioni o errori
di scala (ogni quantizzazione è indipendente).
La corrente erogata dall’amplificatore vale:
V
V
I  OUT  OUT
R1 // R2
RP
dove
RR
RP  R1 // R2  1 2  5.238 kΩ
R1  R2
u  RP  

2
2
 RP  2
 RP  2

 u R1   
 u  R2  

R

R
 1
 2
2
2
 R2 2
 2
 R1 2
 2
u R1   
u  R2  

2 
2 




R

R
R

R
2
2
 1

 1

0.063  0.043 kΩ  0.33 kΩ
Che corrisponde ad un’incertezza relativa
uR(RP)=0.33/5.24  6.3 %
Calcoliamo quindi la corrente erogata e la sua incertezza relativa (come somma quadratica delle incertezze
relative di VOUT e RP):
V
V
6.54
I  OUT  OUT 
mA  1.25 mA
R1 // R2
RP
5.24
u R ( I )  u R (VOUT )  u R ( RP )  0.055 2  0.0632  8.4 %
2
2
Da cui
u(I)= I  uR(I)  0.10 mA
_______
Pag. 10/10